Лабораторно-практическая работа № 8 - Расчетно-графическая работа (Вариант 20)

Федеральное государственное бюджетное образовательное учреждение

высшего профессионального образования

«Петербургский государственный университет путей сообщения

Императора Александра I»

Кафедра «Высшая математика»

Лабораторно-практическая работа № 8

Расчетно-графическая работа

Вариант 20

Выполнил: студент

факультета ТЭС

группы ПТМ-014

Васечкин А.А.

Проверил: профессор

Боровских Ю.В.

Санкт-Петербург

2023

Вариант 20

1. Условие задачи:

Склад железнодорожной станции имеет три электропогрузчика. Грузопоток погрузки пакетов грузов в вагоны – простейший с параметром λ = 7 пак./мин. Время погрузки одного пакета распределено по показательному закону, причем среднее время погрузки одного пакета равно 25 сек. На погрузочном участке имеется накопитель, позволяющий держать в очереди на погрузку четыре пакета. Если в момент поступления грузового пакета со склада все погрузчики и места на накопителе заняты, то пакет не нагружается в вагоны по этой технологии. Если есть хотя бы одно свободное место на контейнере-накопителе, то пакет ожидает на нем в очереди момента погрузки.

2. Кодировка Кендалла для данной СМО:

Открытая СМО M|M|3ǀ4

λ=7

μ=2.4

m=3

n=4

3. Формулы для распределений интервалов во входном потоке и длительностей обслуживания:

Распределение интервалов во входном потоке (показательное распределение):

Распределение длительности обслуживания (показательное распределение):

4. Диаграмма интенсивностей переходов между состояниями:

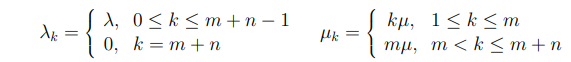
Многоканальная СМО с ограниченной очередью

λ

λ

λ

0

m=3

2

1

3µ

2µ

µ

5. Система дифференциальных уравнений Колмогорова для определения вероятностей состояний СМО в произвольный момент времени:

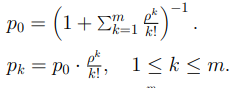
6. Проверка условий наличия стационарного решения:

Стационарный режим СМО M|M|m|n существует при любых условиях

7. Система уравнений для определения стационарных вероятностей состояний

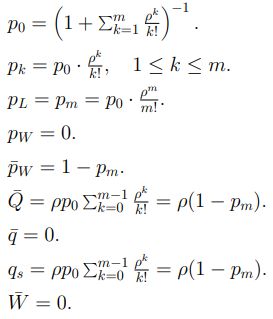
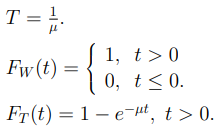
8. Решение системы п. 7, т.е. стационарные вероятности состояний СМО

Для наших значений:

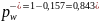
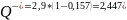
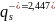
9. Основные показатели эффективности работы СМО, вычисленные с помощью средств системы Matlab:

>> lambda=0.2; mu=0.1; m=3; n=4;

rho=lambda/mu;

rho_m=rho/m;

N=m+n;

x=1:N;

x1=ones(1,N)*m;

xx=min(x,x1);

slave1=ones(1,N)*rho;

slave2=slave1./xx;

slave=cumprod(slave2);

disp('Вероятность простоя системы');

P0=1/(1+sum(slave));

disp(P0);

disp('Вероятности состояний 1,...,N');

Psost=slave*P0;

disp(Psost);

disp('Вероятность потери требования');

Potk=Psost(N);

disp(Potk);

disp('Вероятность ожидания перед обслуживанием');

Pw=0;

disp(Pw);

disp('Вероятность обслуживания без ожидания');

Pww=1-Psost(m);

disp(Pww);

disp('Среднее число заявок в системе');

Qsr=(1:N)*Psost';

disp(Qsr);

xx1=x-x1;

disp('Среднее число заявок в очереди');

qsr=0;

disp(qsr);

disp('Среднее число занятых приборов');

qs=xx*Psost';

disp(qs);

disp('Среднее время ожидания');

W=0;

disp(W);

disp('Среднее время пребывания в системе');

T=W+1/mu;

disp(T);

>> Num=input('Число изменений состояния системы за время моделирования ');

Число изменений состояния системы за время моделирования 100

>> N=m+1;

s=1;

T=zeros(1,Num);

Qt=zeros(1,Num);

Time=zeros(1,N);

for i=2:Num

switch Qt(i-1)

case 0

v=Inf; u=-log(rand)/lambda;

case m+n

u=Inf; v=-log(rand)/(m*mu);

otherwise

u=-log(rand)/lambda;

qs=min(m,Qt(i-1));

v=-log(rand)/(qs*mu);

end;

delta_time=min(u,v);

T(i)=T(i-1)+delta_time;

Time(s)=Time(s)+delta_time;

if u<v

Qt(i)=Qt(i-1)+1;

else

Qt(i)=Qt(i-1)-1;

end

s=Qt(i)+1;

end;

z=zeros(1,Num);

mvect=ones(1,Num)*m;

qt=max(z,Qt-mvect);

subplot(211); plot(T,Qt);

subplot(212); plot(T,qt);

Результаты моделирования:

- Показатели эффективности, полученные на основе результатов моделирования и стационарные вероятности состояний СМО:

Вероятность простоя системы

0.0361

Вероятности состояний 1,...,N

0.1052 0.1534 0.1491 0.1450 0.1410 0.1370 0.1332

Вероятность потери требования

0.1332

Вероятность ожидания перед обслуживанием

0

Вероятность обслуживания без ожидания

0.8509

Среднее число заявок в системе

2.5281

Среднее число заявок в очереди

0

Среднее число занятых приборов

2.5281

Среднее время ожидания

0

Среднее время пребывания в системе

0.4167

- График числа клиентов в СМО (сверху) и график числа клиентов в очереди (снизу)

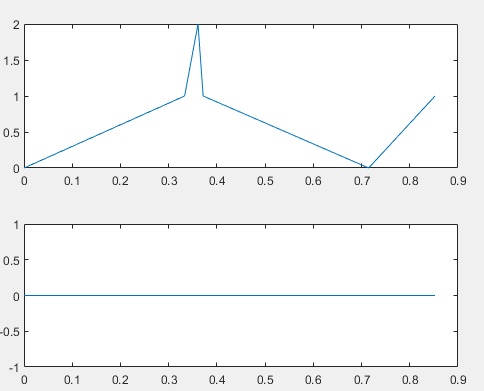
10. Сравнение полученных результатов, выводы:

	Ручной	Matlab
Вероятность простоя	0,0388	0.0361
Вероятность потери требования	0,157	0.1332
Вероятность ожидания перед обслуживанием	0	0
Вероятность обслуживания без ожидания	0,843	0.8509
Среднее число заявок в системе	2,447	2.5281
Среднее число заявок в очереди	0	0
Среднее число занятых приборов	2,447	2.5281
Среднее время ожидания	0	0
Среднее время пребывания в системе	0,42	0,4167

Проведен анализ работы Марковской СМО. Вычислены основные показатели эффективности работы СМО. Проводился как теоретический, так и статистический расчет, основанный на моделировании. Расчётные результаты и результаты моделирования совпадают в пределах погрешностей, определяемых статистическим характером расчѐтов, что говорит о возможности практического применения для расчетов характеристик СМО этих двух способов.