Лабораторно-практическая работа № 5 - Построение минимального остова с помощью алгоритма Прима
.docxФедеральное государственное бюджетное образовательное учреждение
высшего профессионального образования
«Петербургский государственный университет путей сообщения
Императора Александра I»
Кафедра «Высшая математика»
Лабораторно-практическая работа № 5
по дисциплине «Математическое моделирование
систем и процессов»
Построение минимального остова с помощью алгоритма Прима.
Вариант 20
Выполнил: Васечкин А. А.
факультета ТЭС
группы ПТМ-014
****************.
Проверил: профессор
Боровских Ю.В.
Санкт-Петербург
2023
Задание:
Изобразить
в виде рисунков ориентированную сеть
,
заданную весовой матрицей
.
Построить минимальный остов для сети
с помощью алгоритма Прима.
Исходные данные:
W3=
Решение:
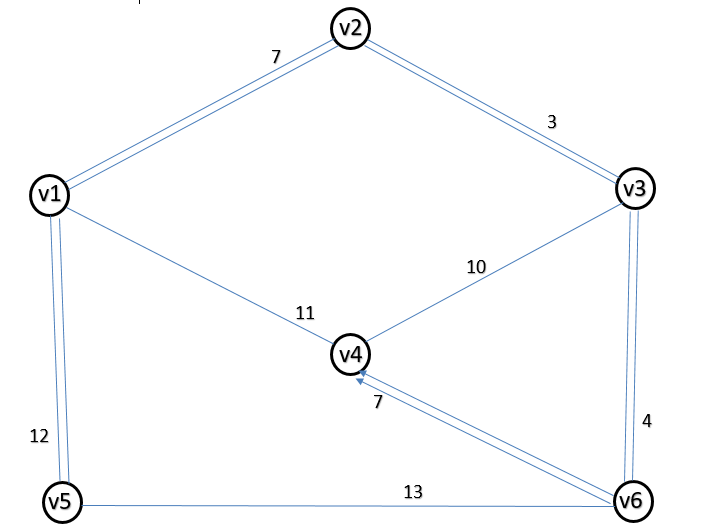
Построение графа
13
14
10
4
3
12
11
7
v6
v5
v3
v1
7
v4
v2
Шаг 0 – Берем любую вершину графа v ϵ V:
v2 ϵ V
V’ = {v2}
V’’ = V \ v2 = {v1, v3, v4, v5, v6}
E’ = Ø
Шаг 1 – Определяем в разрезе ребро с минимальным весом: (1-я итерация)
E(V’, V’’) = {[v2, v1], [v2, v3]}
e* = [v2, v3]
w(e*) = 3
Шаг 2 – Обновляем граф и подграф:
V’new = {v2, v3}
V’’new = {v1, v4, v5, v6}
E’new = {[v2, v3]}
Шаг 3 – проверка на завершение алгоритма:
#E’ ≠ 5, переходим к шагу 1
Шаг 1: (2-я итерация)
E(V’, V’’) = {[v2, v1], [v3, v4], [v3, v6]}
e* = [v3, v6]
w(e*) = 4
Шаг 2:
V’new = {v2, v3, v6}
V’’new = {v1, v4, v5}
E’new = {[v2, v3], [v3, v6]}
Шаг 3:
#E’ ≠ 5, переходим к шагу 1
Шаг 1: (3-я итерация)
E(V’, V’’) = {[v2, v1], [v3, v4], [v6, v4], [v6, v5]}
e* = [v6, v4]
w(e*) = 7
Шаг 2:
V’new = {v2, v3, v4, v6}
V’’new = {v1, v5}
E’new = {[v2, v3], [v3, v6], [v6, v4]}
Шаг 3:
#E’ ≠ 5, переходим к шагу 1
Шаг 1: (4-я итерация)
E(V’, V’’) = {[v1, v2], [v3, v4], [v1, v4], [v4, v3], [v4, v6]}
e* = [v1, v2]
w(e*) = 7
Шаг 2:
V’new = {v1, v2, v3, v4, v6}
V’’new = {v5}
E’new = {[v2, v3], [v3, v6], [v6, v4], [v1, v2]}
Шаг 3:
#E’ ≠ 5, переходим к шагу 1
Шаг 1: (5-я итерация)
E(V’, V’’) = {[v3, v4], [v1, v4], [v1, v5], [v4, v6], [v5, v6]}
e* = [v1, v5]
w(e*) = 12
Шаг 2:
V’new = {v1, v2, v3, v4, v5, v6}
V’’new = Ø
E’new = {[v2, v3], [v3, v6], [v6, v4], [v1, v2], [v1, v5]}
Шаг 3:
#E’ = 5, алгоритм завершен
Ответ: цена минимального пути 33
