
МИНОБРНАУКИ РОССИИ
Санкт-Петербургский государственный
электротехнический университет
«ЛЭТИ» им. В.И. Ульянова (Ленина)
Кафедра физика
отчет
по лабораторной работе №5
по дисциплине «Физика»
Тема: «Исследование электростатического поля двухпроводной линии методом моделирования»
Студент гр. 1282 |
|
SEMEN KOZLOV. |
Преподаватель |
|
Мамыкин А.И. |
Санкт-Петербург
2021
Лабораторная работа №5
ИССЛЕДОВАНИЕ ЭЛЕКТРОСТАТИЧЕСКОГО ПОЛЯ
ДВУХПРОВОДНОЙ ЛИНИИ МЕТОДОМ МОДЕЛИРОВАНИЯ
ЦЕЛЬ РАБОТЫ
Ознакомление с методикой моделирования электростатического поля в токопроводящей среде; исследование электростатического поля, созданного системой из проводящих тел.
 ЭСКИЗ
ИЛИ СХЕМА УСТАНОВКИ
ЭСКИЗ
ИЛИ СХЕМА УСТАНОВКИ
Лабораторный макет установки для моделирования электростатического поля (рис. 5.1). В работе используется планшет 1, покрытый проводящей бумагой, с нанесенными на него металлическими электродами 2. На планшете установлены две подвижные линейки 3, с помощью которых определяются координаты щупа 4, подключенного к вольтметру PV. Помещая щуп в различные точки планшета и измеряя потенциал данной точки, можно построить картину исследуемого поля.
ОСНОВНЫЕ РАСЧЕТНЫЕ ФОРМУЛЫ
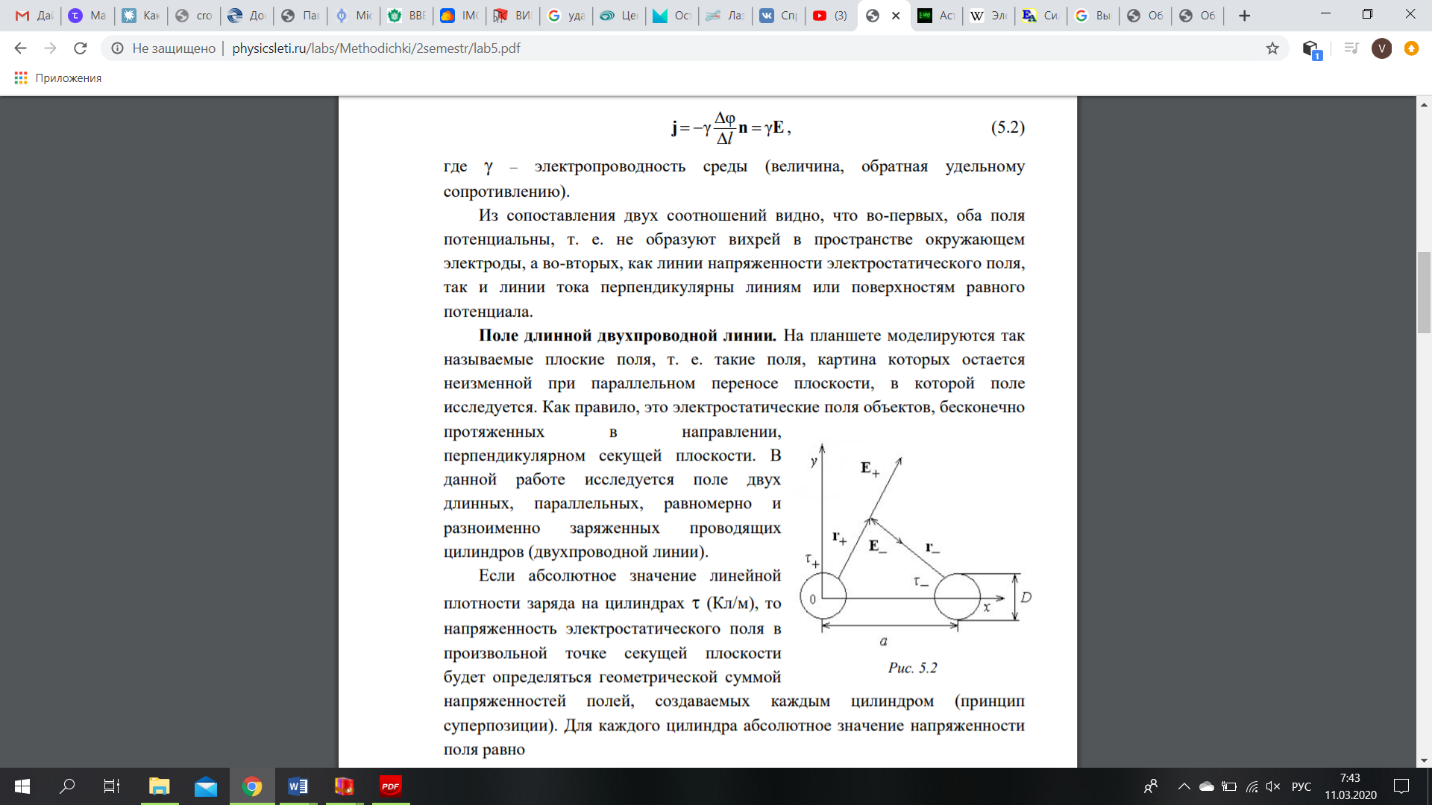 1)
Абсолютное
значение напряженности поля для цилиндра.
1)
Абсолютное
значение напряженности поля для цилиндра.

где - абсолютное значение линейной плотности заряда на цилиндрах
2) Напряженность электростатического поля в произвольной точке секущей плоскости определяется геометрической суммой напряженностей полей, создаваемых каждым цилиндром (принцип суперпозиции), а значение и направление результирующего вектора напряженности поля определяют по отношению к системе координат x0y (рис. 5.2), которую задает экспериментатор.
3) Соотношение между энергетической и силовой характеристиками поля для электростатического поля.
![]()
4) Проекции вектора напряжённости на оси декартовой системы координат.
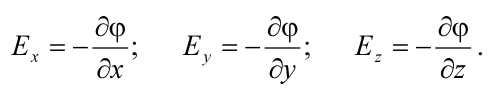
5) Соотношение между энергетической и силовой характеристиками поля для электростатического поля через физический смысл градиента.
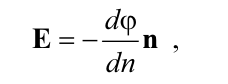
где n – единичный вектор соответствующего направления.
6) Приближенное значение проекции напряженности в некоторой точке по измеренным значениям потенциала вблизи этой точки.
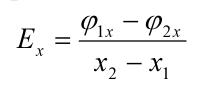
где в числителе указана разность потенциалов, измеренных в точках с соответствующими координатами, а в знаменателе разность координат этих точек.
ПРОТОКОЛ НАБЛЮДЕНИЙ
К ЛАБОРАТОРНОЙ РАБОТЕ №5
«ИССЛЕДОВАНИЕ ЭЛЕКТРОСТАТИЧЕСКОГО ПОЛЯ ДВУХПРОВОДНОЙ ЛИНИИ МЕТОДОМ МОДЕЛИРОВАНИЯ»
табл. 1
№ |
1 |
2 |
x, см |
9,2 |
30,2 |
y, см |
14,5 |
14,5 |
φ, В |
0 |
12,7 |
θl = 0,05 см
θφ = 0,05 В
№ |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
x, см |
10 |
12 |
14 |
16 |
18 |
20 |
22 |
24 |
26 |
28 |
y, см |
14,5 |
14,5 |
14,5 |
14,5 |
14,5 |
14,5 |
14,5 |
14,5 |
14,5 |
14,5 |
φ, В |
0,61 |
1,54 |
3,27 |
4,51 |
5,5 |
6,52 |
7,74 |
8,44 |
8,59 |
11,46 |
табл.2
№ |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
x, см |
0 |
2 |
4 |
6 |
8 |
32 |
34 |
36 |
38 |
40 |
y, см |
14,5 |
14,5 |
14,5 |
14,5 |
14,5 |
14,5 |
14,5 |
14,5 |
14,5 |
14,5 |
φ, В |
2,02 |
1,91 |
1,7 |
1,16 |
0,18 |
12,42 |
11,44 |
10,93 |
10,7 |
10,61 |
табл.3 табл.4
№ |
1 |
2 |
3 |
x, см |
3 |
3,5 |
3 |
y, см |
8 |
8 |
7,5 |
φ, В |
2,5 |
2,5 |
2,6 |
№ |
1 |
2 |
3 |
x, см |
15 |
15 |
15,5 |
y, см |
22 |
21,5 |
22 |
φ, В |
4,7 |
4,8 |
4,9 |
№ |
1 |
2 |
3 |
x, см |
23,5 |
24 |
24 |
y, см |
8 |
8 |
7,5 |
φ, В |
7,7 |
8 |
7,9 |
табл.5 табл.6
№ |
1 |
2 |
3 |
x, см |
35,5 |
36 |
36 |
y, см |
22 |
22 |
21,5 |
φ, В |
9,95 |
10 |
10,1 |
ОБРАБОТКА РЕЗУЛЬТАТОВ
1. По формуле рассчитаем экспериментальные значения напряженности поля в точках, расположенных вдоль линии, соединяющей электроды, и внесем значения в табл.7. Нанесем на график ход (1) изменения напряженности электрического поля вдоль этой линии (только экспериментальные точки).
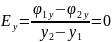
 =>
=>
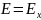
табл.7
E12
,
|
8,0 |
E13 , |
18,75 |
E14 , |
38,0 |
|
|
E2 , |
-66,5 |
E3 , |
-111,21 |
E4 , |
-55,75 |
E5 , |
-50,25 |
E6 , |
-56,0 |
E7 , |
-48,0 |
E8 , |
-21,25 |
E9 , |
-75,5 |
|
|
E17 , |
37,25 |
E18 , |
18,5 |
E19 , |
8,0 |
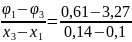 = -66,5 (
)
= -66,5 (
)
2. Считая диэлектрическую проницаемость моделируемой области = 1, определим по значению напряженности в одной из точек на линии между электродами моделируемый заряд (линейную плотность).
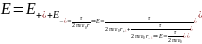

 , где τ
– моделируемый
заряд,
, где τ
– моделируемый
заряд,
x – расстояние от электрода до этой точки,
 d
– расстояние между электродами.
d
– расстояние между электродами.
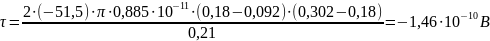
Рассчитаем, внесём в табл. 8 и нанесем на график с экспериментальными точками теоретические кривые (2) изменения напряженности электрического поля вдоль линии, соединяющей центры электродов.
табл.8
E1 , |
-145 |
E2 , |
-81 |
E3 , |
-61,3 |
E4 , |
-53 |
E5 , |
-50,1 |
E6 , |
-51 |
E7 , |
-56,3 |
E8 , |
-68,9 |
E9 , |
-102,1 |
E10 , |
-275,7 |
E11 , |
-55,5 |
E12 , |
-67,1 |
E13 , |
-96,7 |



E14 , |
-22,6 |
E15 , |
-20,8 |
E16 , |
-19,4 |

3. Определим и внесем в табл. 9 экспериментальные значения проекций на оси координат и модули напряженности поля в точках в остальных опытах.
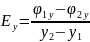
табл.9
i |
|
|
|
1’ |
0 |
14 |
14 |
2’ |
-38 |
6 |
20,39 |
3’ |
-50 |
-12 |
63,25 |
4’ |
-10 |
18 |
22,3 |
 =
=
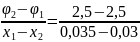 = 0
= 0
 =
=

E1’
=
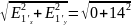 =14
=14
5. Рассчитаем для выбранных векторов напряженности погрешности их модулей, запишем полученные результаты в стандартном виде в табл.10 и на эскизе, рядом с соответствующим вектором.
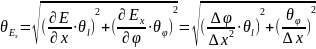

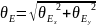

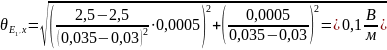


табл.10
i |
Ei , В/м |
|
|
2 |
-66,5 |
0,8 |
-66,5 |
3 |
-111,21 |
0,93 |
|
4 |
-55,75 |
0,70 |
|
5 |
-50,25 |
0,63 |
|
6 |
-56,0 |
0,7 |
|
7 |
-48,0 |
0,6 |
|
8 |
-21,25 |
0,27 |
|
9 |
-75,5 |
0,95 |
|
|
|
|
|
1’ |
14,0 |
2 |
14 2 |
2’ |
20,39 |
4,47 |
20,39 4,46 |
3’ |
63,25 |
6,35 |
|
4’ |
22,3 |
2,23 |
22,3 2,2 |
ВЫВОД
В ходе лабораторной работы было рассчитано напряжение по экспериментальным и теоретическим формулам. Сравнение значений было отображено на графике. Также были построены изображения некоторых векторов напряженности данного поля на эскизе модели установки. Через них были проведены схематические линии напряженности. Подтвердилось, что данные формулы справедливы не только для электростатического поля, но и для поля электрического тока в проводящей среде.



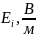
 , В/м
, В/м (В/м)
(В/м) 0,8
0,8 0,93
0,93 0,70
0,70 0,63
0,63 0,7
0,7 0,6
0,6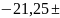 0,27
0,27 0,1
0,1 6,35
6,35