ЦЕЛЬ РАБОТЫ

Изучение методов обработки результатов прямых многократных независимых измерений и определение доверительных границ случайной погрешности.

ЗАДАНИЯ К РАБОТЕ

1. Произвести многократные независимые измерения.

2. Определить статистические оценки числовых вероятностных характеристик. Сделать вывод о состоятельности, несмещенности и эффективности полученных оценок.

3. Выявить и исключить грубые погрешности.

4. Построить кумулятивную линию, полигон и гистограмму по результатам измерений. Определить моду и медиану выборки.

5. Проверить гипотезу о нормальности распределения результатов измерений.

6. Определить доверительные границы случайной погрешности

ПРИБОРЫ И ОБОРУДОВАНИЕ

Мультиметр RLC измеритель E7- 22, набор резисторов ОМЛТ- 2 номиналом 180 Ом ± 10%.

ЭКСПЕРИМЕНТАЛЬНАЯ ЧАСТЬ

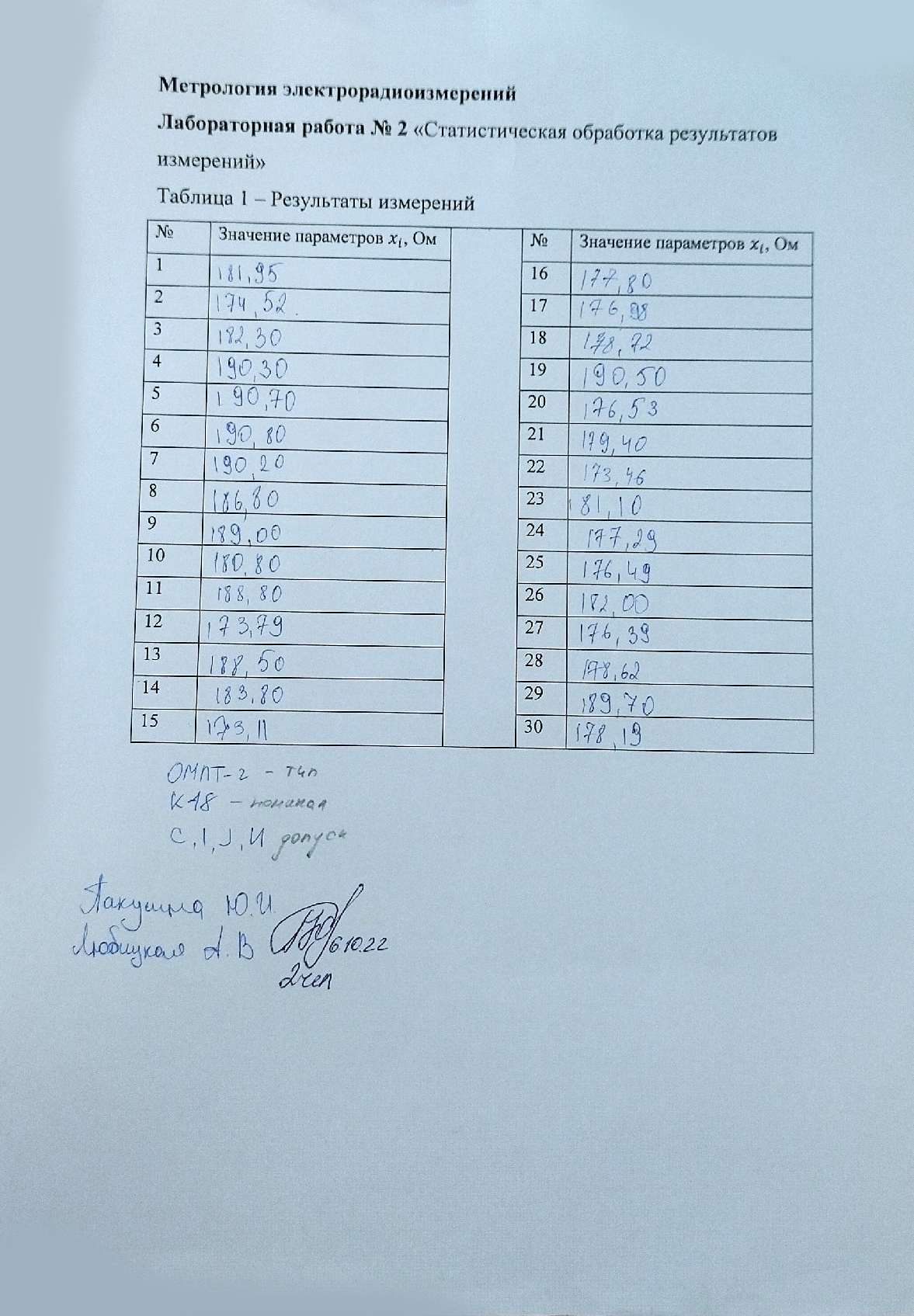
Результаты измерений представлены в таблице 1

Таблица 1 – Результаты измерений и расчетов

№	Значение параметров , Ом	Значение ранжированных по возрастанию параметров , Ом	, Ом
1	182,0	173,1	- 8,9
2	174,5	173,5	-8,5
3	182,3	173,8	-8,2
4	190,3	174,5	-7,5
5	190,7	176,4	-5,6
6	190,8	176,5	-5,5
7	190,2	176,5	-5,5
8	186,8	177,0	-5
9	189,0	177,3	-4,7
10	180,8	177,8	-4,2
11	188,8	178,2	-3,8
12	173,8	178,6	-3,4
13	188,5	178,7	-3,3
14	183,8	179,4	-2,6
15	173,1	180,8	-1,2
16	177,8	181,1	-0,9
17	177,0	182,0	0
18	178,7	182,0	0
19	190,5	182,3	0,3
20	176,5	183,8	1,8
21	179,4	186,8	4,8
22	173,5	188,5	6,5
23	181,1	188,8	6,8
24	177,3	189,0	7
25	176,5	189,7	7,7
26	182,0	190,2	8,2
27	176,4	190,3	8,3
28	178,6	190,5	8,5
29	189,7	190,7	8,7
30	178,2	190,8	8,8

Оценка начального момента первого порядка (математическое ожидание, среднее арифметическое, выборочное среднее значение) характеризует положение центра распределения:

Используя , можно найти отклонение каждого результата от среднего:

= -8,92 Ом

Оценка среднего квадратического отклонения (СКО) характеризует степень рассеивания сопротивления

Ом

Несмещенная оценка среднего квадратического отклонения результатов измерений

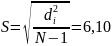Ом

Оценка центрального момента 3-го порядка характеризует ассиметрию распределения:

Согласно вычислениям наблюдается правосторонняя асимметрия.

Классификацию распределений по степени их протяженности можно осуществлять с помощью оценки коэффициента эксцесса.

Коэффициент эксцесса характеризует, что имеющееся распределение менее протяженное, чем нормальное распределение.

Статистическая оценка выборки представлена в таблице 2.

Таблица 2 – Статистические оценки выборки

, Ом	, Ом	, Ом	,
182,0	5,95	6,10	44,28	-1,39

Для исключения грубых погрешностей измерений (промахов) применяется критерий Граббса. В случаи, если имеются грубые промахи, исключается маловероятное значение и все вышеперечисленные расчеты повторяются. В случаи отсутствия грубых промахов вычисления продолжаются дальше.

Расчеты для применения критерия Граббса:

Уровень значимости q выбран свыше 5%. По результатам сравнения G1 и G2 с теоретическим значением GТ критерия Граббса при выбранном уровне значимости q (таблица 3) можно сделать вывод, что грубые промахи не считаются промахами и сохраняются в ряду результатов измерений, так как < , и < .

Таблица 3 – Критерий Граббса

1,44	1,51	2,876

Для построения полигона и гистограммы на основе экспериментальных данных необходимо разбить диапазон изменения значений случайной величины на равные интервалы. Количество интервалов можно вычислить по следующему правилу:

6

Длина интервалов находится как разность между максимальным и минимальным значениями измеренной величины деленная на K

Промежуточные расчеты для построения полигона, гистограммы и кумулятивной линии представлены в таблице 4.

Таблица 4 – Промежуточные расчеты

№ интервала	1	2	3	4	5	6
min значение интервала	173,1	176,1	179,0	181,9	184,9	187,8
max значение интервала	176,1	179,0	181,9	184,9	187,8	190,8
количество значений, попавших в заданный интервал	4	9	3	4	1	9

Полигон и гистограмма, построенные по результатам измерений, представлены на рисунке 1.

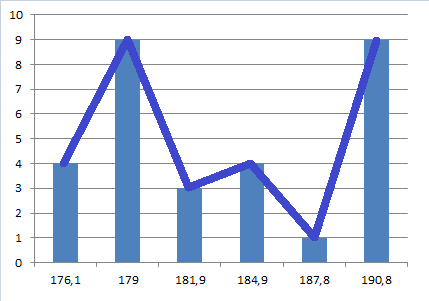
Рисунок 1 – График полигона и гистограммы

Кумулятивная линия по результатам измерений представлена на рисунке 2.

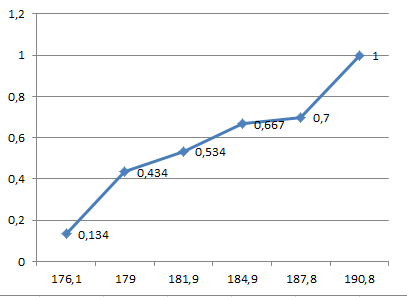
Рисунок 2 – Кумулятивная линия

Мода выборки – любое значение, вероятность которого больше, чем вероятность соседних значений.

182,0

Медиана выборки – это такое число, что вероятность поучить значение случайной величины справа от него равна вероятности получить значение слева от него.

180,9

Для проверки гипотезы о нормальности распределения результатов измерения будет применен составной критерий (таблица 4). По критерию 1 необходимо вычислить оценку среднего квадратического отклонения. Далее рассчитать

0,784

Уровень значимости принят равным 1%. Результаты измерений в ряду принадлежат нормальному распределению, так как выполняется условие .

Согласно критерию 2

2,58*6,10=15,74

Результаты измерений принадлежат нормальному, так как не более n = 30 разностей превысили значение .

Таблица 4 – Составной критерий

			P
0,784	0,8901	0,7040	0,99	2,58	15,74

В результате подтверждения гипотезы о нормальности распределения результатов измерений рассчитаны доверительные границы случайной погрешности:

ВЫВОД

Проанализированная выборка имеет правостороннюю асимметрию, большую протяженность по сравнению с нормальным распределением, принадлежит к нормальному распределению и имеет доверительные границы случайной погрешности 3,1 Ом