
Пособие_ТКИ
.pdfпредыдущие строки таблицы. Соответствующий син-
дром |
Sj = еjНт запишем в первый (крайний левый) |
столбец |
j-ой строки. В оставшиеся 2k ячеек этой строки |
запишем суммы еj и содержимого первой строки (т.е. кодового слова).
3. Повторяем шаг 2 процедуры, пока все вектора из V2 не окажутся включенными в таблицу. Эквивалентно, повторяем шаг 2 пока j<2n-k, иначе Стоп.
Пример 5. Стандартная таблица двоичного линейного
(4,2,2) кода:
S |
00 |
01 |
10 |
11 |
00 |
0000 |
0110 |
1011 |
1101 |
11 |
1000 |
1110 |
0011 |
0101 |
10 |
0100 |
0010 |
1111 |
1001 |
01 |
0001 |
0111 |
1010 |
1100 |
Декодирование с помощью стандартной таблицы выполняется следующим образом. Пусть r=v+е принятое слово. Найдем это слово в таблице и возьмем в качестве результата декодирования сообщение u, записанное в верхней (первой) ячейке того столбца, в котором лежит принятое слово r. По идее, этот процесс требует хранения в памяти всей таблицы и поиска в ней заданного слова.
Однако, возможно некоторое упрощение процедуры декодирования, если заметить, что все элементы одной и той же строки имеют один и тот же синдром. Каждая строка Rowi, 0< i <2n-k, этой таблицы представляет смежный класс кода С, а именно, Rowi = {еi+v|v С}. Вектор е, называется ли-
дером смежного класса.
Синдром всех элементов i-ой строки равен |
|
si =(ei+v)∙HT =еiНT |
(4.3.1.9) |
61
и не зависит от конкретного значения кодового слова v С. Упрощенная процедура декодирования состоит в следующем: вычислить синдром принятого слова r = еj + v
Sj = (ej+v)HT = еjНT
и найти его в левом столбце стандартной таблице; взять лидер смежного класса е'j из второго столбца той же строки и прибавить его к принятому слову, получив ближайшее к принятому r = e'j + v' кодовое слово v'.
Таким образом, вместо таблицы n×2n бит для декодирования достаточно использовать таблицу лидеров смежных классов n×2n-k бит.
Пример 6. Снова рассмотрим двоичный линейный (4, 2, 2) код из Примера 3. Положим, что передано было кодовое слово (0110), а принято слово (0010). Тогда синдром равен
s = rHT=(0010)
1 |
||
|
|
|
|
1 |
|
|
1 |
|
|
||
|
||
|
0 |
|
|
||
1 |
||
|
|
|
0 |
|
|
0 |
|
|
|
||
|
||
1 |
|
|
|
||
=(1 0)
Находим в стандартной таблице лидер смежного класса (0100) и получаем декодированное кодовое слово (0010)+(0100)=(0110). Одиночная ошибка в слове исправлена! Это может показаться странным, так как минимальное кодовое расстояние равно 2 и, согласно условию (4.1.2.6), исправление однократных ошибок невозможно. Однако объяснение этому может быть найдено в стандартной таблице (Пример 5). Заметим, что третья строка таблицы содержит два различных двоичных вектора веса 1. Это означает, что только три из возможных четырех одиночных ошибок могут
62
быть исправлены. В Примере 6 дана одна из исправляемых ошибок.
Оказывается, что данный (4, 2, 2) код является простейшим примером линейного кода с неравной защитой от ошибок (linear unequal error protection - LUEP код) [Wv, Van]. Данному LUER коду соответствует разделяющий вектор (3,2), который показывает, что минимальное кодовое расстояние равно трем, если различаются первые биты сообщений и равно двум, если различаются вторые биты сообщений.
В случае систематического кодирования рассмотренная выше процедура находит оценку переданного сообщения на первых k позициях декодированного слова. Это может быть одной из возможных причин применения систематического кодирования.
4.3.3.Хемминговы сферы, области декодирование
истандартная таблица.
Стандартная таблица предоставляет удобный способ объяснения понятий Хемминговой сферы и корректирующей способности линейного кода С, введенной в Разделе 4.1.2.
Из конструкции стандартной таблицы видно, что j-ый столбец из 2k правых столбцов таблицы, обозначаемый Colj, 1< 2k, содержит кодовое слово vj С и множество 2n-к слов, ближайших к нему по Хеммингову расстоянию, т.е.
Colj = {vj +еj |еi
Rowi, 0 < i < 2n-k}
(4.3.3.1)
Каждый столбец (4.3.3.1) представляет собой область декодирования j-ого кодового слова в Хемминговом пространстве. Таким образом, если по ДСК передано кодовое слово vj С и принятое слово r принадлежит столбцу Colj, то оно будет успешно декодировано в переданное слово vj.
63
Граница Хемминга
Множество столбцов Colj и корректирующая способность t кода С связаны между собой через Хеммингову сферу St(vj) следующим образом: двоичный линейный (n,k,d) код С имеет корректирующую способность t, если каждая область декодирования Colj содержит Хеммингову сферу ради-
уса t, т.е. St(yj) Colj.
Учитывая, что каждая область декодирования содержит 2n-k слов, и, используя уравнение (4.4), получаем знаменитую
границу Хемминга
t |
n |
|
|
|
|
|
|
|
i 0 |
i |
|
2n-k
(4.3.3.2)
Граница Хемминга имеет несколько комбинаторных интерпретаций. Вот одна из них:
Число синдромов, 2n-k, должно быть больше или равно
числу исправляемых комбинаций ошибок,
t |
n |
|
|
|
|
|
|
. |
i 0 |
i |
|
Пример 7. Двоичный код (3,1,3) имеет порождающую
матрицу G = (111) и проверочную матрицу
H =
1 |
1 |
0 |
|
|
|
|
. |
|
0 |
1 |
|
1 |
|
Соответственно, стандартная таблица имеет вид:
s |
0 |
1 |
|
|
|
00 |
000 |
111 |
|
|
|
11 |
100 |
011 |
|
|
|
10 |
010 |
101 |
|
|
|
|
64 |
|
01 |
001 |
110 |
|
|
|
Четыре вектора во втором столбце таблицы (т.е. лидеры смежных классов) являются элементами Хемминговой сферы S1(000) показанной на Рисунке 4.3. Этот столбец содержит все векторы длины 3 и веса 1 или меньше. Аналогично, третий столбец (правый) содержит все элементы S1 (111). Для этого кода граница Хемминга выполняется с равенством.
Блоковые коды, удовлетворяющие границе (4.3.3.2) с равенством, называются совершенными кодами. Нетривиальными совершенными кодами являются следующие:
-двоичные (2т - 1, 2т -т - 1, 3) коды Хемминга,
-недвоичные ((qm - 1) / ( q - 1), (qm - 1 ) / ( q - 1) - m - 1, 3)
-коды Хемминга, q > 2 ,
-коды-повторения (n,1,n),
-коды с проверкой на четность (n, n-1,2),
-двоичный (23,12,7) код Голея и
-троичный (11,6,5) код Голея.
Расширенные, т.е. дополненные общей проверкой на четность, коды Хемминга и Голея тоже совершенны.
Для недвоичных кодов граница Хемминга имеет вид:
t |
n |
|
|
|
|
(4.3.3.3) |
|
|
|
(q 1)i qn k |
|
i 0 |
i |
|
|
4.4. Распределение весов и вероятность ошибки.
65
При выборе конкретной схемы кодирования очень важно иметь представление об ее помехоустойчивости. Известны несколько характеристик помехоустойчивости систем с исправлением ошибок. В этом разделе вводятся оценки для линейных кодов и трех базовых моделей каналов: модель ДСК, модель с аддитивным белым гауссовым шумом (АБГШ) и модель канала с общими Релеевскими замираниями.
4.4.1. Распределение весов и вероятность необнаруженной ошибки в ДСК.
Распределение весов W(C)={Ai,0≤i≤n} кода С, исправ-
ляющего ошибки, определено как совокупность п + 1 целых Аi где Аi - количество кодовых слов Хеммингова веса i.
В следующем ниже разделе выводится оценка вероятности необнаруженной ошибки линейного кода в ДСК. Заметим, прежде всего, что вес wt(v) слова v равен Хеммингову расстоянию до нулевого слова, т.е. wt(v) = dH(v,0).
Напомним также, что Хеммингово расстояние между
d |
H |
(v |
,v |
) d |
H |
(v |
v |
,0) wt(v |
v |
) wt(v ) |
|
|
1 |
2 |
|
1 |
2 |
1 |
|
2 |
3 |
||
где из линейности кода следует, что v3 |
C. |
||||||||||
Вероятность необнаруженной ошибки Ри(С) равна вероятности того, что принятое из канала связи слово отличается от переданного, но имеет нулевой синдром, т.е.
s (v e)H T eH T 0 e C
Таким образом, вероятность того, что синдром принятого ненулевого слова равен нулю, есть вероятность того, что вектор ошибок совпадает с одним из ненулевых кодовых слов.
66
В ДСК вектор ошибок веса i возникает с вероятностью, равной вероятности того, что i символов приняты с ошибкой, а остальные n-i приняты правильно. Обозначим вероятность этого события через P(e,i). Тогда
i |
(1 p) |
n i |
P(e,i) p |
|
Для того чтобы возникла необнаруженная ошибка, вектор ошибок должен быть ненулевым кодовым словом. Имеется Ai кодовых слов веса i в кодовом множестве С. Следова-
тельно,
u |
n |
|
|
i |
|
n i |
|
P (C) |
i |
(1 p) |
|
A p |
|
||
|
i d min |
|
|
(4.4.1.1)
Формула (4.4.1.1) дает точное значение Ри(С) в ДСК. К сожалению, для большинства кодов, имеющих практическое значение, распределение весов неизвестно. В таких случаях, можно использовать тот факт, что число кодовых слов веса i меньше (или равно) общего числа слов веса i в двоичном векторном пространстве V2. Следовательно, справедлива следующая верхняя граница:
|
n |
n |
|
|
P (C) |
|
|
pi (1 p)n i |
(4.4.1.2) |
u |
|
|
|
|
|
i d min i |
|
||
Примечание. На самом деле допустима и более сильная оценка:
* |
(C) 2 |
d |
|
1 |
P (C) |
P |
|
m in |
|
||
|
|
|
|
|
|
u |
|
|
|
|
u |
В уравнении еНT = 0 матрица Н имеет ранг p=dmin-1 и, по меньшей мере, ρ неизвестных элементов любого вектора ошибок е определяются однозначно. Следовательно, средняя вероятность того, что произвольный вектор ошибок совпа-
67
дает с некоторым кодовым словом, не превосходит 2-ρ.
Формулы (4.4.1.1) и (4.4.1.2) полезны в системах, использующих помехоустойчивое кодирование только для обнаружения ошибок, как системы связи с обратной связью и автоматическим запросом (ARQ) на повторную передачу сообщения с обнаруженными ошибками. Оценки помехоустойчивости для случая, когда кодирование используется для исправления ошибок, выводятся в следующем ниже разделе.
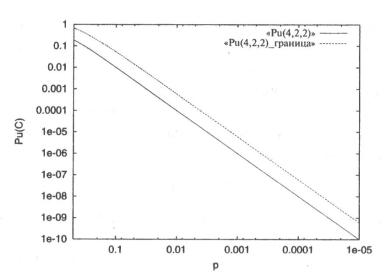
Пример 8. Для двоичного линейного (4,2,2) кода из Примера 4 W(C)=( 1,0,1,2,0). С помощью (1.26) находим
2 |
(1 p) |
2 |
3 |
(1 p) |
P (C) p |
|
2 p |
||
u |
|
|
|
|
На Рисунке 4.5 показана зависимость Ри(С) вместе с правой частью границы (4.4.1.2).
Рис.4.5. Точное значение и верхняя граница вероятности необнаруженной ошибки для двоичного линейного (4,2,2) кода в ДСК.
4.4.2.Границы вероятности ошибки в ДСК, каналах
сАБГШ и с замираниями.
68
Целью этого раздела является введение в базовые модели каналов связи, которые будут рассматриваться в книге, и вывод формул для оценки помехоустойчивости линейных кодов. Первым рассматривается ДСК.
Модель ДСК
Для двоичного линейного кода процедура декодирования с помощью стандартной таблицы состоит в выборе кодового слова, ближайшего к принятому слову. Ошибка декодирования возникает всякий раз, когда принятое слово оказывается вне правильной области декодирования.
Обозначим Li число лидеров смежных классов веса i в стандартной таблице линейного кода С. Вероятность правильного декодирования равна вероятности того, что вектор ошибок совпадает с одним из лидеров смежных классов,
u |
l |
|
|
i |
|
n i |
|
P (C) |
i |
(1 p) |
|
L p |
|
||
|
i 0 |
|
|
(4.4.2.1)
где l это максимальный вес лидера смежного класса е. для совершенных кодов l = t,
L |
n |
i t |
|
|
,0 |
||
i |
|
|
|
|
i |
|
|
и из границы Хемминга (4.22) следует, что
l |
l |
n |
|
|
|
i |
|
|
|
n k |
|
L |
|
|
|
2 |
|
i 0 |
i 0 i |
|
|
||
В общем случае для двоичных кодов выражение (4.4.2.1) дает нижнюю границу РС(С), так как существует хотя бы один лидер смежного класса веса более t.
Вероятность неправильного декодирования Pe(C) или вероятность ошибки декодирования равна вероятности того,
что вектор ошибок принадлежит дополнению множества ис-
69
правляемых ошибок, т.е. Ре(С)=1-РС(С). Из (4.4.2.1) получаем,
e |
l |
|
|
i |
|
n i |
|
P (C) 1 |
i |
(1 p) |
|
L p |
|
||
|
i 0 |
|
|
(4.4.2.2)
Наконец, учитывая обсуждение оценки (4.26), получаем верхнюю границу:
|
|
i |
n |
|
|
n i |
|
|
P |
(C) 1 |
|
|
|
i |
(1 p) |
, |
|
|
p |
|
||||||
e |
|
|
|
|
|
|
|
|
|
|
i 0 |
i |
|
|
|
|
|
которую можно записать и в следующем виде:
(4.4.2.3)
|
n |
n |
|
|
|
|
P (C) |
|
|
|
i |
(1 p) |
n i |
p |
|
|||||
e |
|
|
|
|
|
|
|
i t 1 |
i |
|
|
|
|
(4.4.2.4)
Эти границы удовлетворяются с равенством только для совершенных кодов (когда и граница Хемминга удовлетворяется с равенством).
Пример 9. На Рисунке 4.6 показана зависимость Ре(С) по оценке (4.4.2.4) от переходной вероятности ДСК р для двоичного (совершенного) кода-повторения (3,1,3).
70
