
Министерство науки и высшего образования Российской Федерации Федеральное государственное автономное образовательное учреждение высшего образования
«Национальный исследовательский университет
«Московский институт электронной техники»
Отчет по лабораторной работе №10
«Решение дифференциальных уравнений в частных
производных»
Выполнил студент группы ЭН-22
Проверил преподаватель:
Москва, 2025 г.
Содержание
Цель работы. Задание.
Краткая теория
Описание метода решения.
Программа
Вывод по работе.
Цель работы. Задание.
Цель работы:
Задание:
Решить
уравнение эллиптического типа в
прямоугольной области:

с граничными условиями:


Описание метода решения.
Метод решения:
Используем метод конечных разностей с шаблоном типа “крест” (рис 10.3 лабораторная работа 10)
Дискретизация области:
Шаги
сетки:

Узлы
сетки:

Разностная схема:
Заменяем вторые производные разностными аналогами:

Для
квадратной сетки
 :
:

Итерационный метод Гаусса – Зейделя:
Начальное
приближение:

Итерационный процесс:

Критерий
остановки: max

Программа

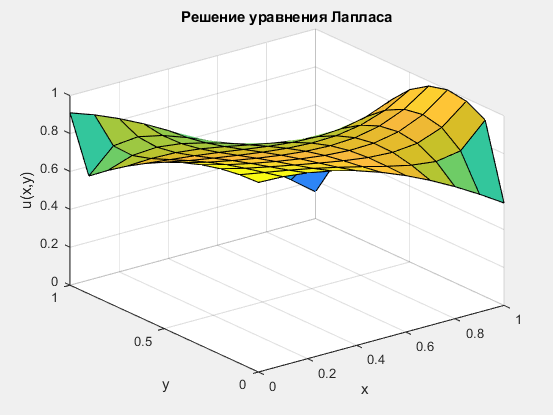
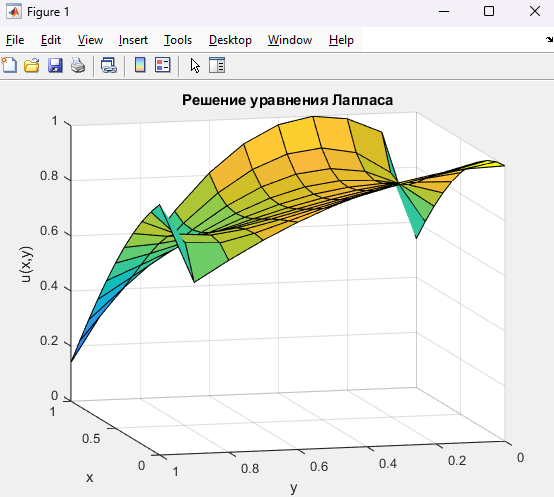
Рис 1,2. Решение уравнения Лапласа.
Вывод
При выполнении данной лабораторной работы были изучены методы решения дифференциальных уравнений в частных производных. И были заключены следующие мысли:
Метод конечных разностей с итерационным решением эффективен для уравнений эллиптического типа.
Схема «крест» обеспечивает устойчивость и простоту реализации.
Результаты соответствуют теоретическим ожиданиям: потенциал плавно изменяется между граничными значениями.
