
Отчет по 4 лабе.Квант.мех
.docxФедеральное государственное автономное образовательное учреждение высшего образования «Национальный исследовательский университет «Московский институт электронной техники»
Отчет по Лабораторной работе №4
Вариант 6
Выполнил:
Студент группы ЭН-22
Цель работы: Исследование движения электрона в потенциальной яме (бесконечно глубокой и конечной глубины) путём расчёта энергетических уровней, волновых функций и вероятностей нахождения электрона в различных областях, а также анализ зависимости числа дискретных уровней от параметров ямы
Задание 1: а = 3.25 А
a, A |
4.25 |
4.25 |
4.25 |
n |
1 |
2 |
3 |
|
3.5377 |
14.1508 |
31.8392 |

Рисунок 1. Три энергетических уровня в бесконечно глубокой яме.
function Task01
% draw energy levels of electron in potential well
% potential well is infinitely deep well
clc; clear;
% Параметры задачи
m = 9.1e-31; % масса электрона (кг)
h = 1.05e-34; % постоянная Планка (Дж*с)
a = 3.25; % ширина потенциального колодца (A, ангстрем)
n = 3; % количество уровней энергии
a_meters = a * 1e-10; % перевод в метры
m1 = 1.6e-19; % Конверсионный коэффициент из Джоулей в эВ
k = zeros(n, 1);
E = zeros(n, 1);
for i = 1:n
k(i) = (i * pi) / a_meters;
E(i) = (((h^(2)) * (k(i)^(2))) / (2 * m)) / m1;
end
figure; % Создаем новую фигуру
% Рисуем потенциальную яму
h2 = line([0 0 a a],[50 0 0 50]);
set(h2,'Color',[0,0,1],'LineWidth',3)
hold on; % Для построения нескольких элементов на одном графике
% Построение уровней энергии
for i = 1:n
line([0, a], [E(i), E(i)], 'Color', 'r', 'LineWidth', 1.5); % Рисуем уровни энергии
text(a / 2, E(i) + 2, ['E_' num2str(i)], 'HorizontalAlignment', 'center'); % Подписываем уровни энергии
end
% Подписи осей и заголовок
xlabel('x (A)', 'FontSize', 12);
ylabel('U, E (eV)', 'FontSize', 12);
title('U(x), E', 'FontSize', 12);
% Установка границ осей
xlim([-1 4]);
ylim([-5 50]);
% Сетка и внешний вид
grid on;
ax = gca; % Получаем текущие оси
ax.GridColor = [0.5 0.5 0.5]; % Темные линии сетки
ax.GridAlpha = 0.5;
text(-0.8, 40, 'U(x)', 'FontSize', 12, 'Color', 'k');
text(1.375, -1.25, 'a', 'FontSize', 12, 'Color', 'k');
text(3.8, -2, 'x', 'FontSize', 12, 'Color', 'k');
hold off;
% Добавление стрелок
annotation('arrow', [0.13 0.905], [0.184 0.184], 'HeadStyle', 'plain', 'LineWidth', 1.5);
annotation('arrow', [0.2845 0.2845], [0.11 0.925], 'HeadStyle', 'plain', 'LineWidth', 1.5);
% Отображение уровней энергии в окне командв
disp('Энергетические уровни (эВ):');
disp(E);
pause;
end
Задание 2.
а=3.25 А

Рисунок 2.Волновые функции 3 первых энергетических уровней электрона в бесконечно глубокой потенциальной яме
function Task02
% draw wave functions of electron in potential well
% potential well is infinitely deep well
clc %clears all from the Command Window
clear %removes all variables from the workspace (memory)
%-------------------------------------------------------------
% PARAMETERS OF TASK
m = 9.1e-31; %mass of electron (kg)
h = 1.05e-34; %Plank's constant (J*s)
a = 3.25; %width of potential well (A, Angstroem)
n_max = 3; % Максимальное значение n для построения
x = linspace(0, a, 70);
% Настройка графика
figure;
xlim([-1 6]);
ylim([-1 1]);
% Рисуем потенциальную яму
h2 = line([0 0 a a],[10 -10 -10 10]);
set(h2,'Color',[0,0,1],'LineWidth',3)
hold on;
colors = ['r', 'g', 'm']; % Цвета для разных n
% Вычисление и построение графиков
for n = 1:n_max
k_n = pi * n / a;
psi_n = sqrt(2/a) * sin(k_n * x);
plot(x, psi_n, 'Color', colors(n), 'LineWidth', 1.5, 'DisplayName', sprintf('n = %d', n));
end
% Оформление
title('\Psi(x)');
xlabel('x (A)');
ylabel('\Psi (A^{-1/2})');
grid on;
hold off;
% Добавление стрелок
annotation('arrow', [0.13 0.905], [0.52 0.52], 'HeadStyle', 'plain', 'LineWidth', 1.5);
annotation('arrow', [0.285 0.285], [0.11 0.925], 'HeadStyle', 'plain', 'LineWidth', 1.5);
% Добавление подписей на графике (Ψ₁, Ψ₂, Ψ₃)
text(1.32, 0.92, '\Psi_1', 'Color', 'k', 'FontSize', 12);
text(2, -0.92, '\Psi_2', 'Color', 'k', 'FontSize', 12);
text(1.35, -0.92, '\Psi_3', 'Color', 'k', 'FontSize', 12);
text(2.85, -0.05, 'a', 'Color', 'k', 'FontSize', 12);
text(3.75, -0.05, 'x', 'Color', 'k', 'FontSize', 12);
text(-0.5, 0.92, '\Psi(x)', 'Color', 'k', 'FontSize', 12);
pause
end
Задание 3.
а=3.25 А
|
P(0<x<a/3) |
P(a/3<x<2a/3) |
P(2a/3<x<a) |
|
|
0.1940 |
0.4007 |
0.333 |
0.9969 |
|
0.6074 |
0.1940 |
0.333 |
0.9969 |
|
0.1955 |
0.4022 |
0.333 |
1 |
function Task03
clc
clear
%-------------------------------------------------------------
% PARAMETERS OF TASK
m = 9.1e-31; %mass of electron (kg)
h = 1.05e-34; %Plank's constant (J*s)
a = 3.25; %width of potential well (A, Angstroem)
n_max = 3;
% Интервалы
x1 = 0:0.01:a/3;
x2 = a/3:0.01:2*a/3;
x3 = 2*a/3:0.01:a;
for n = 1:n_max
% Функции
y1 = (sqrt(2/a)*sin(n*pi*x1/a)).^2;
y2 = (sqrt(2/a)*sin(n*pi*x2/a)).^2;
y3 = (sqrt(2/a)*sin(n*pi*x3/a)).^2;
% Интегрируем каждый интервал
I1 = trapz(x1, y1);
I2 = trapz(x2, y2);
I3 = trapz(x3, y3);
% SСуммируем вероятности
sum_n = I1 + I2 + I3;
% Выводим результаты
fprintf('For n = %d:\n', n);
fprintf(' Probability in region 1: %.4f\n', I1);
fprintf(' Probability in region 2: %.4f\n', I2);
fprintf(' Probability in region 3: %.4f\n', I3);
fprintf(' Sum for n=%d: %.4f\n\n', n, sum_n);
end
end
Задание 4.
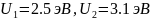

|
|
|
, эВ |
, эВ |
, эВ |
8.3 |
2.5 |
3.1 |
0.3273 |
1.2655 |
2.4999 |
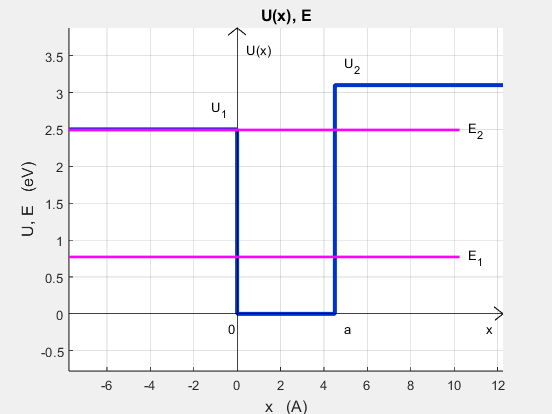
|
, эВ |
, эВ |
, эВ |
, эВ |
4.2 |
2.5 |
3.1 |
0.7710 |
2.4933 |

|
, эВ |
, эВ |
, эВ |
0.6 |
2.5 |
3.1 |
2.4976 |
Задание 5.


|
P(-∞<x<0) |
P(0<x<a) |
P(a<x<+∞) |
|
|
0.0181 |
0.9689 |
0.0129 |
1 |
|
0.0922 |
0.8482 |
0.0595 |
1 |
|
0.0661 |
0.6338 |
0.3002 |
1 |
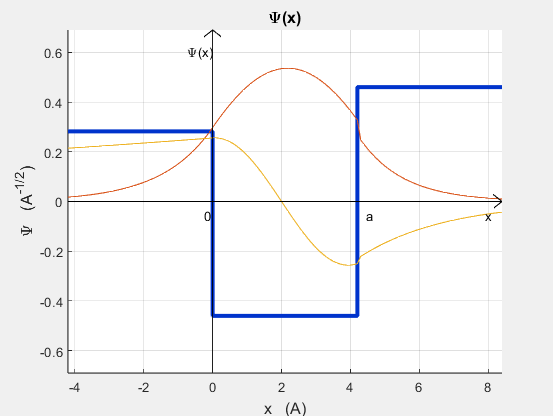

|
P(-∞<x<0) |
P(0<x<a) |
P(a<x<+∞) |
|
|
0.0656 |
0.8888 |
0.0456 |
1 |
|
0.7781 |
0.1560 |
0.0659 |
1 |


|
P(-∞<x<0) |
P(0<x<a) |
P(a<x<+∞) |
|
|
0.9266 |
0.0263 |
0.0472 |
1 |

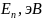

 ,
,
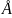
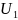 ,
эВ
,
эВ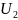 ,
эВ
,
эВ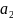 ,
,
 ,
,