
3 сем / лаб4
.docxМинобрнауки России
Санкт-петербургский государственный
Электротехнический университет
«ЛЭТИ» им. В.И. Ульянова (Ленина)
Кафедра вычислительной техники
Отчёт
Лабораторная работа №4
По дисциплине «АиСД»
Тема: графы
Студент гр. 3316 |
|
Руденский И.М. |
Преподаватель |
|
Манирагена Валенс |
Санкт-Петербург
2024
Формулировка задания
Получение минимального вершинного покрытия для двудольного неориентированного графа.


Обоснование выбора способа представления и анализ сложности алгоритма
Структура_данных Граф представлен в виде списка смежности с использованием std::unordered_map, где ключ — вершина, а значение — список её соседей. Это позволило обеспечить компактное хранение и быстрый доступ к вершинам и их связям. Преимущества выбранного способа:
Список смежности занимает O(V+E) памяти, где V — количество вершин, E — количество рёбер. Это лучше, чем O(V^2) для матрицы смежности при разреженных графах.
Мы можем легко добавлять новые рёбра и получать доступ к соседям вершины за O(1) времени.
Описание алгоритма
Алгоритм использует жадный подход для приближённого поиска минимального вершинного покрытия:
Инициализация: создаётся список для хранения вершинного покрытия и массив для отслеживания, какие рёбра уже покрыты.
Выбор вершины: на каждом шаге выбирается вершина с максимальной степенью (количеством непокрытых рёбер).
Добавление в покрытие: выбранная вершина добавляется в множество покрытия, и все её инцидентные рёбра помечаются как покрытые. Вершины, инцидентные данной, удаляются из списка edges.
Повторение: шаги повторяются до тех пор, пока все рёбра графа не будут покрыты.
Результат: возвращается множество вершин, которые составляют приближённое минимальное вершинное покрытие.
Оценка временной сложности
Инициализация:
Создание массива для отслеживания покрытых рёбер и списка вершин занимает O(V), где V — количество вершин.
Поиск вершины с максимальной степенью:
Для каждой вершины необходимо подсчитать количество инцидентных непокрытых рёбер. Это занимает O(V+E) на каждой итерации.
Добавление в покрытие и пометка рёбер:
Покрытие рёбер инцидентных вершине требует O(степень вершины) что суммарно занимает O(E) за все шаги.
Итерации:
Максимальное количество итераций равно V, так как в худшем случае каждая вершина добавляется в покрытие.
Суммарная временная сложность:
O(V⋅(V+E))=O(V^2+V⋅E)
В разреженных графах (E≈V) сложность упрощается до O(V^2), а в плотных графах (E≈ V^2) — до O(V^3).
Результаты проверки работы алгоритма
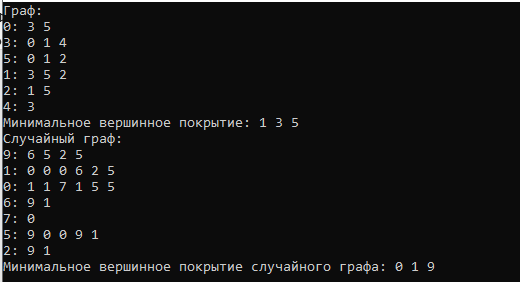
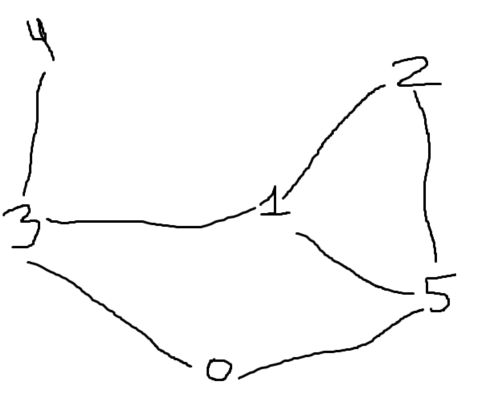
Пример работы алгоритма для заготовленного графа:
Инициализация: Все рёбра: (0,3),(0,5),(1,3),(1,5),(1,2),(2,5),(3,4)
Первая итерация:
Степени вершин: {0:2,1:3,2:2,3:3,4:1,5:3}.
Вершина с максимальной степенью: 1.
Добавляем 1 в покрытие: C={1}.
Удаляем рёбра, связанные с 1: остаются (0,3),(0,5),(3,4).
Вторая итерация:
Степени вершин: {0:2,3:2,4:1,5:1}.
Вершина с максимальной степенью: 3.
Добавляем 3 в покрытие: C={1,3}.
Удаляем рёбра, связанные с 3: остаётся (0,5).
Третья итерация:
Степени вершин: {0:1,5:1}.
Вершина с максимальной степенью: 5.
Добавляем 5 в покрытие: C={1,3,5}.
Все рёбра покрыты.
Вывод
В результате выполнения работы был реализован алгоритм поиска минимального вершинного покрытия для неориентированного графа. Была выбрана подходящая структура данных, разработана объектная модель графа, а также реализован удобный интерфейс для ввода данных и тестирования. Все необходимые навыки по работе с графами были освоены.
Список использованных источников
Ахо А., Хопкрофт Д., Ульман Дж. Структуры данных и алгоритмы. — М.: Мир, 1986.
Роберт Седжвик. Алгоритмы на C++. Фундаментальные алгоритмы. — М.: Вильямс, 2003.
Дональд Кнут. Искусство программирования. Том 3: Сортировка и поиск. — М.: Вильямс, 2002.
Джосеф А. Р. О'Рурк. Основы алгоритмов и структур данных. — СПб.: Питер, 2010.
Cormen T., Leiserson C., Rivest R., Stein C. Introduction to Algorithms. — MIT Press, 2009.
Документация по C++: https://en.cppreference.com
Документация по STL: https://cplusplus.com/reference/
Приложение
#include <iostream>
#include <vector>
#include <set>
#include <algorithm>
#include <sstream>
#include <unordered_map>
#include <queue>
#include <locale>
class Graph {
private:
std::unordered_map<int, std::vector<int>> adjacencyList;
public:
// Конструктор по умолчанию
Graph() = default;
// Метод для добавления ребра
void addEdge(int u, int v) {
adjacencyList[u].push_back(v);
adjacencyList[v].push_back(u);
}
// Метод для вывода графа
void printGraph() const {
for (const auto& [vertex, neighbors] : adjacencyList) {
std::cout << vertex << ": ";
for (int neighbor : neighbors) {
std::cout << neighbor << " ";
}
std::cout << std::endl;
}
}
// Метод для нахождения минимального вершинного покрытия
std::set<int> findMinimumVertexCover() {
std::set<int> vertexCover;
std::set<std::pair<int, int>> edges;
// Собрать все рёбра
for (const auto& [u, neighbors] : adjacencyList) {
for (int v : neighbors) {
if (u < v) {
edges.emplace(u, v);
}
}
}
while (!edges.empty()) {
// Найти вершину с максимальной степенью
std::unordered_map<int, int> degree;
for (const auto& [u, v] : edges) {
degree[u]++;
degree[v]++;
}
int maxDegreeVertex = -1;
int maxDegree = -1;
for (const auto& [vertex, deg] : degree) {
if (deg > maxDegree) {
maxDegree = deg;
maxDegreeVertex = vertex;
}
}
// Добавить вершину с максимальной степенью в покрытие
vertexCover.insert(maxDegreeVertex);
// Удалить все рёбра, инцидентные этой вершине
for (auto it = edges.begin(); it != edges.end(); ) {
if (it->first == maxDegreeVertex || it->second == maxDegreeVertex) {
it = edges.erase(it);
}
else {
++it;
}
}
}
return vertexCover;
}
// Метод для генерации случайного графа
static Graph generateRandomGraph(int numVertices, int numEdges) {
Graph graph;
srand(time(nullptr));
for (int i = 0; i < numEdges; ++i) {
int u = rand() % numVertices;
int v = rand() % numVertices;
if (u != v) {
graph.addEdge(u, v);
}
}
return graph;
}
};
int main() {
setlocale(LC_ALL, "russian");
Graph graph;
// Пример ввода заранее заготовленного графа
graph.addEdge(0, 3);
graph.addEdge(0, 5);
graph.addEdge(1, 3);
graph.addEdge(1, 5);
graph.addEdge(1, 2);
graph.addEdge(2, 5);
graph.addEdge(3, 4);
std::cout << "Граф:" << std::endl;
graph.printGraph();
// Нахождение минимального вершинного покрытия
std::set<int> vertexCover = graph.findMinimumVertexCover();
std::cout << "Минимальное вершинное покрытие: ";
for (int vertex : vertexCover) {
std::cout << vertex << " ";
}
std::cout << std::endl;
// Генерация случайного графа для тестирования
Graph randomGraph = Graph::generateRandomGraph(10, 15);
std::cout << "Случайный граф:" << std::endl;
randomGraph.printGraph();
std::set<int> randomVertexCover = randomGraph.findMinimumVertexCover();
std::cout << "Минимальное вершинное покрытие случайного графа: ";
for (int vertex : randomVertexCover) {
std::cout << vertex << " ";
}
std::cout << std::endl;
return 0;
}
