Вопрос 2: Прохождение случайных сигналов через нелинейные цепи.

Решение задачи преобразования случайных сигналов линейными радиотехническими цепями осуществлялось спектральным методом. При этом, определялись характеристики  ,  ,   при известных   и комплексном коэффициенте передачи цепи  . Что касается функции распределения   или плотности вероятности   значений выходного процесса, то задача их определения является достаточно сложной и поддается решению лишь в отдельных частных случаях.

При решении задачи преобразования случайного процесса нелинейными цепями, наоборот, плотность вероятности   определяется сравнительно просто, а определение   и   сопряжено со значительными трудностями. Поэтому, постановка задачи преобразования СП нелинейными цепями отличается от постановки задачи преобразования СП линейными инерционными цепями.

Напомним, что основной характеристикой нелинейного безынерционного элемента является вольт – амперная характеристика

, (6.28), где   – входной сигнал,  – выходной сигнал нелинейного элемента.

Отметим, что входной и выходной сигналы связаны детерминированной функциональной зависимостью  .

Так как в рассмотренном случае входной и выходной сигналы являются случайными процессами, т.е.

,  , то выражение (6.28) можно записать так . (6.29)

Сформулируем теперь задачу. На вход безынерционного нелинейного элемента, описываемого характеристикой (6.29) поступает стационарный случайный процесс   с известной плотностью вероятности   (рис. 6.9). Необходимо определить плотность распределения вероятности   выходного процесса  . Задачу будем решать при следующих предположениях:

– входной процесс   является стационарным эргодическим процессом;

– существует и известна функция

, (6.30) обратная функции  .

Изобразим на рис. 6.10 а) зависимость   и реализации входного и выходного случайных процессов.

Поскольку процесс   подвергается неслучайному функциональному преобразованию   этому же преобразованию подвергается и плотность вероятности  . На рис. 6.10б показана характеристика   и кривые плотности вероятности   и   входного и выходного случайных процессов.

Установим соответствие между   и  . Выберем некоторое значение   входного процесса. Этому значению однозначно соответствует значение   выходного процесса. Придадим значению   элементарное приращение  . Этому приращению будет соответствовать элементарное приращение   выходного процесса. Так как зависимость   однозначна, то вероятность того, что значение случайной величину   будет находиться в пределах  , должна быть равна вероятности того, что случайная величина   будет находится в пределах  , т.е.

. (6.31)

Но, с другой стороны , .

Тогда (6.31) можно представить следующим образом , (6.32) откуда следует

. (6.33)

Производная в (6.33) вычисляется по абсолютной величине (по модулю) в силу того, что функция   может быть отрицательной, а плотность вероятности   всегда положительна.

Так как по условию задачи известна функция обратная  , т.е.  , то (6.33) можно записать так

. (6.34)

Выражение (6.34) является основным результатом решения задачи нелинейного преобразования.

Если функция   неоднозначна (имеет несколько ветвей (рис. 6.10 в)), то (6.34) принимает вид

. (6.35)

Перейдем к определению вероятностных характеристик выходного процесса. Математическое ожидание при известном   определяется следующим образом .

Но с другой стороны, учитывая (6.32), а также  , получим . (6.36)

Аналогично, для дисперсии . (6.37)

Расчеты по этой формуле достаточно просты, если   допускает степенную аппроксимацию.

Выражение (6.34) позволяет найти   при конкретном виде зависимости  . Так, пусть на вход нелинейного элемента с характеристикой  ,   поступает случайный сигнал с нормальной одномерной плотностью вероятности (рис. 6.11)

. (6.38)

Найдем функцию, обратную функции  .

Модуль первой производной

. Далее отметим, что функция   двузначна (имеет две ветви) и сигнал   при любом   принимает неотрицательные значения.

С учетом отмеченных обстоятельств, воспользовавшись (6.35) запишем:

Но для нормального закона (6.38)

  ,

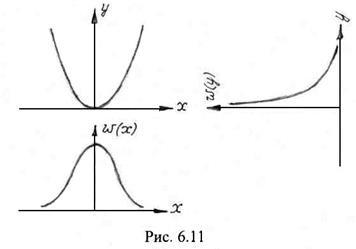
Тогда окончательно получим на рис. 6.11 изображена кривая плотности вероятности  .

БИЛЕТ № 19

Вопрос 1: Спектральное представление случайных сигналов. Теорема Винера-Хинчина. Для описания случайных сигналов, описываемых случайными функциями, может быть применен подход, аналогичный представлению детерминированных сигналов совокупностью элементарных базисных сигналов.

Действительно, пусть случайная функция  имеет математическое ожидание и соответствующую центрированную случайную функцию : . (2.128)

Центрированную случайную функцию  можно выразить в виде суммы ортогональных составляющих, каждая из которых состоит из произведения неслучайной базисной функции и коэффициента разложения , являющегося случайной величиной: . (2.129)

Неслучайные базовые функции называют координатными функциями. Коэффициенты разложения  в общем статистически зависимы и эта зависимость может быть задана матрицей коэффициентов корреляции . Для конкретной реализации коэффициенты разложения могут быть определены из выражения: , (2.130)

где  - интервал существования случайной функции . Предположив, что неслучайная функция  ограничена, то есть , (2.131) ее также можно представить в виде разложения по ортогональным функциям  : ; (2.132) . (2.133)

Тогда выражение (2.128) с учетом (2.129) и (2.133) преобразуется к виду: , (2.134)

который позволяет существенно упростить линейные преобразования случайного сигнала.

Для определения требований к координатным функциям полезно рассмотреть корреляционную функцию центрированной случайной функции  . По определению (2.135)

Так как в общем случае то

. (2.136)

Если предположить, что коэффициенты  некоррелированы, то есть то выражение (2.136) существенно упрощается: . (2.137)

В частном случае, при  корреляционная функция обращается в дисперсию случайной функции : . (2.138)

Поэтому в качестве координатных функций  целесообразно выбирать такие функции, которые обеспечили бы некоррелированность коэффициентов разложения . Разложение (2.129), использующее такие функции, называют каноническим разложением. В этом случае центрированная случайная функция будет характеризоваться совокупностью дисперсий коэффициентов разложения, которую можно рассматривать как обобщенный спектр случайной функции. Этот спектр при каноническом разложении (2.129) является дискретным (линейчатым) и может содержать как конечное, так и бесконечное число линий.

Основной трудностью при использовании канонического разложения является определение координатных функций, однако для стационарных случайных функций эта операция легко выполнима.

Теорема Винера-Хинчина.

Энергетический спектр и автокорреляционная функция случайного процесса являются неслучайными функциями, связанными между собой. Установим эту связь. Рассмотрим реализацию   случайного процесса длительностью   и ее копию  , сдвинутую на интервал времени  . Известно, что энергетический спектр и автокорреляционная функция детерминированного сигнала связаны между собой парой преобразований Фурье. Тогда с учетом выше приведенного предположения о том, что реализация   и ее копия   нам известны, можно записать .

Разделим обе части этого равенства на  : , (5.62) и устремим  .

Тогда в соответствии с (5.51) левая часть равенства (5.62) представляет собой автокорреляционную функцию  . Учитывая (5.59) равенство (5.62) можно представить следующим образом

. (5.63)

Но это есть обратное преобразование Фурье, связывающее АКФ случайного процесса с его энергетическим спектром. Очевидно, если существует обратное преобразование, значит, существует и прямое преобразование Фурье , (5.64) связывающее энергетический спектр с АКФ.

Таким образом, АКФ случайного процесса и его энергетический спектр связаны между собой парой преобразований Фурье. Впервые эта связь была установлена советским математиком А. Хинчиным и независимо от него американским ученым Н. Винером. Поэтому соотношения (5.63) и (5.64) носят название теоремы Винера–Хинчина.

Так как автокорреляционная функция   и энергетический спектр   являются вещественными четными функциями, можно отказаться от комплексной формы записи преобразования Фурье и перейти к другой форме , (5.65) . (5.66)

Из этих выражений следует , (5.67) . (5.68)

Но  , откуда , что совпадает с (5.60).

В случае, когда энергетический спектр описывается функцией циклической частоты (5.61), выражения (5.65) – (5.68) приобретают вид

, (5.69) . (5.70)

, (5.71) . (5.72)