Министерство науки и высшего образования Российской Федерации
Федеральное государственное бюджетное образовательное учреждение
высшего образования
«Ярославский государственный технический университет»
Кафедра «Охрана труда и природы»
Реферат принят
с оценкой ______________
Руководитель,
_________В.В.Макарьин
«____»___________2025
Программная реализация методов решения нелинейных уравнений
Контрольная работа по дисциплине
«Моделирование энерго- и ресурсосберегающих процессов в химической технологии, нефтехимии и биотехнологии»
ЯГТУ 18.03.02 – 016 Р
-
Контрольную работу выполнил
студент группы ЗОС-41
___________
«____»___________2025
2025
Р еферат
17 стр., 9 рис., 3 ист..
Уравнение, отрезок, теорема, замечание.
Объектом исследования являются нелинейные уравнения.
Цель работы – изучить и описать программную реализацию методов решения нелинейных уравнений.
В процессе работы описаны методов решения нелинейных уравнений.
Содержание
Реферат 2
Введение 4
1 Численные методы решения нелинейных уравнений 5
1.1 Постановка задачи и основные этапы нахождения решения 5
1.2 Метод деления отрезка пополам 6
1.3 Метод простых итераций 7
1.4 Метод касательных 11
1.5 Метод секущих 12
1.6 Метод ложного положения 14
Заключение 16
Список использованных источников 17
Введение 4
1 Численные методы решения нелинейных уравнений 5
1.1 Постановка задачи и основные этапы нахождения решения 5
1.2 Метод деления отрезка пополам 6
1.3 Метод простых итераций 7
1.4 Метод касательных 11
1.5 Метод секущих 12
1.6 Метод ложного положения 14
Заключение 16
Список использованных источников 17
Введение
Во многих конкретных случаях найти решение задачи в явном виде не представляется возможным, так как оно не выражается через элементарные функции. Такие задачи можно решить лишь приближенно. Под вычислительными (численными) методами подразумеваются приближенные процедуры, позволяющие получать решение в виде конкретных числовых значений. Для решения одной и той же задачи могут быть использованы различные вычислительные методы, поэтому нужно уметь оценивать качество различных методов и эффективность их применения для данной задачи.
1 Численные методы решения нелинейных уравнений
Постановка задачи и основные этапы нахождения решения
Пусть дана некоторая функция f(x) и требуется найти все или некоторые значения x, для которых f(x) = 0.
Значение x*, при котором f(x*) = 0, называется корнем (или решением) уравнения.
Относительно функции f(x) часто предполагается, что f(x) дважды непрерывно дифференцируема в окрестности корня.
Корень x* уравнения называется простым, если первая производная функции f(x) в точке x* не равна нулю, то есть f '(x*) =/= 0. Если же f '(x*) =/= 0, то корень x называется кратным корнем.
Геометрически корень уравнения есть точка пересечения графика функции y = f(x) с осью абсцисс. На рис. 1 изображен график функции y = f(x), имеющей четыре корня: два простых (x*1 и x*3) и два кратных (x*2 и x*4).
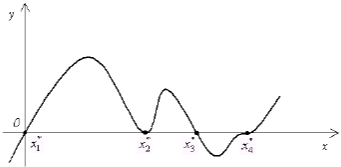
Рисунок 1 – График функции y = f(x)
Большинство методов решения уравнения ориентировано на отыскание простых корней уравнения.
В процессе приближенного нахождения корней уравнения обычно выделяют два этапа: локализация (или отделение) корня и уточнение корня.
1 этап. Локализация корня заключается в определении отрезка [a,b], содержащего один и только один корень. Не существует универсального алгоритма локализации корня. В некоторых случаях отрезок локализации может быть найден из физических соображений. Иногда удобно бывает локализовать корень с помощью построения графика или таблицы значений функции y = f(x). На наличие корня на отрезке [a, b] указывает различие знаков функции на концах отрезка. Основанием для этого служит следующая теорема математического анализа.
Теорема 1. Если функция f непрерывна на отрезке [a, b] и принимает на его концах значения разных знаков, так, что f(a)f(b) < 0, то отрезок [a, b] содержит, по крайней мере, один корень уравнения f(x) = 0.
Однако корень четной кратности таким образом локализовать нельзя, так как в окрестности такого корня функция f(x) имеет постоянный знак.
этап. На этапе уточнения корня вычисляют приближенное значение корня с заданной точностью ε > 0 Приближенное значение корня уточняют с помощью различных итерационных методов. Суть этих методов состоит в последовательном вычислении значений x0, x1, …, xn, …, которые являются приближениями к корню x*.