8

Кафедра КФН, Электромагнитные поля и волны

Лабораторная работа №5

Образование и пространственное распределение стоячих волн в передающих линиях.

1. Общие положения

Источники сигналов и приёмные нагрузки соединяются линиями связи, линиями передачи. В зависимости от частоты сигнала и собственных свойств эти линии по разному передают выполняют функцию передачи энергии. Известно, что в случае, когда линией передачи можно пренебречь (близкое расположение источника сигнала (генератора) и приёмника и по вносимым потерям и по волновым свойствам, максимальная мощность от генератора передаётся в нагрузку только при выполнение условия равенства величин сопротивлений генератора R_Г и нагрузки R_Н. Линии передачи также характеризуются сопротивлением, но физически, это сопротивление другой природы и определяется геометрическими и диэлектрическими свойствами передающей линии и её среды. Передающими линиями могут быть микрополоски, кабели, волноводы, двухпроводные линии, витые пары, копланарные и щелевые микрополоски. Эквивалентная электрическая схема таких линий передач представляет собой последовательность элементарных ячеек (рис.1), состоящих из последовательно соединенных сопротивления R и индуктивности L и параллельно соединенных ёмкости С и проводимости g.

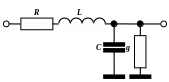
Рис.1. Элементарная ячейка эквивалентной электрической схемы линии передачи

В настоящей работе будут использоваться коаксиальные кабели. Под коаксиальным кабелем (коаксиальной линией передачи) понимается система, образованная двумя металлическими коаксиальными цилиндрами радиусов R₁ и R₂, служащая для проведения электромагнитной волны, распространяющейся в кольцеобразном пространстве, заключенном между цилиндрами.

Линии передач характеризуются двумя основными параметрами: волновым сопротивлением _В и постоянной распространения .

Волновое сопротивление – это электрическая характеристика линии передачи (кабеля, разъёмов, и других элементов линии), описывающая ее способность передавать переменный ток. Условием эффективной передачи электрических сигналов на расстояние является правило согласования волновых сопротивлений: все элементы линии связи должны иметь одинаковое волновое сопротивление. При его нарушении происходит отражение сигнала от места контакта несогласованных элементов, при этом в следующий элемент попадает только часть энергии волнового сигнала, что приводит к постепенному затуханию волны в линии. Омическое сопротивление линии также вызывает затухание сигнала, поэтому его стремятся делать как можно меньше.

Волновое сопротивление линии равно корню квадратному отношения распределенной вдоль линии индуктивности (погонной индуктивности) к распределенной вдоль этой же линии емкости (погонной емкости). Физически волновое сопротивление линии показывает, какое эквивалентное сопротивление линия оказывает генератору. Хотя волновое сопротивление рассчитывается исходя из реактивных сопротивлений, оно имеет активный характер. Физически это соответствует тому, что линия потребляет энергию от генератора.

,

(1)

где L - погонная индуктивность линии [нГн/м], а С - погонная ёмкость линии [пФ/м].

Так как размерность величины _В - [Ом], то она является сопротивлением.

Волновое сопротивление _В в некоторой степени характеризует скорость распространения сигнала v, так как

,

(2)

Постоянная распространения определяется по следующей формуле.

=+j,

(3)

где  характеризует степень затухания волны вдоль линии, а  - изменение фазы волны вдоль линии.

При наличии линии передачи с волновым сопротивлением _В условие передачи максимальной мощности требует равенства всех сопротивлений, то есть R_Г=R_Н=_В. Это есть условие согласования, то есть режима работы линии, при котором равенство сопротивлений обеспечивает «однородность» электрической цепи в смысле равенства сопротивлений, что обеспечивает режим бегущей волны напряжения. При отличии сопротивлений возникает неоднородность, от которой происходит отражение волн, и часть энергии возвращается обратно к генератору. Условие равенства сопротивлений (а в общем случае – импедансов – полных комплексных сопротивлений) есть необходимое условие для максимальной передачи энергии в режиме бегущей волны. В комплексном виде е волновое сопротивление z_В и постоянная распространения  могут быть представлены в следующем виде длинная линия.

,	(4)
,	(5)

Решение телеграфных уравнений для линии передачи позволяет выяснить каков закон распределения токов и напряжений в линии в зависимости от волнового сопротивления и постоянной распространения. Ниже приведены эти выражения.

,	(6)
,	(6)

Таким образом, в «длинной» линии волна имеет пространственную зависимость. Какую линию следует считать «длинной»? На этот вопрос можно ответить только зная длину волны (или частоту) передаваемого сигнала или переменного напряжения. Определённая скорость волны и распределённые параметры линии передачи порождают особые свойства цепей передачи только в том случае, когда геометрические размеры элементов цепи становятся соизмеримыми с длиной волны переменного напряжения. Например, при частоте 1 кГц длина волны в свободном пространстве равна 30 км (=c/f), то есть для таких частот 30 км - это «длинная» линия с распределёнными параметрами. А при частоте 10 ГГц (обычная частота современных систем) длина волны равна 3 см (для вакуума, то есть при =1). Микрополоски и кабели - это среда, у которой относительная диэлектрическая проницаемость  может существенно превышать 1 и составлять от 2 до 100. Длина волны в диэлектрической среде существенно зависит от ее относительной диэлектрической проницаемости.

,

(7)

где .

В результате эффект «длинной» линии может проявиться таким образом, что отрезки уже миллиметровой длины станут «длинными» линиями.

Распределение волн вдоль линий передач описывается теперь следующими уравнениями для тока и напряжения.

,

(8)

где l – длина линии, x – текущая координата.

Полное комплексное сопротивление нагрузки может быть:

• чисто активным, равным или не равным волновому сопротивлению,

• смешанным,

• чисто ёмкостным,

• чисто индуктивным.

Для каждого случая линия будет работать в разных режимах передачи энергии. Кроме того, возможны случаи:

• короткого замыкания (КЗ), то есть Z_Н=R_Н=0,

• холостого хода (ХХ), то есть Z=R→∞.

Наиболее важными являются режимы согласования R_Н=Z_В и рассогласования R_Н≠Z_Н. В последнем случае падающая волна от генератора порождает отражённую волну от нагрузки и величина амплитуды отраженной волны зависит от разности величин сопротивлений и характеризуется коэффициентом отражения, значение которого при активном сопротивлении нагрузки R_Н составляет

.

(9)

Закон распределения волны в пространстве описывается следующими уравнениями.

,

(10)

При равенстве сопротивления нагрузки и волнового сопротивления R_Н=_B =0, и мы имеем режим бегущей волны. А при неравенстве сопротивления нагрузки и волнового сопротивления R_Н≠_B получаем режим смешанных волн, когда происходит суперпозиция отражённой и падающей волн. Это порождает стоячую волну, описываемую следующим выражением.

.

(11)

То есть распространяющаяся вдоль оси X волна имеет косинусоидальный (синусоидальный) вид, амплитуда которой в каждой точке колеблется с частотой ω. Модуль комплексного выражения U(x) можно записать следующим образом.

.

(12)

Дифференцируя это выражение для нахождения точек экстремума (минимума и максимума) стоячей волны, получим следующее выражение.

.

(13)

Выражение (13) показывает, что в конце линии l (на расстоянии /4) устанавливаются минимумы и максимумы напряжения. Отношение этих величин называется коэффициентом стоячей волны по напряжению – КСВН=k=U_max/U_min.

КСВН связан с коэффициентом отражения следующим соотношением.

.

(14)

Таким образом, измерив КСВН, можно определять отражение, величину сопротивления нагрузки и степень рассогласования, а, следовательно, коэффициент полезного действия при передаче энергии.

КСВН можно измерить и по значениям мощности в минимуме и максимуме, зная, что напряжение и мощность связаны квадратичной зависимостью.
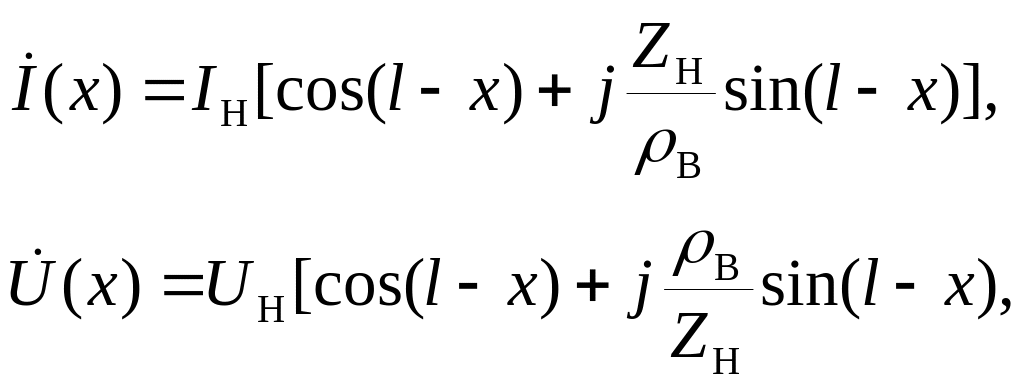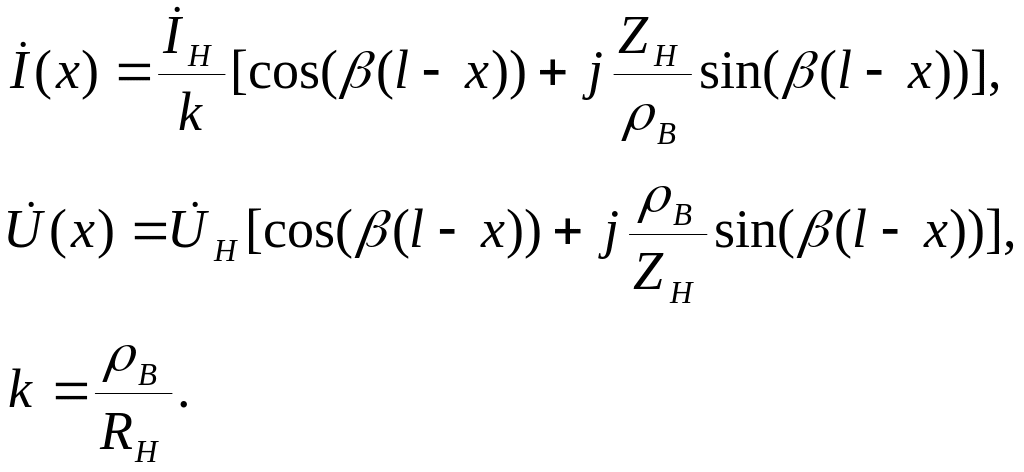