Электромагнитные поля и волны

МОСКОВСКИЙ ОРДЕНА ТРУДОВОГО КРАСНОГО ЗНАМЕНИ

ИНСТИТУТ ЭЛЕКТРОННОЙ ТЕХНИКИ

УТВЕРЖДАЮ

Зав. кафедрой КФН,

профессор

______________А.А. Горбацевич

«___» ________ 2013 г.

ЛАБОРАТОРНАЯ РАБОТА № 2

по курсу «Электромагнитные поля и волны»

Распространение импульсного сигнала в длинных линиях

Авторы работы:

доцент В.И.Корнеев,

ст. преподаватель С.Б. Бурзин,

вед.инженер Б.Г.Налбандов

Москва 2013

Распространение импульсного сигнала в длинных линиях

1. Цель работы

Целью работы является ознакомление с распространением электромагнитных волн в длинной линии, в частности, в коаксиальном кабеле, нахождение коэффициентов отражения и затухания, определение скорости прохождения импульса напряжения по кабелю.

2. Общие сведения

Источники сигналов и приёмные нагрузки соединяются линиями передачи. Линии передачи (длинные линии) – это многопроводные системы, состоящие из параллельных проводников, вдоль которых могут распространяться электромагнитные волны. Поперечные размеры таких систем малы по сравнению с продольными размерами и с длиной волны. В зависимости от частоты передаваемого сигнала и собственных свойств эти линии по-разному выполняют функцию передачи энергии. В случае, когда линией передачи можно пренебречь (близкое расположение источника сигнала и приёмника) и по вносимым потерям и по волновым свойствам, максимальная мощность от генератора передаётся в нагрузку только при выполнение условия равенства выходного сопротивления генератора R_Г и входного сопротивления нагрузки R_Н.

Различают экранированные линии передач и открытые. Передающими линиями могут быть волноводы, микрополоски, копланарные и щелевые микрополоски, коаксиальные кабели, двухпроводные линии, витые пары. Эквивалентную электрическую схему таких линий передачи можно представить в виде последовательности соединенных друг с другом элементарных ячеек (рис.1).

.

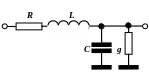
Рис.1. Элементарная ячейка эквивалентной электрической схемы линии передачи

В настоящей работе в качестве длинной линии будет использоваться коаксиальный кабель (в дальнейшем – кабель). Под таким кабелем (или коаксиальной линией передачи) понимается система, образованная двумя металлическими коаксиальными цилиндрами радиусов R₁ и R₂, служащая для проведения электромагнитной волны, распространяющейся в кольцеобразном пространстве, заключенном между цилиндрами и заполненном диэлектриком.

Линии передач характеризуются двумя основными параметрами: постоянной распространения  и волновым сопротивлением _В.

Волновое сопротивление – это электрическая характеристика линии передачи (кабеля, разъёмов, и других элементов линии), описывающая ее способность передавать переменный ток. Условием эффективной передачи электрических сигналов на расстояние является правило согласования волновых сопротивлений: все элементы линии связи должны иметь одинаковое волновое сопротивление. При его нарушении происходит отражение сигнала от места контакта несогласованных элементов, при этом в следующий элемент попадает только часть энергии волнового сигнала, что приводит к постепенному затуханию волны в линии. Омическое сопротивление линии также вызывает затухание сигнала, поэтому его стремятся делать как можно меньше.

Волновое сопротивление линии равно корню квадратному из отношения распределенной вдоль линии индуктивности (погонной индуктивности) к распределенной вдоль этой же линии емкости (погонной емкости). Хотя волновое сопротивление рассчитывается исходя из реактивных сопротивлений, оно имеет активный характер. Физически волновое сопротивление линии показывает, какое эквивалентное сопротивление линия оказывает генератору. Это означает, что линия потребляет энергию от генератора.

,	(1)
,	(2)

где  характеризует степень затухания волны вдоль линии, а  - изменение фазы волны вдоль линии, L - погонная индуктивность линии [нГн/м], а С - погонная ёмкость линии [пФ/м].

Волновое сопротивление _В образовано реактивными, то есть не рассеивающими энергию элементами, и в некоторой степени характеризует скорость распространения сигнала v, так как

.

(3)

При наличии линии передачи с волновым сопротивлением _В условие передачи максимальной мощности требует равенства всех сопротивлений, то есть

.

(4)

Это есть так называемое условие согласования, то есть условие такого режима работы линии передачи, при котором равенство сопротивлений обеспечивает режим бегущей волны напряжения. При отличии сопротивлений возникает неоднородность, от которой происходит отражение волн, и часть энергии возвращается обратно к генератору. Условие равенства сопротивлений (а в общем случае - импедансов - полных комплексных сопротивлений) есть необходимое условие для максимальной передачи энергии в режиме бегущей волны. Кроме волнового сопротивления, линия, как упоминалось выше, характеризуется ещё и постоянной распространения .

Полные выражения для постоянной распространения  и комплексного волнового сопротивлениея Z_В имеют следующий вид.

,	(5)
,	(6)

где R – погонное «омическое» сопротивление кабеля, g – погонная проводимость материала изоляции (рис.1).

В идеальной линии передачи, то есть без потерь энергии, распространяются только волны, в которых векторы напряженностей электрического и магнитного полей строго поперечны. При теоретическом описании процессов в длинных линиях благодаря квазистатической поперечной структуре полей можно оперировать не c напряженностями полей E и H, а c зарядами q, токами I и напряжениями V.

Распределения токов и напряжений в линии в зависимости от  и Z_В получают из решения телеграфных уравнений, которые для идеальной двухпроводной линии имеют следующий вид.

,	(7)
,	(8)

где z – координата вдоль длинной линии.

Общее решение телеграфных уравнений для L=const и C=const представляет собой суперпозицию волн тока и напряжения.

,

(9)

где k – координата вдоль длинной линии.

Является ли линия передачи «длинной» или нет, определяют, зная длину волны (или частоту) передаваемого сигнала. Определённая скорость волны и распределённые параметры линии передачи порождают особые ее свойства только в том случае, когда геометрические размеры элементов цепи становятся соизмеримыми с длиной электромагнитной волны. Например, при частоте 10 кГц длина волны в свободном пространстве равна 30 км (=c/f), то есть для таких частот 30 км - это «длинная» линия с распределёнными параметрами. А при частоте 10 ГГц (обычная частота современных СВЧ систем) длина волны равна 3 см в вакууме, то есть при =1. Микрополоски и кабели могут быть размещены в диэлектрической среде с высокой относительной диэлектрической проницаемостью  (от 2 до 100). Длина волны в диэлектрической среде зависит от ее относительной диэлектрической проницаемости следующим образом.

,	(10)
,	(11)

В результате эффект «длинных» линий может проявиться таким образом, что отрезки уже миллиметровой длины станут «длинными» линиями.

Полное комплексное сопротивление нагрузки может быть

• чисто активным, равным или не равным волновому сопротивлению _B;

• смешанным;

• чисто ёмкостным;

• чисто индуктивным.

Для каждого случая линия будет работать в разных режимах передачи энергии.

Наиболее важными являются режимы согласования Z=Z_Н=R_Н и рассогласования Z≠ Z_Н=R_Н. В последнем случае падающая волна от генератора порождает отражённую волну от нагрузки и величина амплитуды отраженной волны зависит от разности величин сопротивлений и характеризуется коэффициентом отражения .

,

(12)

Если Z_Н=R_Н=_B, то =0 и реализуется режим бегущей волны. А если R_Н≠_B, но R_Н≠0 и R_Н≠∞ то имеет место режим смешанных волн, когда происходит суперпозиция отражённой и падающей волн, что порождает стоячую волну.

Из режимов рассогласования наиболее интересны следующие режимы:

• режим короткого замыкания (КЗ), то есть Z_Н=0 и =-1;

• режим холостого хода (ХХ), то есть Z=∞ и =1.

Таким образом, в этих режимах отраженные волны имеют ту же величину, что и падающие, причем при разомкнутой линии (ХХ) - без перемены знака напряжения, а при замкнутой линии (КЗ) – с переменой знака напряжения.

3. Методика измерений

Подготовка к работе

Блок-схема измерительной установки представлена на рис.1. Импульсный сигнал с генератора импульсов 1 по кабелю “0” поступает на вход осциллографа 2. К этому же входу осциллографа будет подключаться в первой части работы кабель “5 м”, а во второй части работы последовательно будут подключаться кабели “I”, “II”, “III” и т.д.

• Включите осциллограф и генератор и дайте им прогреться в течение не менее 10 минут.

• Соедините кабелем “0” выход генератора с входом осциллографа.

• Установите частоту импульсного сигнала на выходе генератора в диапазоне от f=1 МГц до f=5 МГц, амплитудой U около 200 мВ и длительностью t не более 8 нс.

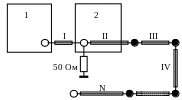
Рис.1. Блок-схема измерительной установки.

1 – генератор импульсов; 2 – осциллограф; “0” – соединительный кабель между генератором и осциллографом; “I”, “II”, “III”, … “N” – кабели для исследования прохождения сигнала.

• Настройте осциллограф и получите на его экране последовательность импульсов, как это показано на рис. 2.

• Измерьте с помощью осциллографа период следования импульсов, который должен быть равен

.

(13)

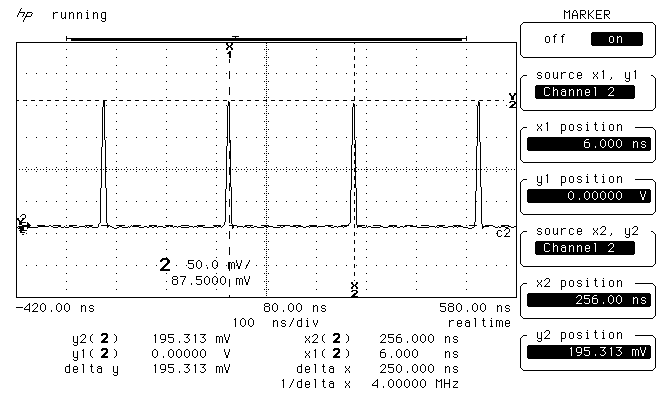
Рис.3. Осциллограмма последовательности импульсов частотой 4 МГц

Проведение измерений

1. Ознакомление с распространением электромагнитных волн в длинной линии. Нахождение коэффициента отражения и коэффициента затухания.

1. Подключите к входу осциллографа кабель длиной 5 м, являющийся линией задержки импульсного сигнала. Убедитесь, что если к выходу кабеля подключено сопротивление нагрузки, равное его волновому сопротивлению (в нашем случае R_Н=50 Ом), то отраженных волн в линии не возникает, и вся мощность поглощается нагрузкой.

Если же сопротивление нагрузки отличается от волнового сопротивления, то в линии возникают отраженные волны, которые возвращаются на вход осциллографа. Пройденный путь импульсного сигнала по линии задержки s и время задержки импульса t равны

,	(14)
	(15)

где l – длина кабеля, а v – скорость распространения электромагнитных волн по кабелю.

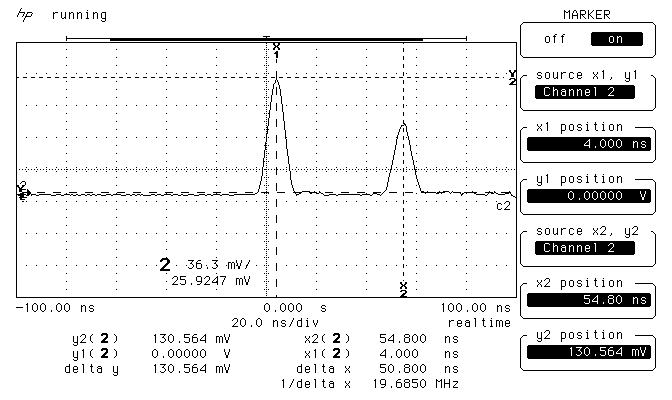
Рис.3. Осциллограмма основного и отраженного импульсов на экране осциллографа

Получите на экране осциллографа вместе с основным импульсом, приходящим от генератора, отраженный импульс в двух предельных случаях:

• в случае разомкнутой линии, если сопротивление нагрузки R_Н=∞ (режим холостого хода), как это представлено на рис.3;

• в случае короткозамкнутой линии, если сопротивление нагрузки R_Н=0 (режим короткого замыкания).

  2. Измерьте амплитуды А₀ и А_r основного и задержанного сигналов в обоих случаях. Если импульс направлен вниз, то амплитуда его отрицательна. Вычислите в обоих случаях коэффициент отражения  по следующей формуле.

,

(16)

3. Используя формулу для связи между коэффициентом отражения и нагрузками на входе линии задержки Z_B=50 Ом, и на конце линии задержки Z_H

,

(17)

где  - коэффициент затухания, вычислите коэффициенты затухания  в обоих случаях и сравните их величины.

2. Определение скорости прохождения импульса напряжения по кабелю и скорости света в вакууме.

1. Отсоедините кабель длиной 5 м от входа осциллографа. Измерьте длину кабеля «I» l=l₁. Подключите его к входу осциллографу и получите на экране осциллографа вместе с основным импульсом отраженный импульс, как это представлено на рис.2.

Измерьте время задержки t=t₁ между основным и отраженным импульсами в секундах. Пройденный путь сигнала по линии задержки равен s=s₁=2l₁. Запишите значения l=l₁, s=s₁ и t=t₁ в следующую таблицу.

Таблица

№пп	l, м	s, м	t, с

2. Измерьте длину кабеля «II» l=l₂. Подключите второй кабель “II” последовательно к кабелю “I” и снова измерьте время задержки t=t₂ между основным и отраженным импульсами. Пройденный импульсом путь по кабелю s равен s=s₂=2(l₁+ l₂). Запишите значения l=l₂, s=s₂ и t=t₂ в таблицу.

3. Присоедините кабель «III» последовательно к кабелю «II». Опять измерьте время задержки t=t₃ между основным и отраженным импульсами. Пройденный импульсом путь по кабелю s равен s=s₂=2(l₁+ l₂+ l₃). Запишите значения l=l₃, s=s₃ и t=t₃ в таблицу.

4. И так далее. По мере удлинения линии задержки, заполните таблицу со значениями пройденного пути s и времени сигнала t по линии задержки. Затем постройте по точкам график зависимости пройденного пути от времени s=f(t). Постройте линейную регрессию, то есть аппроксимируйте полученную зависимость линейной функцией.

.

(18)

5. Определите по графику скорость прохождения импульса по кабелю v в м/с. Рассчитайте относительную погрешность определения скорости прохождения импульса v/v.

.

(19)

Скорость прохождения импульса по кабелю определяется скоростью света в вакууме с и относительной диэлектрической проницаемостью материала заполнения кабеля ε.

,

(20)

6. Определите относительную диэлектрическую проницаемость материала заполнения кабеля  (значение скорости света в вакууме c=2.9979·10⁸ м/с). Рассчитайте относительную погрешность определения скорости прохождения импульса по кабелю v/v иотносительную погрешность значения диэлектрической постоянной /, а также относительную разницу между вычисленным значением  и его истинным значением, считая, что материал заполнения кабеля – полиэтилен, у которого =2.3.

Завершение измерений