Ryady_voprosy_i_otvety

Ряды и преобразование Фурье

Опр. ЛП Х – ЛНП, если

1. 

2. 

3. 

Пример 1.

1. 

2. 

3. 

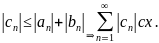
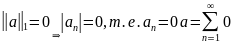
Пример 2.

Пример 3.

Пример 4.

мн-во кус.-непр. осредненных функций

Пример 5.

1. 

2. 

3. 

Пример 6.

Пример 7.

(под интегралом стоит не непр. ф-ия, для кот. нет теоремы)

1. 

Ф-ия разрывна на концах

2, 3 – сам-но, аналогично с примером 4

Пример 8.

Проверить, что это норма – самостоятельно

Пример 9.

Сам-но проверить, что это норма, след., ЛНП

Почему ? И почему рассм. их мы не будем?

Ответ.

Рассм. ряды

Такое мн-во обозначают . Мы рассмотрели . Непросто доказать, что

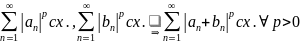
(это справедливо, но доказать трудно даже что это ЛП, поэтому такие вещи мы не рассм.)

Введем норму

Будем рассм. p=1

Аналогично с ф-иями.

Можно рассм.

Последовательности и ряды в ЛНП

Опр. Посл.

Опр.

Опр. Мн-во

Т1. Сх. посл-ть имеет ед. предел.

Док-во: сам-но

Т2. Сх. посл-ть ограничена.

Док-во: сам-но

Т3. (Арифм. св-васх. посл.)

Пусть

1. 

2. 

3. – непр. нормы

Док-во:

1. Сам-но

2. Т.к.

3. 

Опр.

(Система ЛНЗ – любая конечная подсистема ЛНЗ)

В опр. не исп. понятие нормы, поэтому оно годится и просто для любого ЛП.

Опр. ЛНП Х наз. беск.-мерным, если

Опр.

Опр. X – беск. ЛНП.

Отрицание ЛНС:

(найдется хотя бы одно )

два разных разложения

Опр.

Сам-но установить, что

(Всё док-но в книге Горячева)

Опр. ЛНП Х наз. полным ЛНП (ПЛНП), если

Т4.

Док-во:

посл-ть в

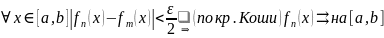
Сл.

Док-во: сам-но

(

Сравнение разных видов сходимости.

1. Равномерная сходимость, т. е. сходимость по норме

С[a,b], C^*[a,b], Q₀[a,b]

2. Поточечная сходимость, т. е.

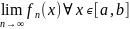
3. Сходимость в смысле L_p, т. е. ||f_n-f||_p→0, т. е.

→0

, т. е.

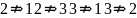
Опр. ЛП

1. ( 1^* )

2. 

3. 

4. 

Проверим св-ва нормы:

1.

2.

3.

Введенная таким образом норма называется нормой, соглас. со скал. произв.

Примеры евкл. пр-в.:

1. CL₂

(f,g)=

Убедимся, что это скал. произв.

1,2,3 св-ва пров. легко

4: (f,f)=

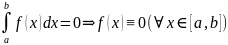
2. C^*L₂[ a,b]

(f,g)=

3. Q₀L₂[a,b]=

(f,g)= док-ся так же, как и в начале

(в трех примерах вводим стр-ру евкл. пр-ва и вводим спец. норму в нем)

Все, что уст-но для НЛП, применимо и для ЕП. Сохр. понятие полного ЕП.

Специфич. св-ва использования скалярного произв. надо доказать отдельно.

Т1.

Док-во:

+

Сл. (Счетная дистрибутивность скалярного произведения)

Док-во:

Y_n=y₁+ y₂+…+ y_n=

=

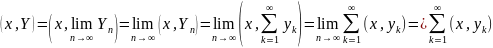
Опр.

Опр.

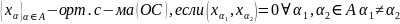
Опр.

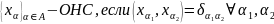
Условимся, что если не оговорено обратного, в ортог. с-ме нет нулевых элементов.

Убедимся, что ОС – ЛНЗ

0=

Построим (метод ортогонализ. Шмидта)

В конечном простр. этот процесс останавл., но мы взяли беск. с-му.

Примеры ортогональных и ортонормированных систем.

1. CL₂[-

Ортогонализуем с-му по Шмидту

degP_n=n - с-ма многочленов Лежандра

2. CL₂[- , C^kL₂[- , Q₀L₂[-

Рассм. с-му

Сам-но убедиться, что с-ма ортог., т.е. установить следующ.:

0=

(всевозм. скал. произв. разл. ф-ий)

Тогда:

3. CL₂[0 и Q₀L₁[0

0=

4. CL₂[0 C^*L₂[0 Q₀L₂[0

-ОС,

(f,g)=

5. CL₂[- ],

( )=

Опр. Если с-ма одновр. ортонормированна и явл. базисом, то она наз. ортонормированный базис.

Опр. Если с-ма одновр ортог. и базис, то она наз. ортогональный базис.

Ряды Фурье в евклидовом пространстве.

Т1.

Док-во:

Т1’.

Док-во: prav

Т2. . , причем “=”

Док-во:

-формула уклонения (квадрат величины приближения)

Т.е.

Т2’ prav

, причем “=” .

Док-во:

, ,

Т3 (Критерии ОНБ)

Пусть

1. 

2. 

3. 

эквивалентны.

Док-во: Установим, что 1

x=

Рассмотрим ²= (x,x)=( )=

счетная дистрибутивность скал. пр-я:

если сх. в евкл. пр.; , то (

=

2 (установим)

Формула уклонения

Т.е.

(док-ть)

Введем

Согл. ф-ле уклонения x= (ед-ть вытекает из Т1)

Сл .(Обобщенное равенство Парсеваля)

Пусть

Док-во: (x,y)=( )=дистр. ск. пр.=

Обобщ. рав-во Парсеваля м. записать, когда с-ма просто ортог-я:

x=

Обобщ. рав-во Парсеваля:

(x,y)=

Т4. (Полнота ортогон-го и ортонормир. базиса)

Пусть {e_n} – ОНБ ({g_n} – ОБ),

Док-во: (ОНБ – частн. случай ОБ докажем для ОБ)

#

Рассм. пр-во Q₀L₂[a,b]

Напишем обобщ. рав-во Парсеваля

Опр.

Предположим, что нек. тр. ряд

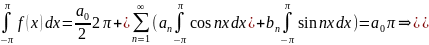
Найдем ост. коэфф-ты

Аналогично домножим ряд на sin nx

Опр. Если ф-ия , то тригонометрический ряд, в котором

Можем записать:

Лемма 1

Пусть ф-я Ф(x):

Док-во:

Лемма2.

Ф(х) инт. на [-l,l] , Ф(-х)=Ф(х)

Док-во:

Лемма3. prav

Ф(х) инт. на [-l,l] , Ф(-х)=-Ф(х)

Док-во:

Мы будем считать, что продолжена периодически с периодом (T=2 ) на

Рассм. част. сумму этого ряда (конечн. пер. многочлен)

=

Далее

Домножим

Если prav

Свойства ядра Дирихле

1. 

2. 

3. 

Св-ва вытекают из опр-я (можно док-ть)

Опр. Множество

не говорим того же) Назовем такие ф-ии кусочно- гладкими.

Лемма4. (Лемма Римана)

Док-во: Пусть

Ф-ия кус.-гл. её произв. тоже непр. на отрезке

При

Коэфф. Фурье должны стр. к нулю при . Если

Т1 . ( О поточечной сходимости ряда Фурье)

Док-во:

Ф-ла для ядра Дирихле

Рассм. на ост. отрезке. На

Т2. (О равномерной сходимости ряда Фурье)

Док-во: Ряд Фурье сходится поточечно к f(x)

Найдем коэфф.

|

Т3. (О почленном дифф. Ряда Фурье)

Пусть

Док-во:

Можем поставить в соотв. р. Фурье

По ф-лам из Т2

Мы можем получить коэфф., о сходимости ничего сказать не можем

Т4. (Порядок убывания коэфф. Фурье)

Чем больше у ф-ии произв-х, тем быстрее её коэфф. Фурье стремятся к нулю легче оценить ряд Фурье.

Док-во: