
STRS2_1
.docxМинистерство науки и высшего образования Российской Федерации
Федеральное государственное автономное образовательное учреждение высшего образования
ТОМСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ СИСТЕМ УПРАВЛЕНИЯ И РАДИОЭЛЕКТРОНИКИ (ТУСУР)
Кафедра радиотехнических систем (РТС)
Статистические свойства смеси регулярного сигнала и узкополосного стационарного гауссовского шума по дисциплине «Статистическая теория радиотехнических систем»
Выполнили:
Студенты гр. 122-1
________ Г.М. Дударев
________ Е.И. Гуляев
«__» ___________ 2025 г.
Проверил:
Инженер кафедры РТС
________ _________ И.А. Рыбаков
«__» ___________ 2025 г.
Томск 2025
ОСНОВНАЯ ЧАСТЬ
Формирование выборочных случайных последовательностей квадратурных составляющих смеси сигнала и гауссова шума
Сначала
были заданы следующие параметры (рисунок
1.1):
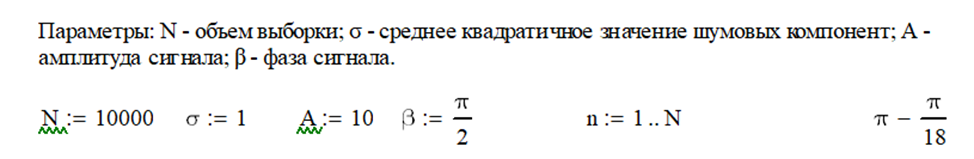
Рисунок 1.1 – Заданные параметры
После чего были получены две реализации смеси сигнала и белого шума, показанные на рисунке 1.2.
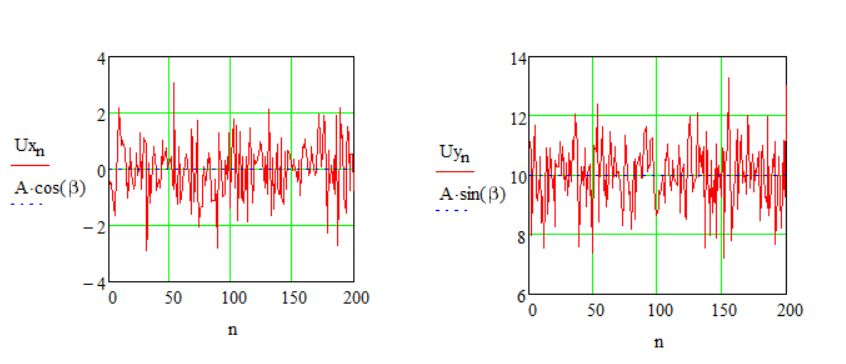
Рисунок 1.2 – Реализации смеси сигнала и белого шума
Реализации отличаются по фазе на 90 градусов, поэтому у функций отличается математическое ожидание (у левой функции минимум, а у правой - максимум). Среднеквадратическое отклонение на графиках соответствует заданному в параметрах σ = 1.
При изменении амплитуды сигнала A изменяется соответсвующее мат. ожидание.
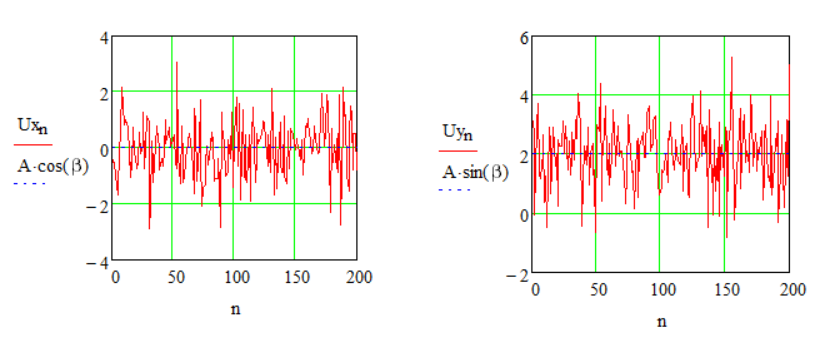
Рисунок 1.3 – Реализации при изменении амплитуды А
При изменении фазы β с 90 на 45 градусов изменяется соответсвующее мат. ожидание. (рисунок 1.4). Оно совпадает, поскольку значения синуса и косинуса при фазе 45 градусов равны.
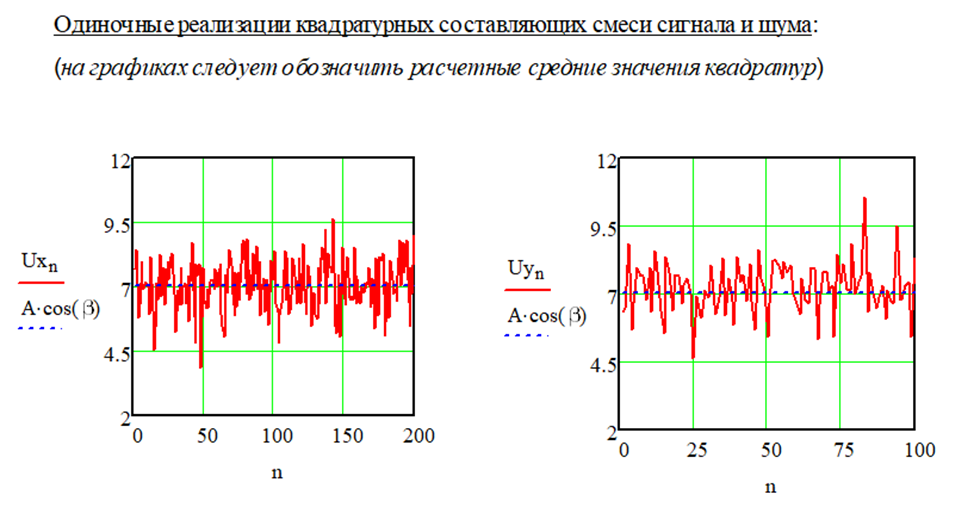
Рисунок 1.4 – Реализации при изменении фазы β
Формирование выборочных массивов огибающей и фазы смеси сигнала и шума
При установке параметров, показанных на рисунке 1.1 была получена реализации, показанные на рисунке 1.5. Также были на рисунке 1.1 приведены оценки параметров мат.ожидания и СКО.
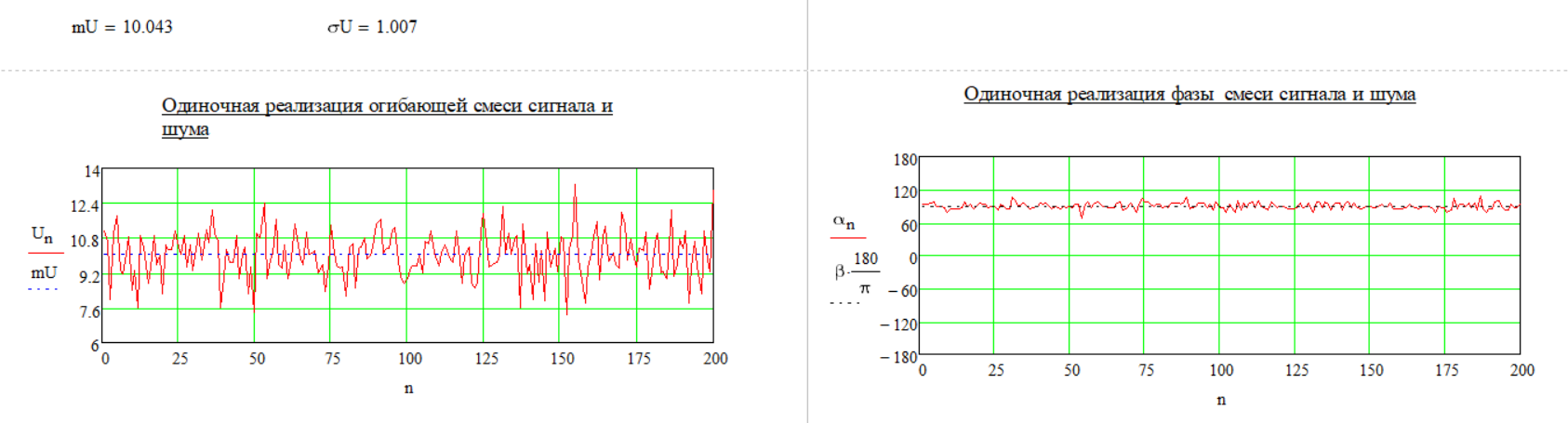
Рисунок 1.5 – Реализации огибающих
Из рисунка видно, что значение огибающая амплитуды сконцентрирована вокруг оценки, полученной ранее, а значение фазы - вокруг фазы, установленной в параметрах.
При уменьшении амплитуды А до значения 2 были получены следующие графики (рисунок 1.6):
![]()
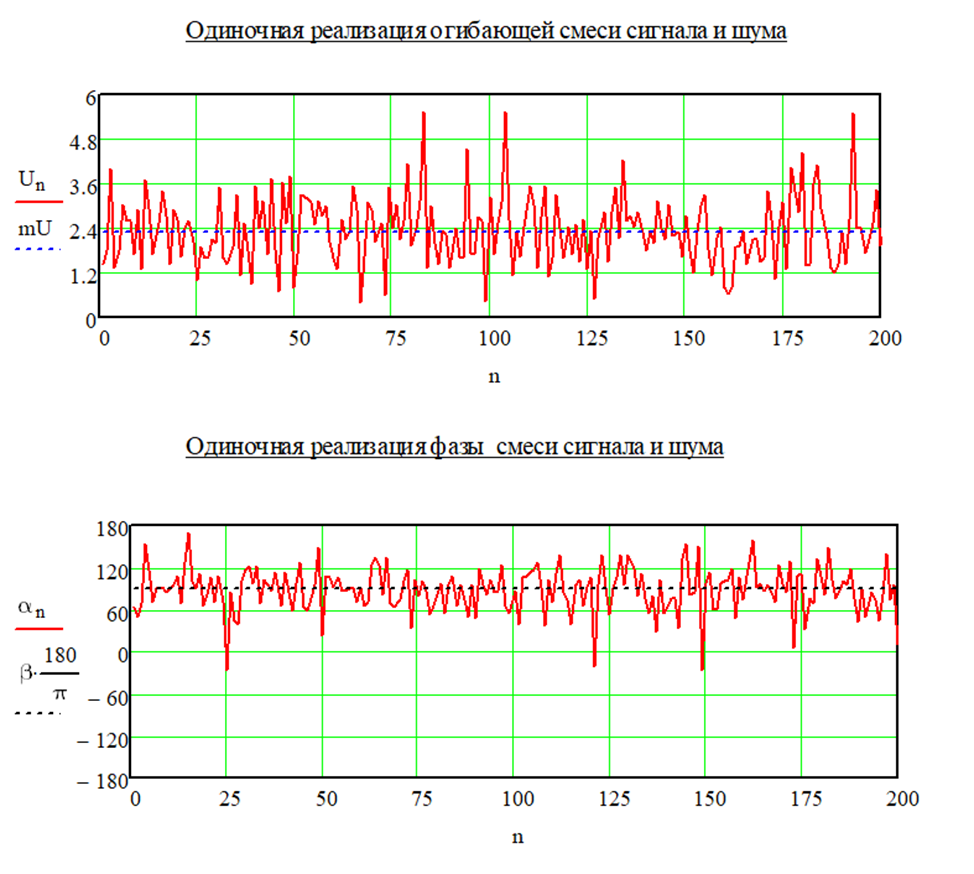
Рисунок 1.6 – Реализации огибающих при А = 2
Можно заметить, что изменились соответствующая оценка, а разброс значений фазы стал больше, т. к. соотношение сигнал-шум уменьшилось.
Затем значение СКО было увеличено до значения 10 и получены графики, показанные на рисунке 1.7.
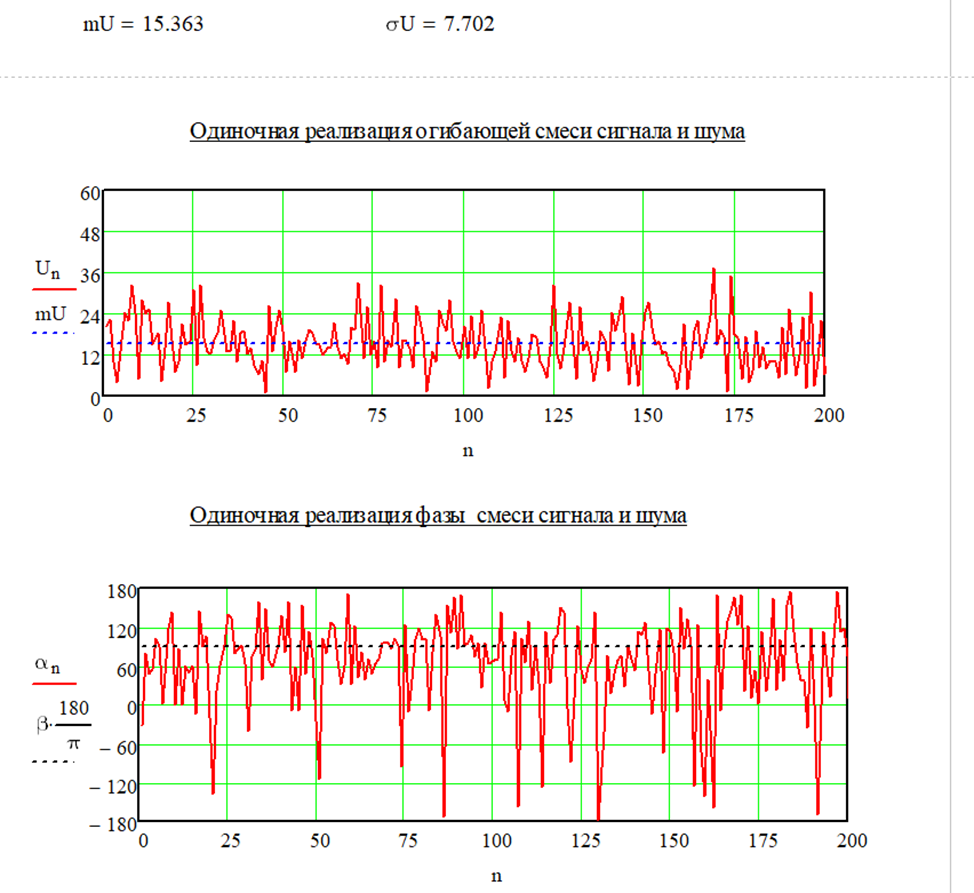
Рисунок 1.7 – Реализации огибающих при изменении СКО
Из рисунка видно, что при изменении СКО разброс значений увеличился, что привело к большему отклонению огибающей амплитуды и фазы, а также уменьшило точность оценки мат. ожидания и СКО амплитуды.
При изменении фазы бета до значения 45 градусов были получены следующие графики (рисунок 1.8):

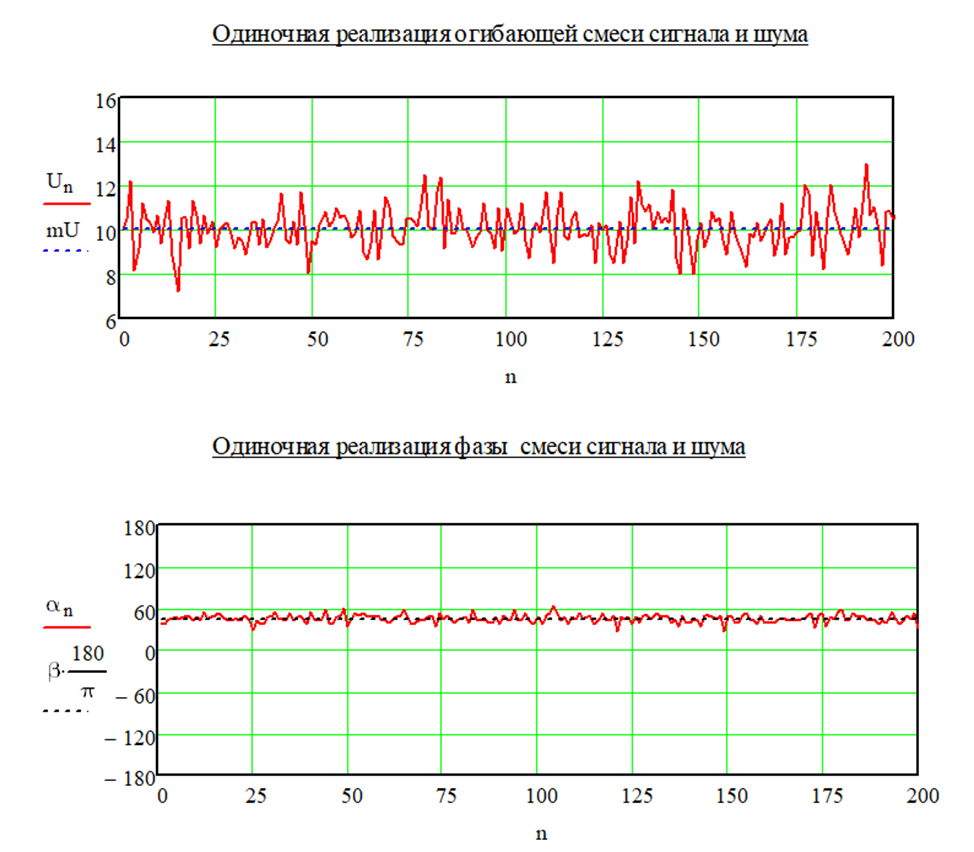
Рисунок
1.8 – Реализации огибающих при изменении

Из рисунка видно, что изменилось значение, вокруг которого концентрируется колебания фазы смеси сигнала + шум.
Блок анализа статистических свойств огибающей
При установке параметров, показанных на рисунке 1.1, была получена гистограмма, показанная на рисунке 1.9.
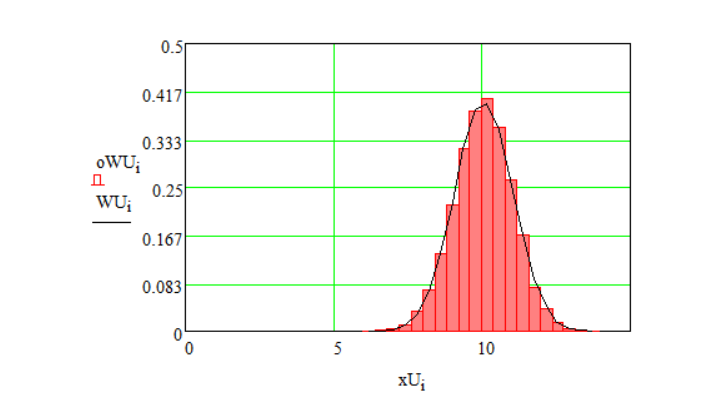
Рисунок 1.9 – ПРВ огибающей
При уменьшении амплитуды была получена гистограмма, показанная на рисунке 1.10.
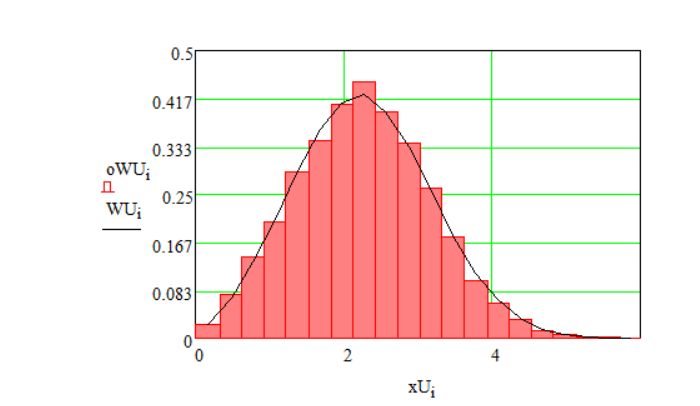
Рисунок 1.10 – ПРВ огибающей при А = 2
Из рисунка 1.10 видно, что гистограмма сместилось влево, поскольку значения теперь концентрируются вокруг амплитуды А = 2.
Также видно, что гистограмма стала шире из-за уменьшенного отношения сигнал-шум.
При увеличении СКО до значения 10 была получена гистограмма, показанная на рисунке 1.11.
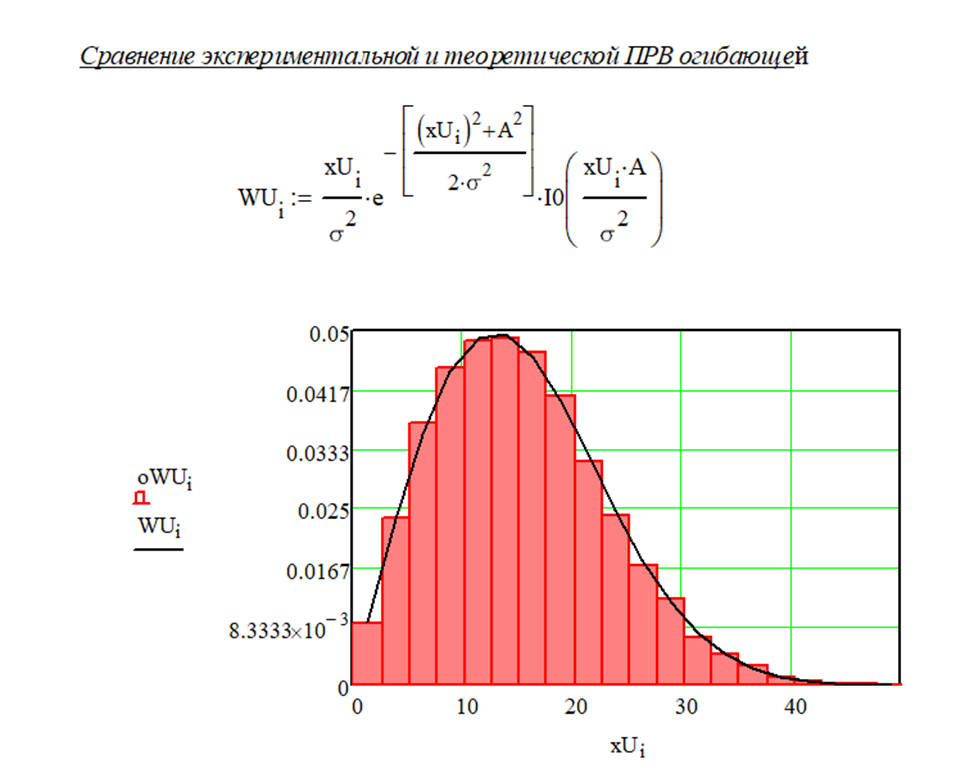
Рисунок 1.11 – ПРВ огибающей при изменении СКО
Из рисунка 1.11 видно, что гистограмма стала шире, высота столбцов уменьшилась, поскольку разброс значений стал больше.
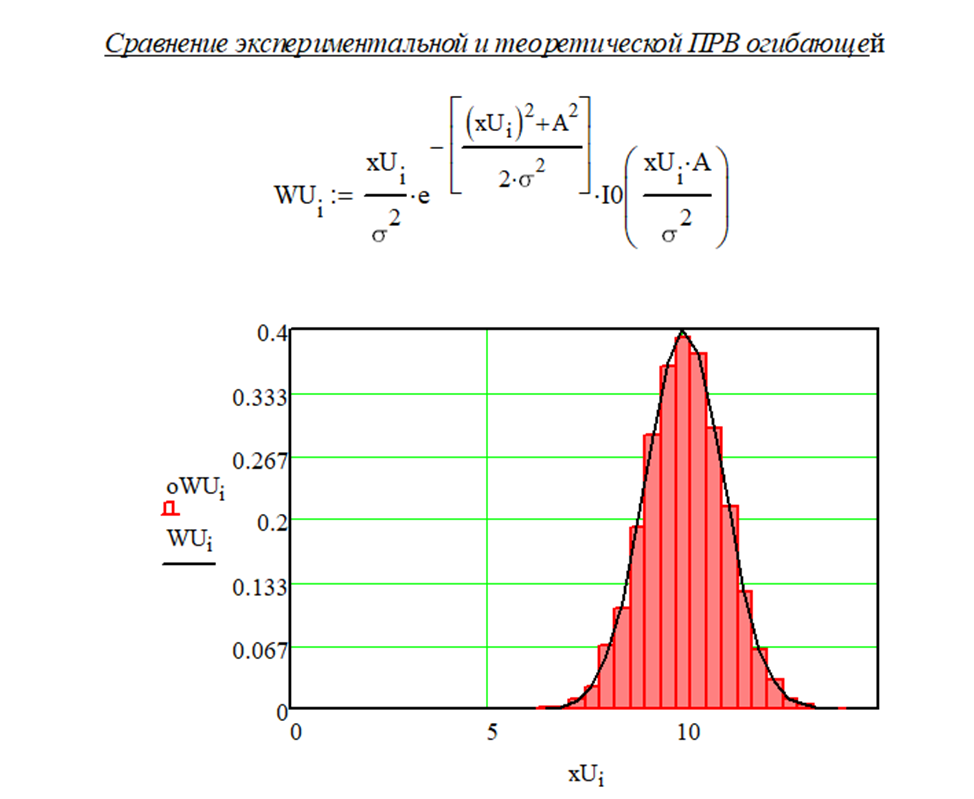
Рисунок 1.12 – ПРВ огибающей при изменении СКО
Изменение фазы на гистограмму не влияет.
Блок анализа статистических свойств фазы смеси сигнала и шума
При установке параметров, показанных на рисунке 1.1, была получена гистограмма, показанная на рисунке 1.13.
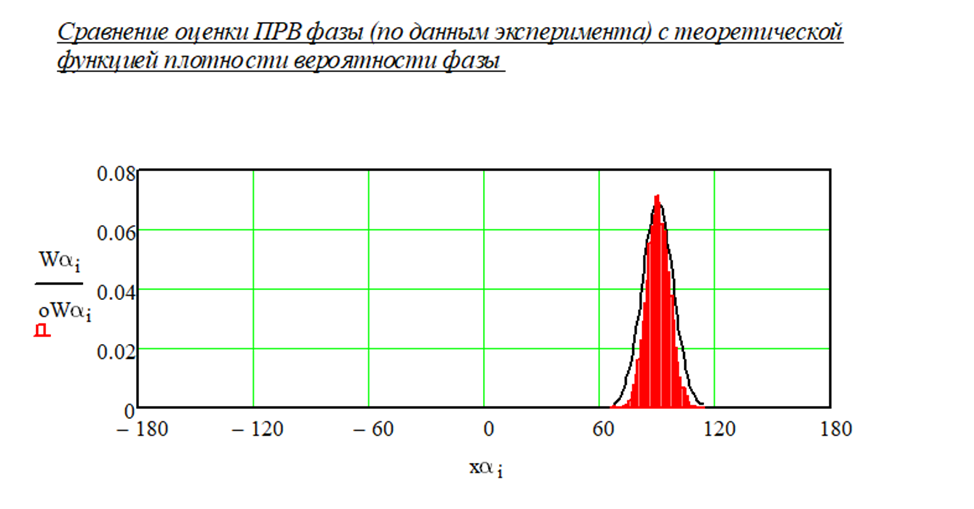
Рисунок 1.13 – ПРВ огибающей при изменении СКО
При уменьшении амплитуды до значения А = 2 была получена гистограмма, показанная на рисунке 1.14.
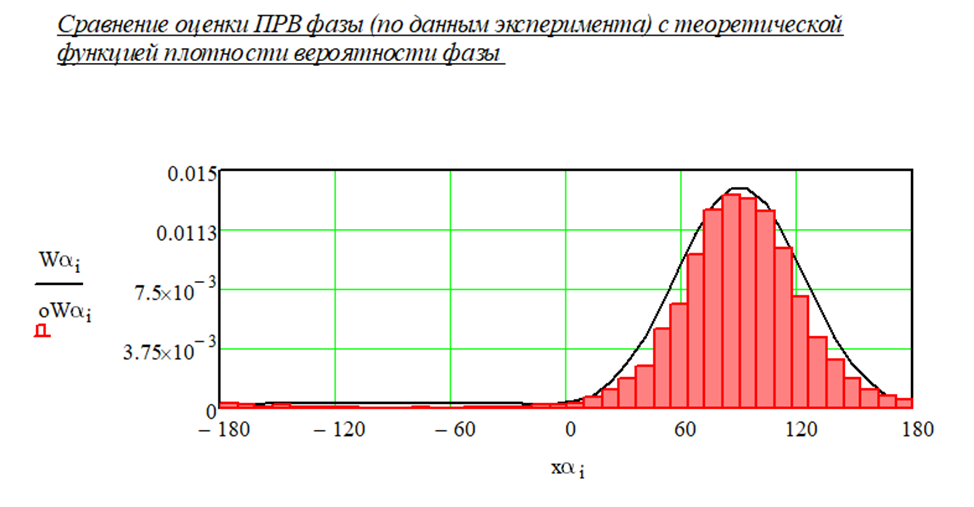
Рисунок 1.14 – ПРВ огибающей при изменении СКО
Из рисунка 1.14 видно, что гистограмма стала шире и ниже, поскольку, отношение сигнал/шум уменьшилось.
При увеличении СКО до значения 10 была получена гистограмма, показанная на рисунке 1.15.
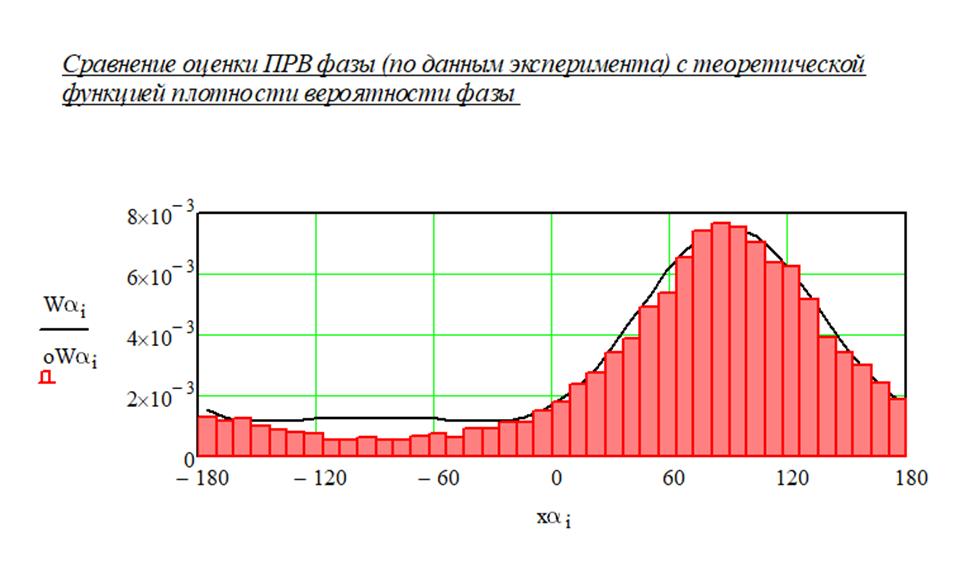
Рисунок 1.15 – Гистрограмма при СКО = 10
При увеличении СКО уменьшается отношение сигнал/шум, поэтому гистограмма стала шире и ниже.
При уменьшении фазы до значения 45 градусов была получена гистограмма, показанная на рисунке 1.16.
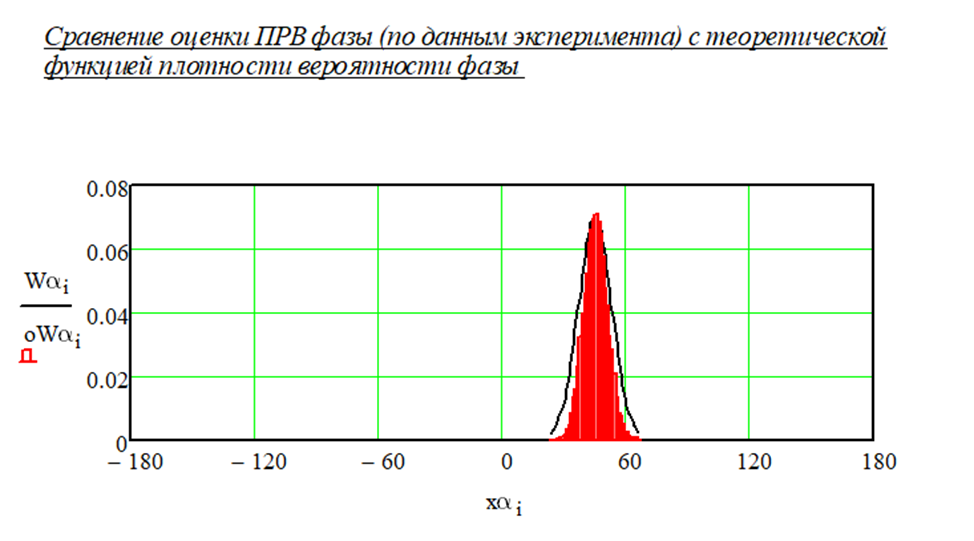
Рисунок 1.16 – Гистограмма при уменьшении фазы
Видно, что гистограмма теперь сосредоточена вокруг значения фазы 45 градусов.
Формирование дискретного радиосигнала
При установке параметров, показанных на рисунке 1.1, был получен график, показанный на рисунке 1.9.
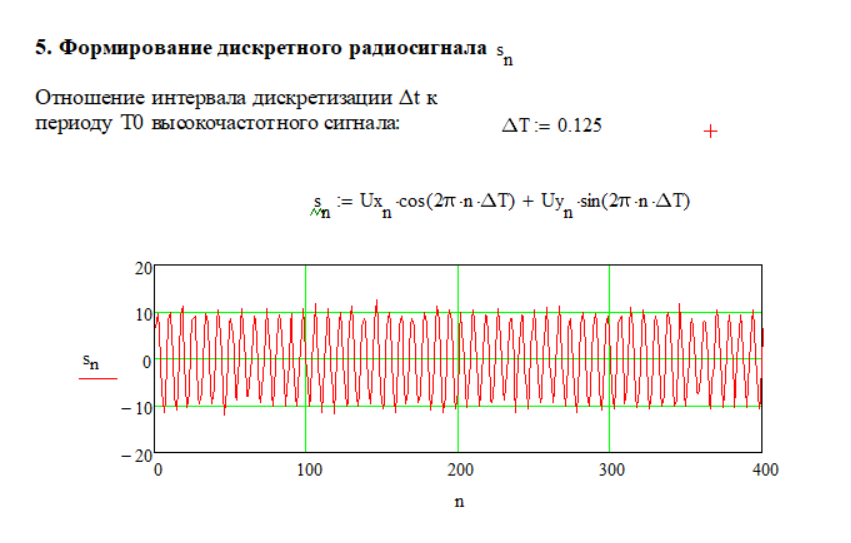
Рисунок 1.17 – Дискретный радиосигнал
При уменьшении периода дискретизации был получен график, показанный на рисунке 1.18.
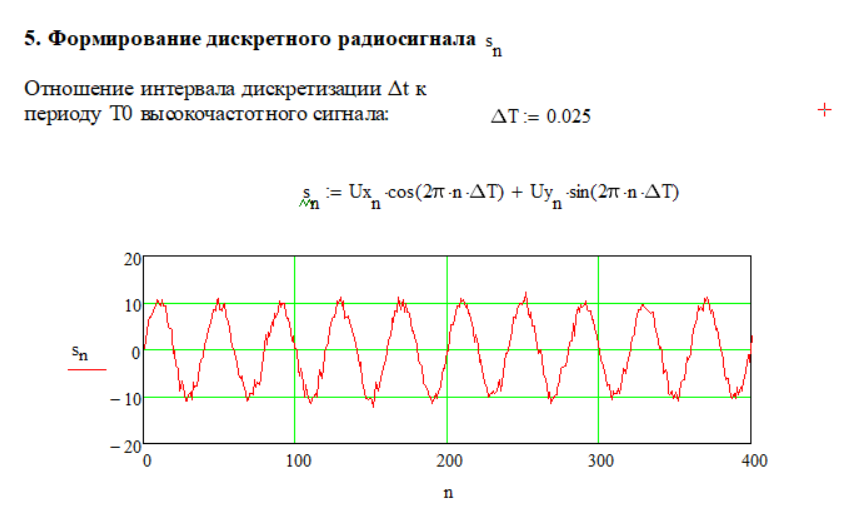
Рисунок 1.17 – Дискретный радиосигнал
Из рисунка 1.17 видно, что происходит алиасинг, поскольку частота дискретизации не удовлетворяет теореме Котельникова.
При увеличении отношения сигнал/шум с помощью увеличения амплитуды или уменьшения СКО, форма синуса приближается к идеальной, что видно на рисунке 1.18 (А = 15, СКО = 1):
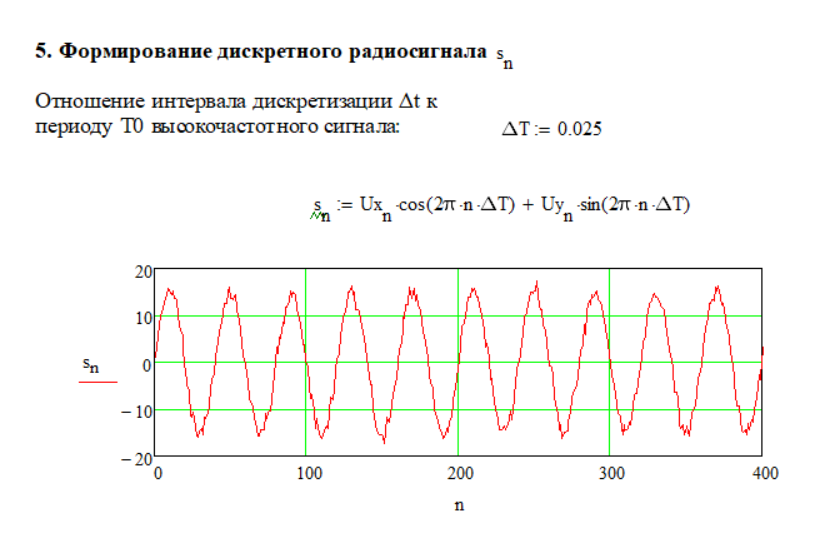
Рисунок 1.18 – Сигнал при измененном отношении с/ш
