
Лекции, Простокишин В.М. / Электронный формат / ДиИУ_2. Дифференциальные уравнения в частных производных 1-го порядка. Л. 06-07
.pdf
Л.06
Глава 2. Уравнения в частных производных (УрЧП) 1-го порядка
2.1. Первые интегралы систем ОДУ.
Определение.1. Непрерывно дифференцируемая в функция Ф( , , … , ) |
называется I-м интегралом системы |
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
̇= |
( , , … , ), = 1, , если для любого решения |
|
= ( ), … , |
( ) |
= |
|
( ) этой системы существует константа C такая, |
||||||||||||||||||||||||||||||||||||||||||||
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
что Ф( , ( ), … , ( )) = для ≥ 0. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Аналогично определяется I-й интеграл Ф |
( , … , |
|
) автономной системы ̇= |
( , … , |
), = 1, : Ф |
( ( ), … , |
( )) = . |
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
0 |
1 |
|
|
|||||||||||
Далее везде считаем |
( , |
|
, … , |
), = 1, и Ф( |
, … , |
|
) – непрерывно дифференцируемыми в . |
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
Теорема 1. (Критерий I-го интеграла). Для того, чтобы Ф( , … , |
) была I-м интегралом системы |
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
̇= |
( , … , |
|
), = 1, |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
необходимо и достаточно, чтобы выполнялось равенство |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
( , … , |
) |
Ф |
|
+ |
( , … , ) |
Ф |
|
+ + |
( , … , |
|
) |
|
Ф |
= 0 |
( , … , ) |
|
(1) |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
1 |
|
|
1 |
|
|
|
|
|
2 |
1 |
|
|
|
|
|
|
2 |
|
1 |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
Ф |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
(Коротко: ∑ |
|
( ) |
|
|
= 0 ). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
=1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Доказательство. Необходимость: ( |
|
Ф( )– I-й интеграл верно (1) ). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
Возьмем любое решение системы = ( ), = 1, . Так как Ф( )– I-й интеграл, то |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ф |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ф |
|
|
|
|
|
|
Ф( ( ), … , |
( )) = |
0 = |
Ф( ( ), … , ( )) = |
∑ |
( ( ), … , |
( )) • ̇ = ∑ |
|
( ( )) • |
( ( )) , ≥ 0. |
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
=1 |
|
|
|
|
|
|
|
|
|
|
|
|
=1 |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Если мы возьмем любую начальную точку (0) = 0, = 1, , то все сказанное верно для решения задачи Коши для системы̇= ( ), = 1, , с этим начальным условием, т.е. для:

|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ф |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(0) = ( |
0, … , 0) |
∑ |
( (0)) ∙ |
( (0)) = 0. |
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
=1 |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
В силу произвольности точки (0) = |
( |
0, … , 0) |
это означает выполнение равенства (1). |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Достаточность: ( Из справедливости (1) Ф( ) есть I-й интеграл системы ). |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
Дано: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(̃ , … , ̃ |
) |
Ф |
(̃ , … , ̃ |
|
|
) + |
|
(̃ , … , ̃ |
) |
Ф |
(̃ , … , ̃ |
) + + |
(̃ , … , ̃ |
) |
Ф |
(̃ , … , ̃ |
) = 0 |
(̃ , … , ̃ |
) |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
1 |
1 |
|
|
|
1 |
|
|
1 |
1 |
|
|
|
|
1 |
|
|
|
|
|
|
1 |
1 |
|
|
|
1 |
|
|
1 |
|
|
||||||||||||
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Тогда в качестве ̃ = |
(̃ , … , ̃ |
|
) можно взять точки любого решения системы, т.е. точки ( ) = ( |
( ), … , |
( )) |
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ф |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∑ |
|
( ( )) |
∙ |
( ( )) , ≥ 0. |
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
=1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
Но, так как это – решение, то ̇= |
( , |
, … , |
), = 1, и поэтому |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
Ф |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
∑ |
|
|
|
|
( ( )) ∙ |
|
|
|
= |
|
|
|
Ф( ( ), … , ( )) = 0 ≥ 0. |
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
=1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Таким образом, Ф( ( ), … , |
( )) = для ≥ 0, а это и есть определение I-го интеграла для системы ОДУ. |
||||||||||||||||||||||||||||||||||||||||||
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Замечание. Во всех определениях и теоремах можно заменить на область .

2.2. УрЧП. Основные понятия
Пусть = ( , … , |
) определена в некоторой области и имеет непрерывные производные ′ |
, ′ |
2 |
, … , ′ |
|
. Если |
|||||||||||
1 |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
||
считать, что ( |
, … , ) – неизвестная, то уравнение |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( , … , |
, , ′ |
|
, ′ |
|
|
, … , ′ |
|
|
) = 0 , |
|
|
|
|
(УрЧП-1) |
|
|
|
1 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
||
где – заданная непрерывная функция, называется уравнением в частных производных (УрЧП) 1-го порядка.
Решением этого УрЧП называется всякая непрерывно дифференцируемая в функция ( 1, … , ), обращающая уравнение в тождество.
Замечание. Аналогично определяются УрЧП более высокого порядка и их решения. При этом порядок уравнения – это порядок старшей производной, входящей в уравнение.
2.3. Линейное однородное УрЧП 1-го порядка
|
|
|
|
|
|
|
|
|
( , … , |
) |
|
||
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
∑ |
|
( , … , ) |
1 |
|
|
= 0 |
(1) |
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
=1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
где |
( , … , |
) = |
|
( ) – заданные функции (в ). |
|
|
|
|
|
|
|||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
Здесь, как и ранее: решением УрЧП (1) называется любая непрерывно дифференцируемая функция ( 1, … , ) (определенная в) , обращающая уравнение (1) в тождество.
Основные предположения:
А) ( 1, … , ) – непрерывно дифференцируемая функции (в );
Б) ∑ |
2 |
( |
, … , ) ≠ 0 |
|
|
|
1 |
|
|
=1 |
|
|
|
|
Сопоставим УрЧП (1) систему ОДУ вида:
̇ = |
( , … , ), |
|||
1 |
1 |
|
1 |
|
{ |
|
|
… |
(2′) |
̇ = |
|
( , … , ) |
||
|
|
1 |
|
|
Эта система называется системой ОДУ для характеристик УрЧП (1).
Систему для характеристик (2′) исключением можно свести к другой системе (записанной в симметричном виде):
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
1 |
= |
|
|
2 |
|
|
= = |
|
|
|
|
(2) |
|
( , … , ) |
|
( , … , |
) |
|
( , … , ) |
||||||||
1 1 |
|
2 |
|
1 |
|
|
|
|
1 |
|
|
|||
Система (2) состоит из ( − 1) уравнений и называется характеристической системой. |
|
|||||||||||||
Определение. Решения системы (2) называются характеристиками УрЧП (1). |
|
|
|
|||||||||||
Эти решения в параметрической форме: |
= ( ), … , |
|
= |
( ) |
являются решениями системы для характеристик (2′). |
|
||||||||
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
||

Л.07
Заметим важный факт. УрЧП (1) есть равенство из критерия 1-го интеграла для системы (2’):
|
|
|
|
|
|
|
|
|
|
( ) |
|
|
|
̇ = |
|
( , … , |
), = 1, … , |
∑ |
|
( ) |
= 0 |
||
|
|
|
|
|
|||||||
|
|
|
1 |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
=1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
т.е. ( , … , |
) есть I-й интеграл системы (2′). |
|
|
|
|
|
|
|
|||
1 |
|
|
|
|
|
|
|
|
|
|
|
Отсюда следует
Теорема 1. (о нахождении частных решений УрЧП).
Пусть ( , … , |
|
) |
– решение УрЧП (1), а |
( ), … , |
|
( )– характеристики (т.е. решения ОДУ (2′)). |
|||
1 |
|
|
|
|
1 |
|
|
||
Тогда ( ( ), … , |
|
( )) = ≥ 0 . |
|
|
|
||||
1 |
|
|
|
|
|
|
|
|
|
И обратно: если ( , … , |
|
)– I-й интеграл системы (2’) то это решение УрЧП (1). |
|||||||
|
|
|
|
1 |
|
|
|
|
|
Вывод: 1-й интеграл ( , … , ) системы ( ′) (или, что удобнее, системы (2) ), есть решение УрЧП (1).
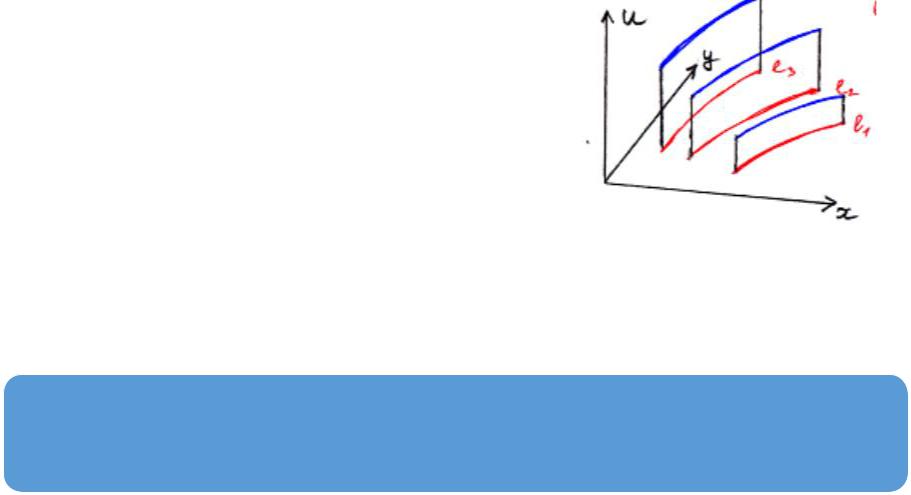
Теорема 1 устанавливает важный геометрический факт.
Пусть мы решаем УрЧП вида ( , ) |
|
+ ( , ) |
|
= 0. |
|
|
|
|
||
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
||
Находим его характеристики, решая ОДУ: |
|
|
|
|
|
|
|
|
||
̇= ( , ) |
|
|
|
= |
|
= ( ), = ( ). |
||||
{ ̇= ( , ) |
|
|
|
|
||||||
|
( , ) |
( , ) |
||||||||
Тогда для любого решения = ( , ) |
( ( ), ( )) = |
≥ 0 |
|
|||||||
Пусть 1, 2, 3 – различные характеристики.
Тогда вдоль них функция ( , ) постоянна.
Нечто подобное верно и во многомерном случае.
Таким образом, Теорема 1 позволяет найти частные решения УрЧП (1).
А как найти все возможные решения?
Теорема 2. Пусть выполнены основные предположения и заданы (n-1) штук первых интегралов системы (2):
|
|
( ) = , … , |
−1 |
( ) = |
в , ( = |
( , … , )) . |
|
|
1 |
1 |
−1 |
|
1 |
|
|
Если ( , … , |
)– любая непрерывно дифференцируемая функция (в −1) , то функция |
||||||
−1 |
|
|
|
|
|
|
|
= ( 1( ), 2( ), … , −1( )) |
есть решение УрЧП (1). |
|
|
|
|||

Доказательство. Найдем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
−1 Ψ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
∑ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
=1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
и подставим в УрЧП (1): |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
−1 |
Ψ |
|
|
−1 |
|
Ψ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
∑ ( ) |
|
= ∑ |
( ) ∑ |
|
|
|
|
|
= |
∑ |
|
|
|
|
|
∑ |
|
|
( ) |
|
|
|
|
= 0 |
|
(∑ |
( ) |
|
= 0, крит. I интеграла) ; |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
=1 |
|
=1 |
|
|
=1 |
|
|
|
|
|
=1 |
|
|
|
=1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
=1 |
|
|
|
|
|
|
|||||||||||
таким образом, есть решение УрЧП (1). |
|
Таким образом, есть решение. |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
Теорема 3. (О виде общего решения) Если I-е интегралы из теоремы 2 такие, что якобиан |
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
1 |
|
… |
|
|
1 |
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
2 |
|
|
|
|
|
−1 | |
|
|
|
|
|||||||
|
|
|
|
|
|
|
( , … , |
) |
|
|
|
|
|
|
|
2 |
|
|
2 |
|
|
|
2 |
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
| |
|
1 |
|
|
−1 |
|
| = |
|
|
|
|
|
|
|
|
|
|
|
|
|
… |
|
|
|
|
|
≠ 0 |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
( , … , |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
1 |
|
|
|
|
|
|
2 |
|
|
… |
|
|
−1 |
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
1 |
|
|
−1) |
|
|
|
… |
|
|
|
|
|
|
… |
|
|
… |
| |
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
−1 |
|
|
|
|
|
−1 |
|
… |
|
|
−1 |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
1 |
|
|
|
|
|
−1 |
|
|
|
|
|||||
в некоторой точке |
Х(0)((0), … , (0)) то для любого решения = ( ), = ( , … , ) |
УрЧП (1) существует |
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|||
функция ( , … , |
|
) |
– непрерывно дифференцируемая и такая, |
что в некоторой окрестности О(Х0) точки Х0 верно |
||||||||||||||||||||||||||||||||||||||||||
|
|
−1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
равенство ( ) = ( |
( ), … , |
|
|
( )) |
, = ( |
|
, … , |
). Без доказательства. |
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
1 |
|
−1 |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Замечание. Теорема 3 – это теорема о виде общего решения УрЧП (1). Фактически, она означает, что любое решение УрЧП выражается как суперпозиция независимых 1-х интегралов системы для характеристик с помощью некоторой непрерывно дифференцируемой функции .

Какие дополнительные условия надо поставить, чтобы найти определенное решение УрЧП (в данном случае – линейного однородного)?
Для ОДУ – это начальные условия задачи Коши ′ = ( , ), (0) = 0. А для уравнения |
∑ |
|
( ) |
|
= 0 ? |
|
|
||||||
|
=1 |
|
|
|
||
|
|
|
|
|
|
Рассмотрим это на примере n =2:
( , ) |
|
+ ( , ) |
|
= 0, |
где ( , ), ( , )– непрерывно дифференцируемые функции в 2 и 2( , ) + 2 ( , ) > 0 в 2 . |
|||||||
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|||
Уравнение для характеристик: |
|
|
|
|
|
|
||||||
|
|
|
|
|
̇= ( , ) |
|
|
|
|
|||
|
|
|
|
|
{ ̇= ( , ) |
|
|
= |
|
. |
||
|
|
|
|
|
( , ) |
( , ) |
||||||
В силу наложенных условий, выполнена теорема существования и единственности решения системы ОДУ, т.е. через любую точку ( , ) 2 проходит единственная фазовая кривая = ( ), = ( ) – решение системы (т.е. единственная характеристика). Вдоль этих характеристик по Теореме 1 решение УрЧп (1) постоянно.
При этом по Теоремам 2-3 это решение имеет вид = ( ( , )), где ( , )– I-й интеграл решения системы:
( ( ), ( )) = = ≥ 0 = ( ( ( ), ( ))) = ( ) = .
Геометрически это значит следующее:
если мы
1) зададим кривую γ на плоскости ( , ) , не совпадающую с характеристиками,
и
2) зададим дополнительное условие ( , ) = ( , )( , ),
где ( , ) – непрерывно дифференцируемая,
то вдоль каждой характеристики, исходящей из точек кривой γ,
решение будет проходить на «высоте» ( , ).

Это показывает, как нужно ставить задачу Коши для УрЧП:
( , ) |
|
+ ( , ) |
|
= 0, |
|
|
|
||||
{ |
|
(3) |
|||
|( , ) |
= ( , )|( , ) |
||||
Справедлива следующая теорема:
Теорема 4. Пусть γ– кривая на плоскости XoY, не касающаяся характеристик УрЧП, а функция( , ) определена и непрерывно дифференцируема в некоторой окрестности кривой γ. Тогда
задача Коши (3) для УрЧП ( , ) + ( , ) = 0, имеет единственное решение в некоторой окрестности кривой γ. (Без.док).

