Добавил:

okley Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Национальный исследовательский ядерный университет (МИФИ)

Предмет:

Интегральные уравнения и вариационное исчисление

Файл:

ДиИУ_1_Элементы_теории_устойчивости_Л_02

.pdf

Скачиваний:

Добавлен:

01.06.2025

Размер:

1.02 Mб

Скачать

☆

	Л.02
1.2. Устойчивость решений линейной системы ОДУ
Важным частным случаем системы ОДУ является случай линейной системы:
Х̇= ( )X,	(6)
где ( ) – квадратная матрица n-го порядка с элементами ( ) в общем случае, зависящими от .

Предполагаем, что ( ) С([0, +∞)), следовательно выполнены условия теоремы	существования и
единственности решения задачи Коши для систем ОДУ. Очевидно, что = О – точка покоя системы (6).
Справедливы следующие теоремы об устойчивости положения равновесия = О системы (6).

Теорема 2. (Необходимое и достаточное условие устойчивости линейной систему ОДУ).

Положение равновесия = О линейной системы (6) устойчиво тогда и только тогда, когда все решения этой системы устойчивы.

При этом достаточность справедлива при условии, что, хотя бы одно решение системы (6) устойчиво.

Теорема 3. (Необходимое и достаточное условие асимптотической устойчивости линейной систему ОДУ).

Положение равновесия = О линейной системы (6) асимптотически устойчиво тогда и только тогда, когда все решения этой системы асимптотически устойчивы.

При этом достаточность справедлива при условии, что, хотя бы одно решение системы (6) асимптотически устойчиво.

Теорема 4. (Критерий устойчивости линейной систему ОДУ).

Справедливы два утверждения.

1)Точка покоя = О линейной системы (6) устойчива тогда и только тогда, когда каждое решение этой системы ограничено при ≥ 0.

2)Точка покоя = О линейной системы (6) асимптотически устойчива тогда и только тогда,

когда для всех решений ( ) выполняется

lim ‖ ( )‖ = 0.

→+∞

Кдоказательству теорем 2, 3, 4 вернемся позже.

1.3. Устойчивость по первому приближению

Рассмотрим частный случай линейной системы (6), когда матрица этой системы не зависит от , т.е. случай системы

с постоянными коэффициентами

= :

Х̇=

(7)

Пусть 1, … , –

собственные числа матрицы ,

1, … , –

максимальные размеры жордановых клеток,

содержащих, соответственно, 1, … , на диагонали. Всякое решение системы (7) может быть записано в виде

( )

= ∑

( )

(8)

−1

где

( )

( ) – векторные многочлены степени

− 1 ,

( + ),

= ,

= .

−1

Учитывая, для любого многочлена ( ) произведение ( ) → 0, когда → +∞ при < 0 имеем следующие

возможности в зависимости от спектра матрицы :

а)

Если = 1, … , s

< 0, то ( ) → при

→ +∞,

следовательно, в силу теоремы 4 точка покоя =

системы (7) асимптотически устойчива.

б) Если = 1, … , s

Re ≤ 0 и

(Re

= 0

= 1 ), то любое решение ( ) системы (7) ограничено,

следовательно, в силу теоремы 4 точка покоя = системы (7)

устойчива по Ляпунову.

в)

Если = 1, … , s

≤ 0

но

( Re

= 0

> 1),

то из (8) следует, что существуют решения

системы (7) в виде

( ) = ( )

( )(

)

−1

Если

= 0, то

= 1,

= 0

и ‖ ( )‖ → ∞ при

→ +∞.

Если

≠ 0, то рассмотрим

= 1, 2 … , тогда

= 1,

= 0

и ‖ (

)‖ → ∞ при → +∞.

Следовательно, в обоих случаях решение ( ) неограничено при → +∞ , а значит точка покоя = системы (7) в

силу теоремы 4 неустойчива.

г)

Если

> 0

то также существуют неограниченные решения системы (7),

следовательно, в силу

теоремы 4 точка покоя = системы (7) является неустойчивой.

Определение О.5. Система вида (1), в которой правая часть не зависит от
	( , ) ≡ ( ) = ( ( , … ,				), ( , … , ), … ,			( , … , ))
		1	1		2	1			1
называется автономной системой.
Достаточной информацией, которая позволяет дать полное исследование вопроса об устойчивости тривиального
решения линейной системы (7) с постоянными коэффициентами является информация о спектре матрицы .
Оказывается, что в случае { } ≠ 0 аналогичные условия справедливы и для нелинейной системы вида
		Х̇= + Φ( ; ),
		Х̇= + Φ( ; ),								(9)
где – постоянная матрица, а векторная функция
		‖ ( ; )‖ ≤ ‖ ( )‖ ≡ о(‖ ‖) при → О
		( ; ) С1([0, ∞)х ).

Здесь = {	\| ‖ ‖ ≤ } – шар с центром в точке = О радиуса . К виду (9) легко сводятся автономные системы

		Х̇= ( ),		( ) = ,		( ) С1(			)	(10)

путем разложения этой вектор-функции ( ) до первого порядка с остаточным членом в форме Пеано.
Теорема 5. (Об устойчивости по первому приближению). Рассмотрим систему (9). Пусть ( ; ) С1([0, ∞)х ) и
‖ ( ; )‖ ≤ ‖ ( )‖ . ‖ ‖ где ‖ ( )‖ → О при ‖ ‖ → О.
‖ ( ; )‖ ≤ ‖ ( )‖ . ‖ ‖ где ‖ ( )‖ → О при ‖ ‖ → О.					Тогда справедливы следующие утверждения:
1) Если для всех собственных чисел матрицы выполняются неравенства Re										< 0, то тривиальное решение системы

(9) асимптотически устойчиво;
2) Если собственное число		матрицы , для которого Re				0	> 0 , то тривиальное решение системы (9) неустойчиво;
	0					0
3) Если { } = 0 , то устойчивость или неустойчивость тривиального решения системы (9) зависит не только от


матрицы , но и от функции		Φ( ; ) , и данная теорема определенного ответа не дает.
Замечание. Смысл теоремы 5 заключается в том, что вместо исходной нелинейной системы рассматривается линейная
система, полученная линеаризацией исходной с точностью до бесконечно малых величин первого порядка малости и
исследуется точка покоя этой линеаризованной системы

1.4. Качественные исследования точки покоя простейшей системы ОДУ в случае n=2

Рассмотрим линейную систему с второго порядка постоянными коэффициентами



			x	a		x	a		x
			1	11		1	12		1

		x		a		x	a		x	2
			2		21 1			22		2
Точка ≡ (	,	) = (0 , 0) = O является точкой покоя этой системы.
1	2

В данном параграфе будем считать, что (−∞ , +∞). От системы (11) можно перейти к ОДУ первого порядка:

dx	a	x a		x
2	21	1	22	2
2	21	1	22	2
dx	a	x	a	x
1	11	1	12	2

(11)

(12)

Фазовая траектория системы (11) является интегральной кривой уравнения (12). При этом точка ≡ ( 1 , 2) = (0 , 0) для уравнения (12) является особой точкой , так как это – точка разрыва правой части уравнения (12) и в ней нарушается условие теоремы существования и единственности решения: точка покоя системы (11) является особой точкой уравнения (12).

Исследование точки покоя = O на устойчивость.

					h					h
						1						2
				1		1	,	h	2		1
1) Решение определяется собственными числами		,	матрицы системы и собственными векторами	h		1	,	h				2	.
1) Решение определяется собственными числами	1	2	матрицы системы и собственными векторами			1					h	2	.
						h					h
						2					2

		a				a		2
	det( A E) 0	11				12	0	2	trA det A 0
2) Характеристическое уравнение	det( A E) 0		a		a		0		trA det A 0
2) Характеристическое уравнение

				21	22

3) Собственные числа могут быть:

а) действительными, при этом по знаку – положительными, отрицательными, нулевыми;

салгебраической кратностью 1 или 2;

сгеометрической кратностью 1 или 2,

б) комплексными, при этом

с действительной частью – положительной, отрицательной или нулевой.

,
1	2

Каждому из указанных случаев соответствует свой вид решения, получающийся из общего, тип фазового портрета системы и тип устойчивости определяется собственными числами и собственными векторами системы

Рассмотрим различные возможные случаи.

I.	1 , 2 , 1 ≠	2	и одного знака.	Пусть 2	<	1 < 0,	т.е. \| 1\| <	\| 2\|.
Общее решение системы (11):

	x												h					h
														1						2
X		1		1	t	С		h	2	e	t	С		1	e	t	С		1		e	t
X			С h e		1	С	2	h		e	2	С		1	e	1	С			2	e	2
			1		1		2				2	1		1		1	2			2		2
		x												h					h
		2												2					2

(13)

	h					h
		1						2
1		1	,	h	2		1
h		1					h	2
		h
		2					2

– собственные векторы, отвечающие собственным числам 1, 2 , соответственно. Положение

равновесия асимптотически устойчиво.

Положим С1 = 0. Тогда	x		2	e	t	,	x		2	e	t
		С h			2			С h			2
	1	2	1				2	2	2

– параметрическое уравнение двух лучей, коллинеарных

собственному вектору

h	2
h

. Эти лучи «входят» в точку = O при +∞ , данная точка покоя асимптотически устойчива

(они приближаются к точке покоя = O как угодно близко).
Назовем эти лучи фазовыми траекториями II	(т.к. С2 ≠ 0, С1 = 0).
Аналогично, если положить С2 = 0. Тогда	x	1	t	,	x	1	t
		С h e	1			С h e	1
	1	1 1			2	2 2

и получаем еще два луча, коллинеарные

собственному вектору		h	1	также «входящие» в точку = O при											+∞
		h	,
			,

которые назовем фазовыми траекториями I (т.к. С1 ≠ 0, С2 = 0).
Пусть теперь С1 ≠ 0, С2 ≠ 0, тогда
										1	e 1t С				2	e 2t
X x1	С h1 e 1t С h2 e 2t С h1										e 1t С				h1	e 2t	,
	1		1	2	2		1 1			1			2 2		2		,
									h2						h2
x2
Откуда получаем:
						dx		С h1e 1t				С h			2e 2t
						2			1	1	2	2	2	2
						dx		С h1e 1t				С	h		2e 2t
					1				1	1	1	2	2	1

(приближающиеся к ней как угодно близко),

				1 t			2 t
x1		С1 1h1 e 1			С2 2 h1 e 2
							(14)
x С h1e 1t С h2e 2t
	2	1	1	2	2	2	2

(15)

Из уравнения (15) с учетом, того, что 2 − 1 < 0 следует, что

dx			1			2	e	(	)t		1
dx	С h			С h			e	2	1		h
								2	1
2	1	1	2	2	2	2					2
2	1	1	2	2	2	2					2
dx			1			2	e	(	)t	t	1
dx	С h			С h			e	2	1	t	h
								2	1
1	1	1	1	2	2	1					1

(16)

	dx	2	h1
lim			2
			h1
t dx
1			1
– фазовые траектории системы (11), отличные от траекторий I и II, «входят», в точку = O при				+∞, имея общую

касательную, коллинеарную вектору

h	1
h

, т.е. касаются фазовых траекторий I, отвечающих меньшему по модулю

собственному числу 1.

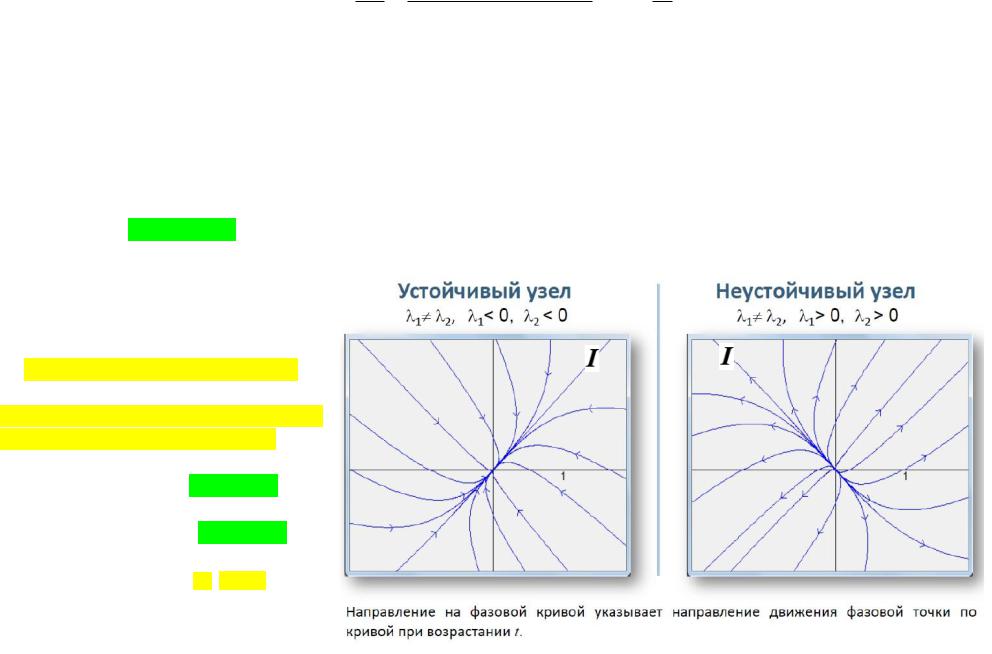
В случае 2 > 1 > 0 получаем аналогичную ситуацию, только с той разницей, что точка покоя = O является неустойчивой, и все фазовые траектории «выходят» из точки покоя.

Фазовый портрет случаях

1, 2 ,

1 ≠ 2,

1 2 > 0

Собственные числа действительные, неравные друг другу, одного знак

устойчивый узел, при 1 , 2 < 0

неустойчивый узел при 1 , 2 > 0 .

Рисунку соответствует | 1| < | 2|

Соседние файлы в папке Электронный формат

#
21.05.20253.53 Mб0ДиИУ_1_Теория_устойчивости_решений_задачи_Коши_Л_03_04_.pdf
#
01.06.20251.53 Mб1ДиИУ_1_Теория_устойчивости_решений_задачи_Коши_Л_05-1.pdf
#
21.05.20251.53 Mб0ДиИУ_1_Теория_устойчивости_решений_задачи_Коши_Л_05.pdf
#
01.06.20251.37 Mб1ДиИУ_1_Элементы_теории_устойчивости_Л_01-1.pdf
#
21.05.20251.4 Mб0ДиИУ_1_Элементы_теории_устойчивости_Л_01.pdf
#
01.06.20251.02 Mб1ДиИУ_1_Элементы_теории_устойчивости_Л_02.pdf
#
01.06.20253.53 Mб1ДиИУ_1_Элементы_теории_устойчивости_Л_03_05.pdf
#
01.06.20251.72 Mб1ДиИУ_2. Дифференциальные уравнения в частных производных 1-го порядка. Л. 06-07.pdf
#
21.05.20251.02 Mб0ДиИУ_2_Элементы_теории_устойчивости_Л_02.pdf
#
01.06.20256.81 Mб1ДиИУ_3_Ряды_Фурье.pdf
#
21.05.20252.27 Mб0ДиИУ_3_Теория_устойчивости_Л_03.pdf