Лекции, Простокишин В.М. / Электронный формат / ДиИУ_3_Ряды_Фурье
.pdf

Теорема (О поточечной сходимости тригонометрического ряда Фурье).
Если ( ) 1 2[− , ], то ее тригонометрический ряд Фурье
|
0 |
∞ |
|
|
|
|
|
|
( ) = |
+ ∑ |
|
+ |
|
||||
|
|
|
||||||
|
2 |
|
|
|
|
|
|
=1
сходится в каждой точке . При этом:
1)( ) = ( ) для любой точки непрерывности ( ) такой, что (− , );
2)( ) = 12 [ ( + 0) + ( − 0)] для любой точки разрыва такой, что (− , );
[Заметим, что по условию это всегда точки разрыва I рода]
3) (± ) = 12 [ (− + 0) + ( − 0)]
[Здесь ( ± 0) = |
lim ( ) – предельные значения ( ) в точке = ] |
|
→ ±0 |
Без доказательства.
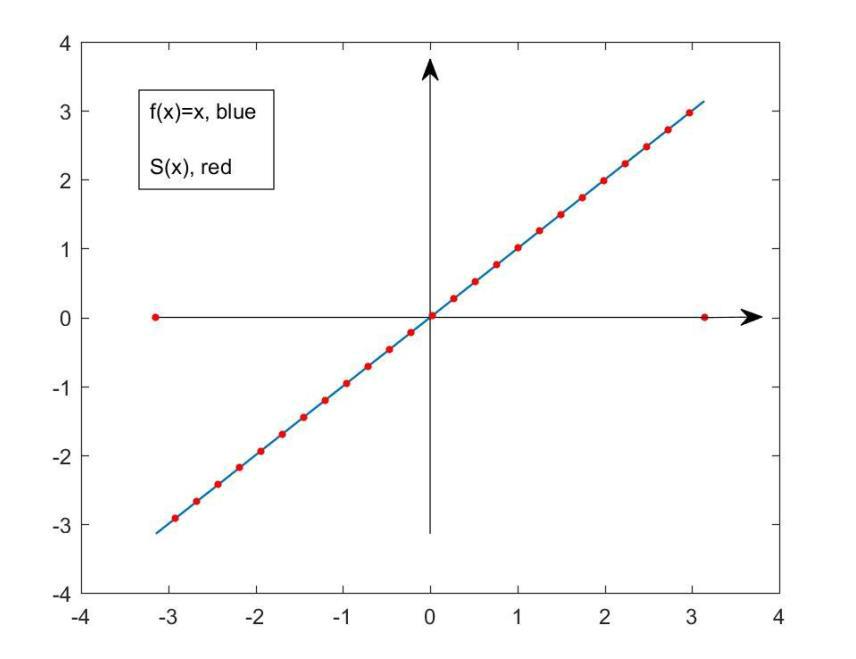
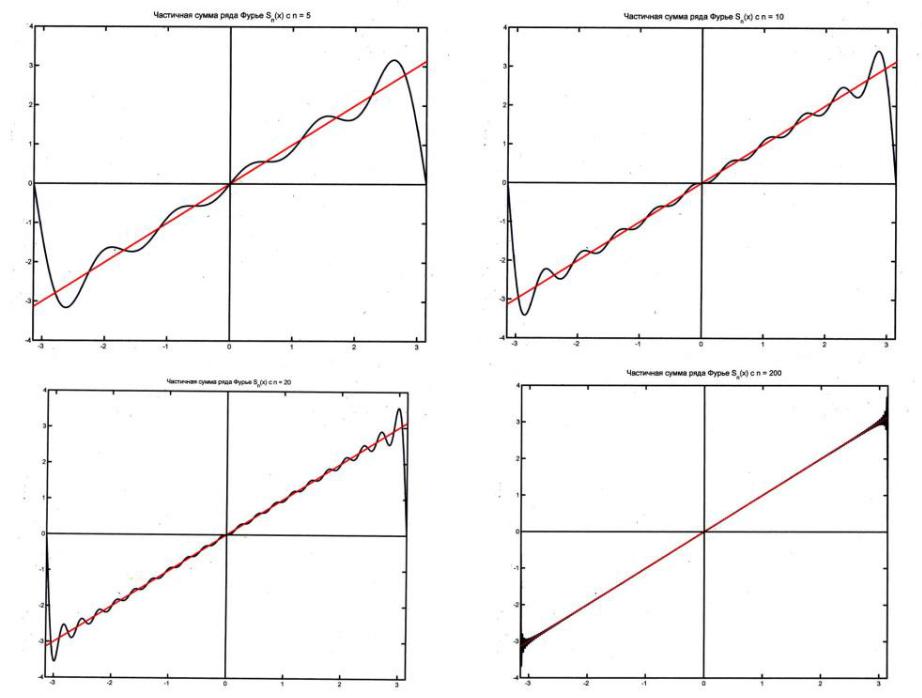
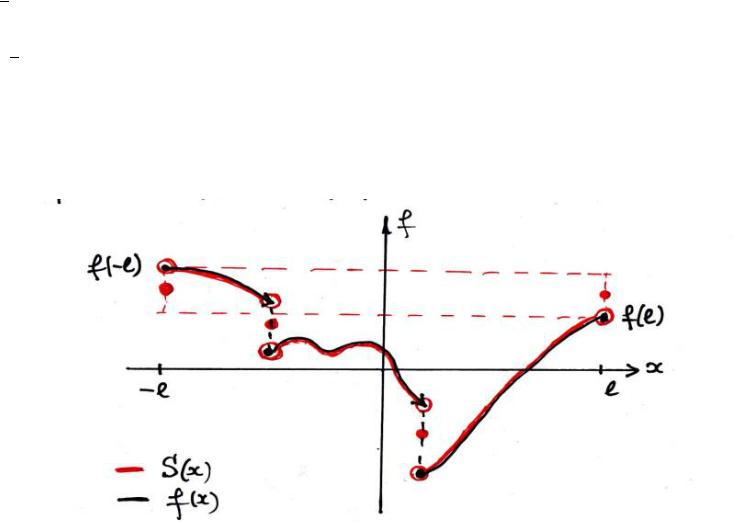
Прокомментируем это графически:
Очевидные следствия:
1)Если ( ) С[− , ] и ′( ) – кусочно-непрерывна на [− , ], то ( ) = ( ) для (− , ).
2)Если ( ) С[− , ] и ′( ) – кусочно-непрерывна на [− , ], и (− ) = ( ) , то ( ) = ( ) для [− , ].
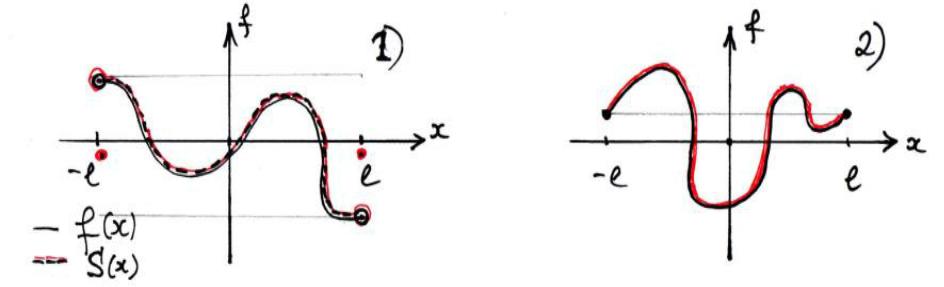
Графически это выглядит следующим образом:
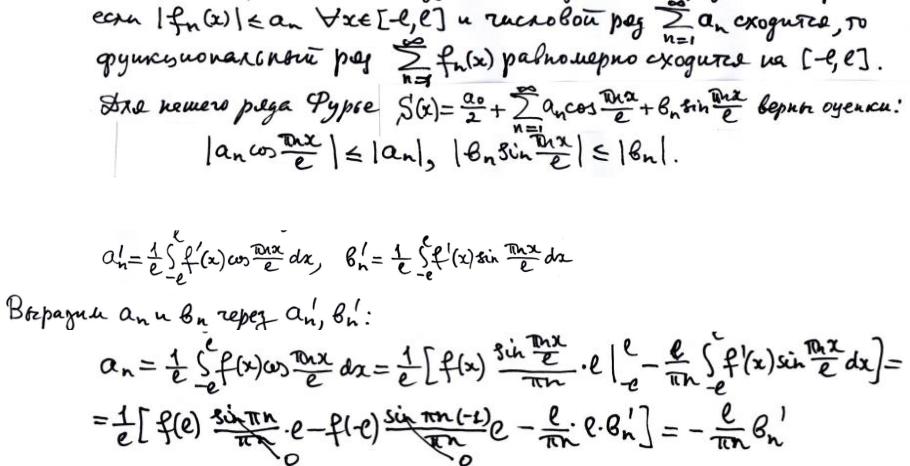
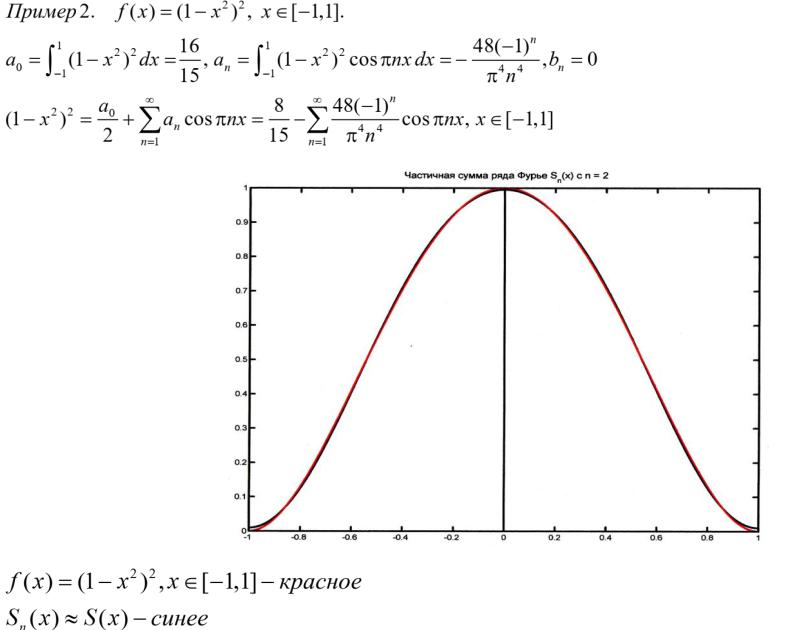
Теорема (О равномерной сходимости тригонометрического ряда Фурье).
Если: 1) ( ) [− , ] ∩ 1 2[− , ], т.е. ( ) непрерывна на [− , ] и имеет кусочно-непрерывную ′( ) на [− , ]; 2) (− ) = ( );
Тогда ( ) = ( ) всюду на [− , ] и ряд Фурье равномерно сходится к ( ) на [− , ], т.е.:
|
|
0 |
|
|
|
|
|
|
|
|
|
|
( ) = |
+ ∑ ( |
|
|
+ |
|
) |
( ) на [− , ]. |
|||
|
|
|
|
||||||||
|
2 |
|
|
|
|
|
|
|
|||
|
=1 |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
Доказательство. Используем мажорантный признак Вейерштрасса:
Поэтому Теорема будет доказана, если мы докажем сходимость ряда 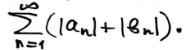
Обозначим