МИНОБРНАУКИ РОССИИ

Санкт-Петербургский государственный

электротехнический университет

«ЛЭТИ» им. В.И. Ульянова (Ленина)

Кафедра ИИСТ

отчет

по лабораторной работе №2

по дисциплине «Информатика»

Тема: Изучение основных возможностей текстового редактора MS WORD для подготовки текстовых документов.

Студентка гр. номер		ФИО
Преподаватель		Куракина Н.И

Санкт-Петербург

20__

Оглавление

Цель работы. 3

Задание. 3

Основные теоретические положения. 3

Результаты работы. 6

Выводы. 8

Цель работы.

Изучить основные возможности текстового редактора MS WORD для подготовки текстовых документов.

Задание.

1. Войти в систему

2. Вызвать для подготовки документа текстовый редактор MS WORD.

6. Создать новый документ

7. Настроить параметры страницы, задать шрифт, абзационный отступ и интервал в соответствии с правилами оформления

8. Ввести текст, данный преподавателем

3. Сохранить текст в папке «Text».

4. По результатам работы оформить отчет, содержащий пункты:

- Цель работы

- Задание

- Основные теоретические положения

- Результаты работы

- Выводы

Оформить разделы в виде заголовков и поместить после титульного листа оглавление.

5. В «Результаты работы» поместить набранный текст.

Основные теоретические положения.

1. Абзацный отступ – пробел в начале первой строки абзаца, подчёркивающий переход к новому фрагменту текста. Цель абзацного отступа – сделать членение текста на абзацы графически наглядным.

Абзацные отступы можно установить в окне Абзац.

Выделите нужный абзац(ы) или весь документ (клавиатурная комбинация CTRL + A) и нажмите правую кнопку мыши – пункт Абзац.

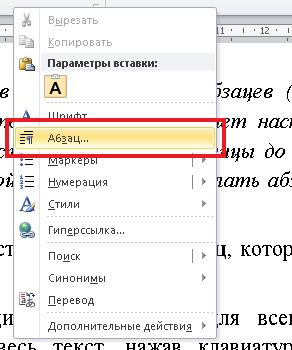
Рис.1. Изображение клавиши «абзац»

Далее откроется окно настройки абзацных отступов.

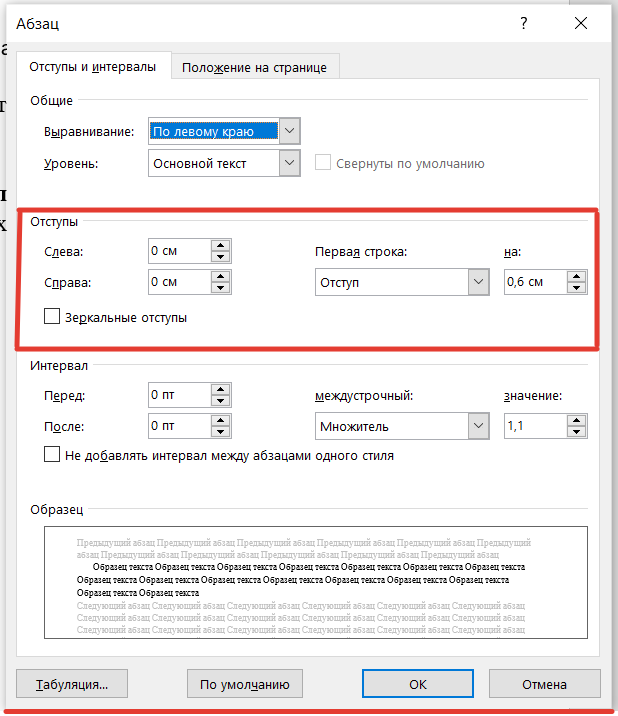
Рис.2. Изображение окна настройки абзацных отступов

Для установки полей отступа нужно установить значение отступа в сантиметрах в окне Абзац.

2. Межстрочный интервал – межстрочный пробел, расстояние между базовыми линиями соседних строк.

Для того, чтобы установить межстрочный интервал, нужно открыть окно Абзац (рис.2) , выбрать раздел интервал и ввести значения.

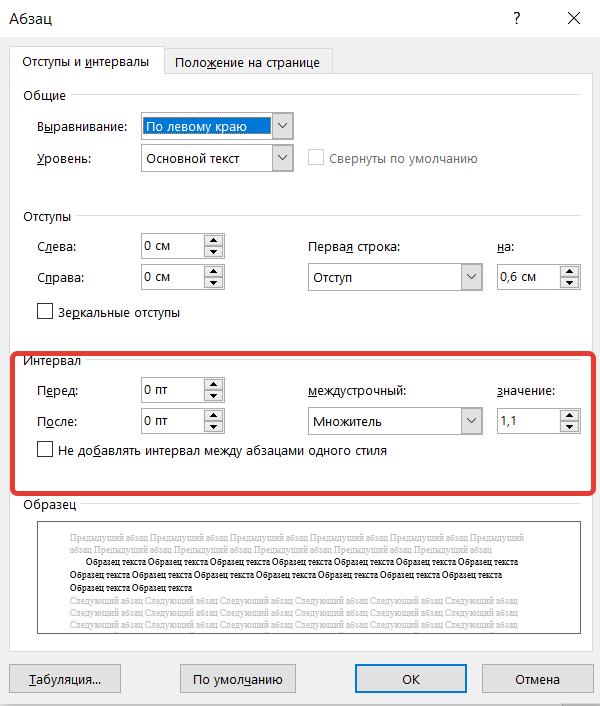
Рис.3. Изображение окна настройки межстрочного интервала

Результаты работы.

При дальнейшем изложении материала будет оговариваться возможность определения доверительного интервала в случае отличия распределения от нормального.

Для определения границ доверительного интервала погрешности результата измерений доверительная вероятность выбирается равной 0,95. В некоторых случаях ГОСТ 8.207 – 76 предусматривает и другие значения доверительной вероятности (0,99 и выше).

5.2 Определение оценки истинного значения измеряемой величины

5.2.1. Оценивание при известной дисперсии ряда измерений

Наилучшей оценкой истинного значения измеряемой величины при нормальном распределении результатов измерений является выборочное среднее ряда (5.1)

Дисперсия этой оценки

Служит одним из показателей точности измерений. Однако этот показатель содержит значительно меньше информации о погрешности чем вероятностно-зональный. Этим и вызвано стремление при обработке результатов измерений использовать именно последний. Но, естественно, что для расчета этого показателя надо иметь и больше априорной информации о погрешности. Для вероятностно-зонального показателя требуется знать закон распределения измерений.

Если ряд (5.1) имеет нормальное распределение

,

то оценка в силу устойчивости нормального закона при линейных преобразованиях также распределена по нормальному закону с математическим ожиданием и дисперсией .

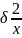Введем нормированную величину

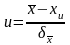
Нетрудно видеть, что имеет стандартный нормальный закон распределения, т.е. нормальный закон с нулевым математическим ожиданием и единичной дисперсией. Задавшись уровнем значимости α или, что тоже самое, доверительной вероятностью , найдем доверительный интервал, в котором будет находиться нормированная случайная величина на уровне значимости α или с доверительной вероятностью

Где и – квантили стандартного нормального закона распределения порядка 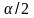и соответственно. Так как закон распределения центрирован и симметричен, то

откуда получаем неравенство

.

С учетом (5.3)

.

Последнее выражение удобно записывать в следующей символической форме

.

Где – доверительная граница случайной погрешности.

Получением численных значений (5.4) обычно и заканчивается обработка ряда прямых измерений при известной дисперсии ряда. Следует помнить только, что (5.4) имеет смысл при указании уровня значимости (или доверительной вероятности), для которого оно рассчитано.

Пример. При измерении входной емкости измерительного преобразователя были получены следующие значения (в пк : 10,1; 10,5; 11,2; 10,6; 11,1; 10,3; 9,5; 10,7; 9,1; 9,7; 8,9; 11,3; 10,9; 11,1; 10,8 .

Провести обработку ряда. Уровень значимости .

Дисперсия ряда измерений пкф .

Выводы.

Изучены основные возможности текстового редактора MS WORD, получены навыки работы с форматированием текста, редактированием абзацного отступа и межстрочного интервала, освоены возможности редактора формул Microsoft Equation 3.0.