
1 семестр ФИБС / Информатика / Лабораторные / ФИО_33_34
.docx
При дальнейшем изложении материала будет оговариваться возможность определения доверительного интервала в случае отличия распределения от нормального.
Для определения границ доверительного интервала погрешности результата измерений доверительная вероятность выбирается равной 0,95. В некоторых случаях ГОСТ 8.207 – 76 предусматривает и другие значения доверительной вероятности (0,99 и выше).
5.2 Определение оценки истинного значения измеряемой величины
5.2.1. Оценивание при известной дисперсии ряда измерений
Наилучшей оценкой истинного значения измеряемой величины при нормальном распределении результатов измерений является выборочное среднее ряда (5.1)
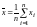
Дисперсия
этой оценки
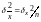
Служит одним из показателей точности измерений. Однако этот показатель содержит значительно меньше информации о погрешности чем вероятностно-зональный. Этим и вызвано стремление при обработке результатов измерений использовать именно последний. Но, естественно, что для расчета этого показателя надо иметь и больше априорной информации о погрешности. Для вероятностно-зонального показателя требуется знать закон распределения измерений.
Если ряд (5.1) имеет нормальное распределение
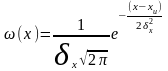 ,
,
то
оценка
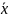 в силу устойчивости нормального закона
при линейных преобразованиях также
распределена по нормальному закону с
математическим ожиданием
в силу устойчивости нормального закона
при линейных преобразованиях также
распределена по нормальному закону с
математическим ожиданием
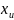 и дисперсией
и дисперсией
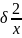 .
.
Введем нормированную величину
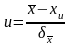
Нетрудно
видеть, что
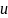 имеет стандартный нормальный закон
распределения, т.е. нормальный закон с
нулевым математическим ожиданием и
единичной дисперсией. Задавшись уровнем
значимости α или, что тоже самое,
доверительной вероятностью
имеет стандартный нормальный закон
распределения, т.е. нормальный закон с
нулевым математическим ожиданием и
единичной дисперсией. Задавшись уровнем
значимости α или, что тоже самое,
доверительной вероятностью
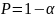 ,
найдем доверительный интервал, в котором
будет находиться нормированная случайная
величина
на уровне значимости α или с доверительной
вероятностью
,
найдем доверительный интервал, в котором
будет находиться нормированная случайная
величина
на уровне значимости α или с доверительной
вероятностью
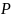
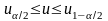
Где
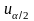 и
и
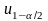 –
квантили стандартного нормального
закона распределения порядка
–
квантили стандартного нормального
закона распределения порядка
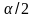 и
и
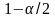 соответственно. Так как закон распределения
центрирован и симметричен, то
соответственно. Так как закон распределения
центрирован и симметричен, то
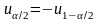
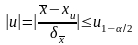
откуда получаем неравенство
 .
.
С учетом (5.3)

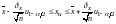 .
.
Последнее выражение удобно записывать в следующей символической форме
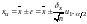 .
.
Где
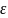 – доверительная граница случайной
погрешности.
– доверительная граница случайной
погрешности.
Получением численных значений (5.4) обычно и заканчивается обработка ряда прямых измерений при известной дисперсии ряда. Следует помнить только, что (5.4) имеет смысл при указании уровня значимости (или доверительной вероятности), для которого оно рассчитано.
Пример.
При измерении входной емкости
измерительного преобразователя были
получены следующие значения (в пк :
10,1; 10,5; 11,2; 10,6; 11,1; 10,3; 9,5; 10,7; 9,1; 9,7; 8,9; 11,3;
10,9; 11,1; 10,8 .
:
10,1; 10,5; 11,2; 10,6; 11,1; 10,3; 9,5; 10,7; 9,1; 9,7; 8,9; 11,3;
10,9; 11,1; 10,8 .
Провести обработку ряда. Уровень значимости .
Дисперсия
ряда измерений
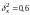 пкф
пкф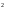 .
.
