29. Константа химического равновесия. Расчёт Кр и Кс.

Рассмотрим обратимую химическую реакцию общего вида, в которой все вещества находятся в одном агрегатном состоянии, например, жидком:

аA + вB D сC + dD,

где A и B – исходные вещества прямой реакции; C и D – продукты прямой реакции; а, в, с, и d – стехиометрические коэффициенты.

В начальный момент времени, когда концентрация веществ A и B наибольшая, скорость прямой реакции также будет наибольшей и по закону действующих масс равна

u_пр = k₁C_А^аC_В^в (6.1)

где k₁ – константа скорости прямой реакции.

С течением времени концентрация веществ A и B уменьшается, а, следовательно, уменьшается и скорость прямой реакции.

В начальный момент времени концентрация веществ C и D равна нулю, а, следовательно, и скорость обратной реакции равна нулю, с течением времени концентрация веществ C и D возрастает, а, следовательно, возрастает и скорость обратной реакции и она будет равна

u_обр = k₂C_C^сC_D^d (6.2)

где k₂ – константа скорости обратной реакции.

В момент достижения равновесия, концентрации принимают значение равновесных, а скорости равны между собой u_пр = u_обр, следовательно

k₁C_А^аC_В^в = k₂C_C^сC_D^d (6.3)

Перенесем константы скорости в одну сторону, а концентрации в другую:

(6.4)

Отношение двух постоянных величин есть величина постоянная, и называется она константой химического равновесия:

(6.5)

Константа равновесия показывает во сколько раз скорость прямой реакции больше или меньше скорости обратной реакции.

Константа равновесия – это отношение произведения равновесных концентраций продуктов реакции, взятых в степени их стехиометрических коэффициентов к произведению равновесных концентраций исходных веществ, взятых в степени их стехиометрических коэффициентов.

Способы выражения константы равновесия

Если концентрации веществ, участвующих в реакции, выражены в молярных единицах молярности , т.е. в моль/л, то она обычно обозначается Кс

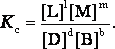
Для гомогенной газовой реакции константу равновесия удобнее выразить через парциальные давления веществ:

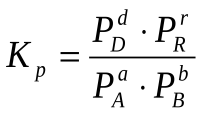
Иногда константу равновесия удобно выразить не через парциальные давления и концентрации, а через количества веществ: или через соответствующие мольные доли:

В общем случае константы равновесия Кс, Кр, Кn и К_N различны.

Константа равновесия и энергия изменения Гиббса.

Для реакции, протекающей в изобарно-изотермических условиях, в некотором неравновесном исходном состоянии энергии Гиббса или химические потенциалы реагирующих веществ и продуктов реакции в общем случае не одинаковы, их разность (ΔG_T) может быть рассчитана по уравнению:

где   — отношение парциальных давлений участников реакции в исходном состоянии в степенях, равных их стехиометрическим коэффициентам; R — универсальная газовая постоянная.

Это уравнение называют уравнением изотермы химической реакции. Оно позволяет рассчитать изменение энергии Гиббса при протекании процесса и определить направление протекания реакции:

при      — реакция идёт в прямом направлении, слева направо;

при      — реакция достигла равновесного состояния;

при      — реакция идёт в обратном направлении.

Стандартная константа равновесия связана со стандартной энергией Гиббса реакции соотношением:

Связь между Кс и Кр можно выразить соотношением:

Кр = Кс·(RT)^n ,

где n –изменение числа молей газов в результате реакции.

Например, при протекании реакции:

2СО + О2 = 2СО2

n = 1, следовательно, Кр = Кс·RT

Для получения зависимости константы равновесия К_р от температуры используем уравнение Гиббса — Гельмгольца:

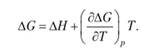(6.5)

Это уравнение отличается от известного уравнения для ΔG = ΔH - TΔS тем, что изменение энтропии ΔS в нем задано в неявном виде.

Учитывая то, что К'р в уравнении изотермы Ванг-Гоффа (6.4) не зависит от температуры (так как парциальные неравновесные давления участников реакции имеют определенные фиксированные значения), получим в результате дифференцирования этого уравнения

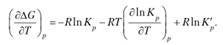
Подставим в уравнение (6.5) это выражение, а также уравнение изотермы Вант-Гоффа (6.4). После сокращения получим

(6.6)

Это уравнение называется изобарой химической реакции.

Аналогично получаем уравнение изохоры химической реакции:

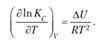(6.7)

Из этих уравнений очевидно, что, если тепловой эффект реакции имеет отрицательное значение (ΔН < 0 или ΔU < < 0), то величина константы равновесия с ростом температуры уменьшается, и равновесие смещается в сторону исходных веществ. Если ΔН > 0 (или ΔU > 0), то константа равновесия растет с увеличением температуры и равновесие смещается в сторону продуктов реакции. При ΔII = 0 (или ΔU = 0) величина константы равновесия не зависит от температуры. Эти же закономерности следуют из эмпирического принципа Ле Шателье.

Разделяя переменные в уравнениях (6.6) и (6.7) и интегрируя при ΔН = = const (или ΔU - const), получаем

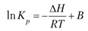
и

где В и В' — некие константы.

Из этих уравнений очевидно, что если тепловой эффект не зависит от температуры, то график зависимости, например, InКр от 1 /Т представляет собой прямую линию. Если известны константы равновесия для нескольких температур, то, построив график в координатах пКр - f(/T), можно определить константу интегрирования и тепловой эффект реакции. Для более точных расчетов нужно учитывать, что тепловой эффект химической реакции тоже зависит от Г.

Если проинтегрировать уравнения (6.6) и (6.7) с учетом граничных температур Т{ и Т2 при постоянных величинах тепловых эффектов, получим выражения, которые можно использовать для оценки Кр (или Кс ) при любых температурах:

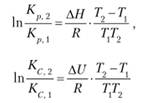
В таких расчетах надо знать ΔН (или ΔU) и значение Кр (или Кс) при одной температуре.