26. Объединенная формула первого и второго начала термодинамики. Свободная энергия Гиббса и Гельмгольца.

G  H – TS	Новая функция, связывающая энтальпию и энтропию – энергия Гиббса
ΔG = (ΔH – TΔS) < 0	Изменение энергии Гиббса при P = const и T = const определяет самопроизвольность процесса
ΔU = Q – Aрасш + E	Если процесс обратимый, то согласно II закону термодинамики: ΔU = TΔS – Aрасш + E

При P = const

E = ΔU +PΔV – TΔS = ΔG

(Объединенная формула первого и второго начала термодинамики)

Величина ΔG характеризует ту часть изменения внутренней энергии, которая может быть превращена в полезную работу.

При V=const

F  U – TS – энергия Гельмгольца.

В изохорном процессе полезная работа определяется изменением энергии Гельмгольца, а условием самопроизвольности процесса является ее уменьшение ΔF < 0

В неизолированных системах процесс протекает самопроизвольно если ему соответствует уменьшение энергии Гиббса. Состояние системы, которому соответствует ΔG = 0 называют состоянием равновесия

• Уравнения Гиббса – Гельмгольца

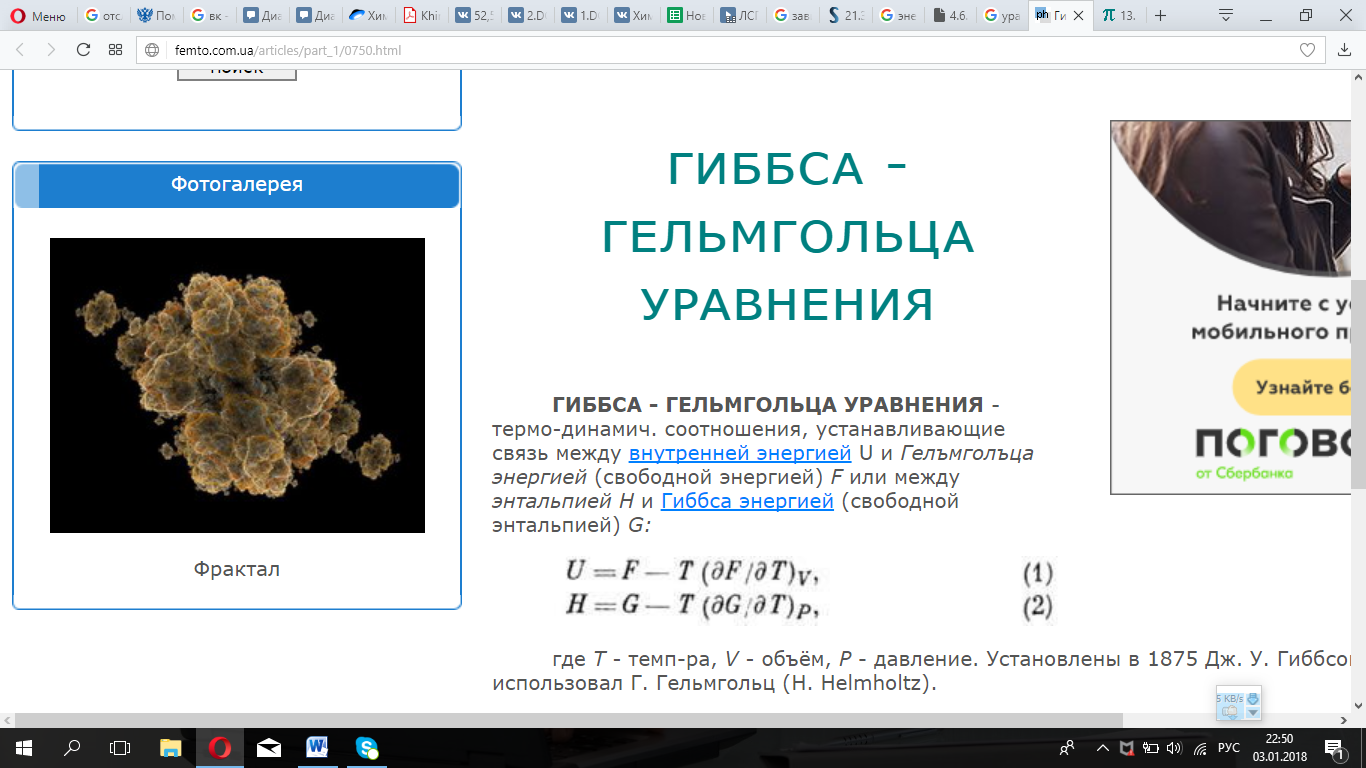
Уравнения Гиббса – Гельмгольца - термодинамические соотношения, устанавливающие связь между внутренней энергией U и Гельмгольца энергией (свободной энергией) F или между энтальпией H и Гиббса энергией (свободной энтальпией) G.

Уравнение (1) следует из определения энергии Гельмгольца F=U-TS и выражения для энтропии .

Уравнение (1) позволяет по энергии Гельмгольца F(T, V) найти внутреннюю энергию U(T, V)и ,следовательно, теплоёмкость при постоянном объёме.

Уравнение (2)-из определения энергии Гиббса G=H-TS и выражения для энтропии .

Уравнениение (2) позволяет по энергии Гиббса G(T, P)найти энтальпию H(T, P)и, следовательно, теплоёмкость при постоянном давлении.

• Энергия Гиббса G

, где ΔН — изменение энтальпии H; ΔS — изменение энтропии S.

Самопроизвольное протекание изобарно-изотермического процесса определяется двумя факторами: энтальпийным, связанным с уменьшением энтальпии системы (ΔH), и энтропийным T ΔS, обусловленным увеличением беспорядка в системе вследствие роста ее энтропии. Разность этих термодинамических факторов является функцией состояния системы, называемой изобарно-изотермическим потенциалом или свободной энергией Гиббса (G, кДж)

Т.к. энергия Гиббса является мерой самопроизвольности протекания процесса, то между знаком ΔG для любой реакции и ее самопроизвольным протеканием (при постоянных температуре и давлении) существуют такие зависимости:

1. Если ΔG отрицательно (ΔG<0), то реакция протекает самопроизвольно в прямом направлении.

2. Если ΔG равно нулю (ΔG=0), то реакция находится в равновесном состоянии.

3. Если ΔG положительно (ΔG>0), то реакция протекать самопроизвольно в прямом направлении не может. Однако обратная реакция идет самопроизвольно.

• Энергия Гельмгольца F

Энергия Гельмгольца системы с определенной внутренней энергией (U), энтропией (S) при абсолютной температуре (Т) определяется уравнением:

F = U – TS

Изменение энергии Гельмгольца для процессов (при постоянных температуре и объеме) можно определить соотношением:

ΔF= ΔU – TΔS

Энергия Гельмгольца подобно энергии Гиббса связана с самопроизвольностью протекания процесса. Если допустить, что система изолирована, а объем и температура постоянны, то самопроизвольно будут протекать только те процессы, при которых F уменьшается.

Таким образом, при ΔF<0 процесс идет самопроизвольно в прямом направлении,

при ΔF>0 – в обратном направлении,

а при ΔF=0 система находится в состоянии равновесия.

Энергию Гельмгольца и энергию Гиббса в стандартных состояниях можно связать с константой равновесия:

ΔG⁰Т = ΔH⁰Т – TΔS⁰Т = —RTlnK,

Где R– универсальная газовая постоянная, K – константа равновесия, Т – абсолютная температура.

Если K>>1, т.е. реакция идет в прямом направлении, то ΔG0˂˂0.

Если K<<1, т.е. реакция идет в обратном направлении, то ΔG0>>0

Если K=1, то ΔG0=0

В случае химической реакции, протекающей в гальваническом элементе при стандартных условиях ΔG⁰ можно связать с ЭДС гальванического элемента следующим соотношением:

ΔG⁰=-nFE⁰, где

nF – количество прошедшего электричества

E⁰ – электродвижущая сила, при условии что все вещества, принимающие участие в реакции, находятся в стандартном состоянии.