1.1.4. Определение токов и напряжений в установившемся режиме постоянного тока

Согласно первому закону Кирхгофа, сумма токов, поступающих в узел, равна сумме токов, уходящих из него. Применительно к данной схеме это выражается следующими уравнениями:

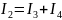
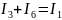
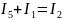
Однако, в данной эквивалентной схеме затруднительно использовать второй закон Кирхгофа, поскольку отсутствуют замкнутые токовые контуры, необходимые для его применения. Поэтому вместо этого прибегаем к закону Ома.

Так как в схеме нет замкнутых путей для прохождения тока, во всех ветвях токи равны нулю:

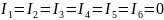
Следовательно, и падения напряжения на резисторах отсутствуют:

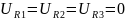
В то же время напряжения на источниках ЭДС остаются равными их номинальным значениям:

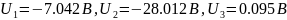
1.2 АНАЛИЗ ЦЕПИ ПРИ ГАРМОНИЧЕСКИХ ФУНКЦИЯХ ИСТОЧНИКОВ ВО ВРЕМЕННОЙ ОБЛАСТИ

1.2.1 Привести схему электрической цепи во временной области

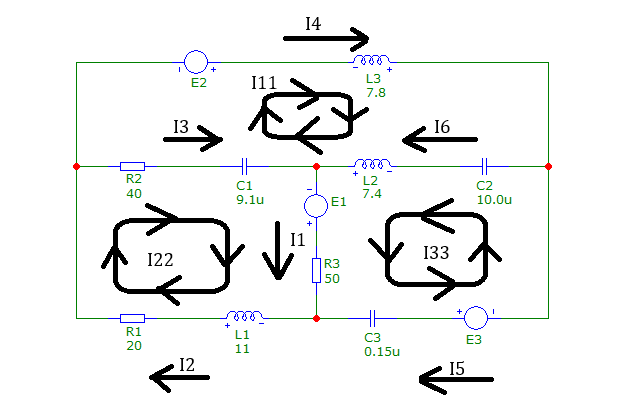
Рис. 5 Схема электрической цепи во временной области

1.2.2 Составить необходимое и достаточное число уравнений цепи, применяя метод уравнений Кирхгофа

По первому закону Кирхгофа:

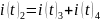
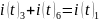
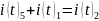
По второму закону Кирхгофа:

Контур 1 (I3-I4-I6):

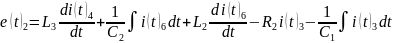
Контур 2 (I3-I1-I2):

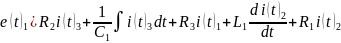
Контур 3 (I1-I6-I5):

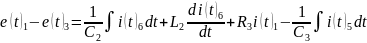
1.2.3 Составить необходимое и достаточное число уравнений, применяя метод контурных токов.

У нас есть 3 контура:

• Верхний: содержит 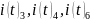, обозначим его как

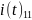
• Левый: содержит 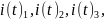обозначим его как

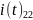
• Правый: содержит 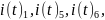обозначим его как

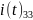
Соотношение токов:

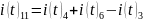
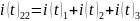
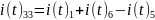
Записываем уравнения для всех контуров:

Контур 1 ( :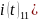

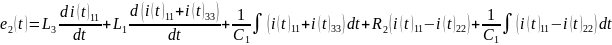
Контур 2 ( ):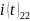

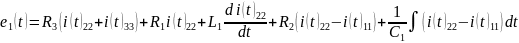
Контур 3 ( ):

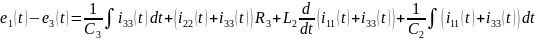
1.2.4 Составить матрицы коэффициентов и правых частей уравнений.

Для составления матриц коэффициентов и правых частей уравнений, необходимо составить систему уравнений по МКТ из п. 1.2.3, а так же сгруппировать элементы в ней:

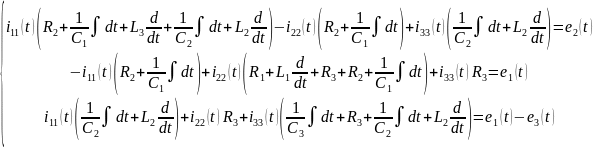
Матрица коэффициентов:

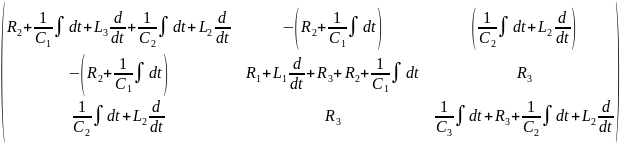
Матрица правых частей уравнения:

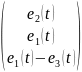
1.2.5. Записать решение для токов в виде матричного соотношения.

=

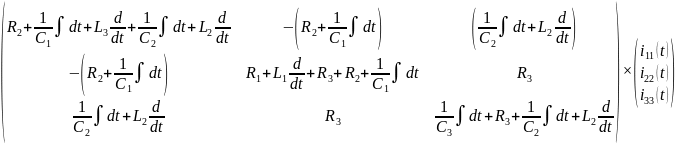1.2.6. Записать и проверить Баланс мощностей.

Формула баланса мощностей для данной схемы имеет вид:

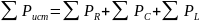
Мощности источников находяться по формуле: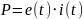

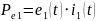
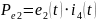
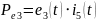Из этого следует, что:

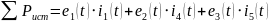
Мощности резисторов находятся по формуле:

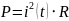
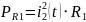
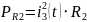
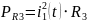Из этого следует, что:

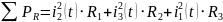
Мощности катушек индуктивности находятся по формуле:

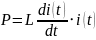
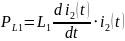
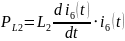
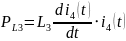Из этого следует, что:

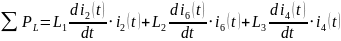
Мощности конденсаторов находятся по формуле:

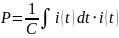
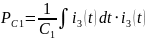
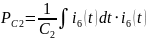
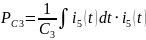Из этого следует, что:

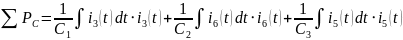
Проверка баланса мощностей:

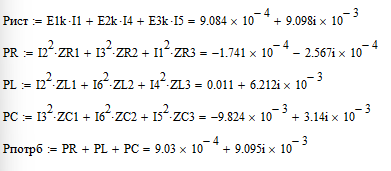
Как можно заметить расхождения находяться в рамках погрешности и не сильно значительны.

1.3. Анализ цепи при гармонических функциях источника в комплексной области

1.3.1. Перевести схему цепи из временной области в комплексную. Привести рисунок схемы в соответствующих обозначениях.

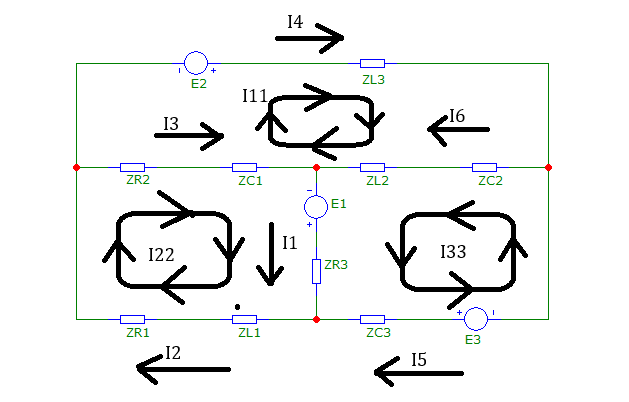
Рис. 6 Схема электрической цепи в комплексной форме

1.3.2. Перевести, полученные матричные уравнения в предыдущем пункте для метода уравнений Кирхгоффа и метода контурных токов, в комплексную форму

Переводим значения резисторов, катушек индуктивности и конденсаторов в комплексную форму:

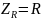
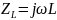
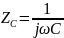
Метод Уравнений Кирхгофа

По первому закону Кирхгофа:

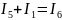
По второму закону Кирхгофа:

Контур 1 (I3-I4-I6):

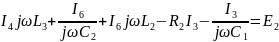
Контур 2 (I3-I1-I2):

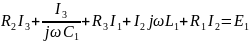
Контур 3 (I1-I2-I5):

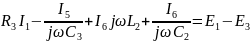
Метод контурных токов:

У нас есть 3 контура:

• Верхний: содержит 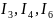, обозначим его как

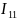
• Левый: содержит 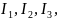обозначим его как

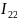
• Правый: содержит 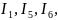обозначим его как

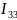
Соотношение токов:

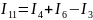
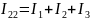
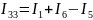
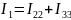
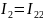
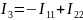
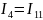
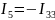
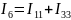
Записываем уравнения для всех контуров:

Контур 1 ( :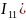

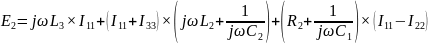
Контур 2 ( ):

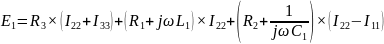
Контур 3 ( ):

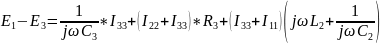
1.3.3. Записать все системы уравнений в матричной форме.

Составим систему уравнений по методу законов Кирхгофа:

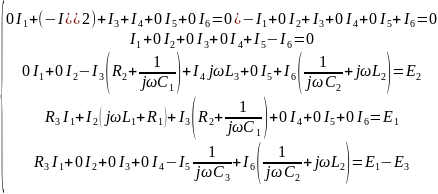
Составим матричное уравнение по методу законов Кирхгофа:

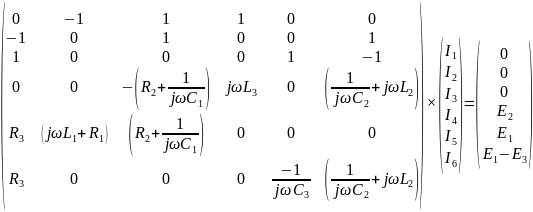
Составим систему уравнений по МКТ:

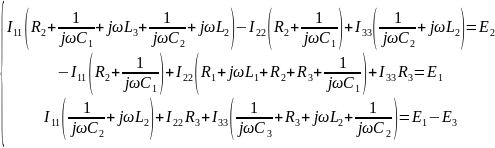
Составим матричное уравнение по МКТ:

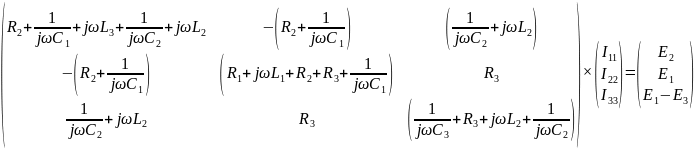
1.3.4. Решить системы уравнений. На основе полученного решения провести полный анализ схемы (определение токов всех ветвей и напряжений на всех элементах).

Перевод значений элементов цепи в комплексную форму:

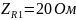
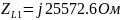
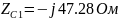
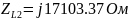
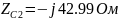
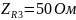
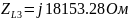
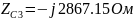
Перевод значений источников ЭДС в комплексную форму:

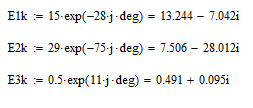
Значение всех ветвеных токов по методу уравений Кирхгофа:

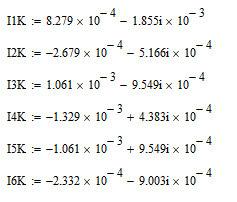
Значение контурных токов:

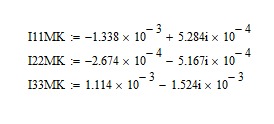
Расчет всех ветвеных токов по МКТ:

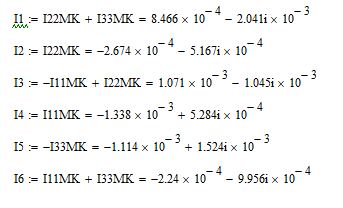
Напряжение на элементах цепи:

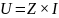
1.3.5. Перевести результаты анализа во временную форму.

Для перевода напряжений и токов из комплексной формы в временную, необходимо воспользоваться формулами:

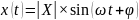
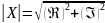
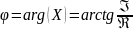
Перевод токов:

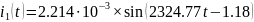
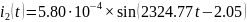
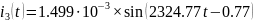
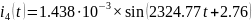
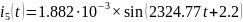
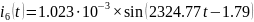
Перевод напряжений:

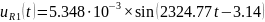
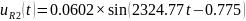
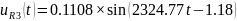
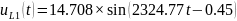
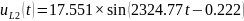
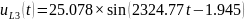
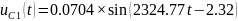
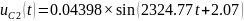
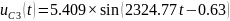
1.4.1. ПРЕОБРАЗОВАТЬ исходную схему электрической цепи

- исключить источники напряжения e1(t), e2(t), e3(t),

- преобразовать в схеме «звезду» в «треугольник».

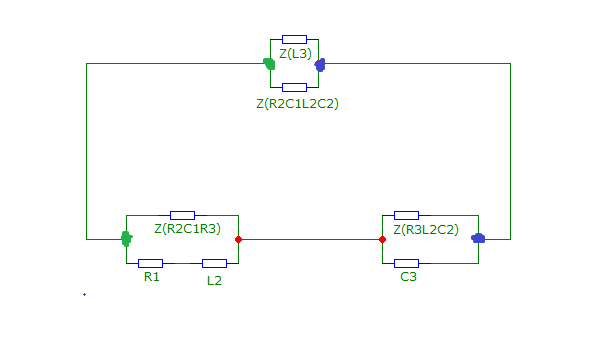
Рис. 7 Преобразованная из «звезды» в «треугольник» схема, с исключенными источниками напряжения

Зеленый цвет – правый узел. Синий цвет – левый узел. Красный цвет – нижний узел.

После предыдущего преобразования можно преобразовать схему в более удобный для расчета четырехполюсник:

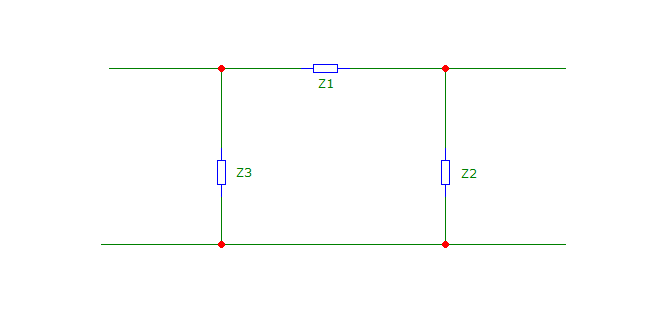
Рис. 8 Схема четырехполюсника

Объяснение преобразований:

После отключения источников напряжения 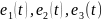, цепь переходит в пассивное состояние, а форма анализа – частотная.

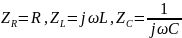
В результате преобразования звезда – треугольник, получена новая схема с трема узлами: левым, правым, нижним. Соответственно образуются три ветви:

• Ветвь 1 – между левым и правым узлами

• Ветвь 2 – между правым и нижним узлами

• Ветвь 3 – между нижним и левым узлами

Каждая ветвь содержит эквивалентные сопротивления, полученные в результате параллельного соединения элементов, оставшихся после преобразования.

Эквивалентное сопротивление для паралельного соединения двух элементов 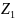и 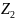определяется по формуле:

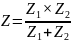
Выражение эквивалентных сопротивлений на ветвях:

Рис. 9 Описание всех преобразований из MathCAD