3. Методические указания

3.1. Внимательно прочитайте текст задания на курсовую работу.

3.2. Выполнение каждого из пунктов задания проводить под соответствующим номером задания.

Каждый из пунктов задания начинается с изображения схемы цепи с необходимыми обозначениями на элементах.

Изображение эквивалентных схем, которые соответствуют принципиальным, должно быть предварительно обосновано с использованием описания условий эквивалентности.

3.3. ОФОРМЛЕНИЕ ПОЯСНИТЕЛЬНОЙ ЗАПИСКИ ПО КУРСОВОЙ РАБОТЕ НАЧИНАЕТСЯ С ТИТУЛЬНОГО ЛИСТА И ПОЛНОГО ТЕКСТА ЗАДАНИЯ НА КУРСОВУЮ РАБОТУ.

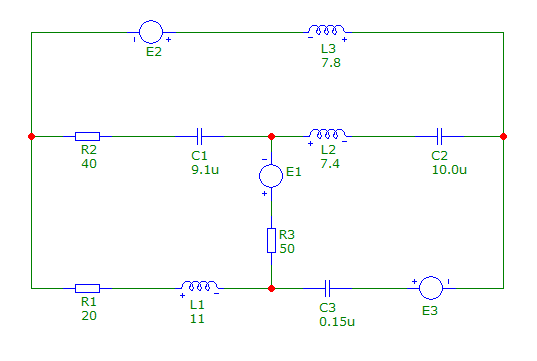
Рис. 1 Принципиальная схема варианта 7

Номер по списку группы — 7. Соответствующая кодовая комбинация — 512346.

Первая цифра 5 означает, что в пятую ветвь последовательно включены R1 и L1. Вторая цифра 1 определяет первую ветвь, в которую включены R2 и C1. Третья цифра 2 указывает на вторую ветвь, содержащую L2 и C2. Четвёртая цифра 3 соответствует третьей ветви, куда последовательно включены источник ЭДС e1(t) и резистивный элемент R3. Пятая цифра 4 указывает на четвёртую ветвь, в которой находятся источник ЭДС e2 и индуктивный элемент L3. Шестая цифра 6 обозначает шестую ветвь, содержащую источник ЭДС e3 и ёмкостный элемент C3.

В соответствии с вариантом 7, номиналы элементов принимаются следующими:

R1 = 20 Ом, R2 = 40 Ом, R3 = 50 Ом

L1 = 11 Гн, L2 = 7.4 Гн, L3 = 7.8 Гн

C1 = 9.1 мкФ, C2 = 10.0 мкФ, C3 = 0.15 мкФ

F = 370 Гц

ЭДС:

e1(t) = 15SIN(ωt - 28) В

e2(t) = 29SIN(ωt - 75) В

e3(t) = 0.5SIN(ωt + 11) В

1.1. Анализ цепи по постоянному току

1.1.1. Получение схемы цепи постоянного тока

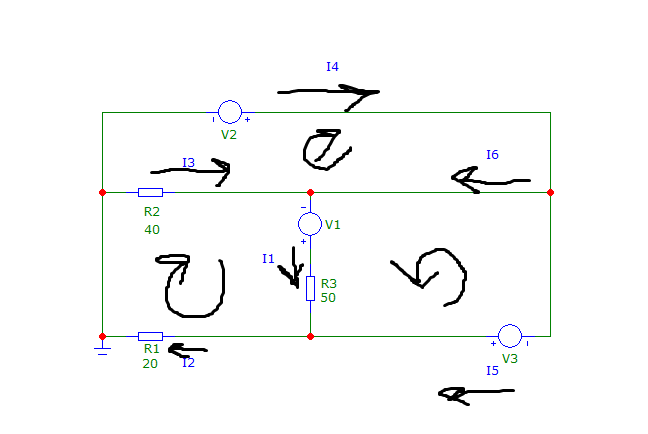
Рис. 2 Эквивалентная схема при ω = 0 в цепи с постоянным током

1.1.2. Эквивалентные источники эдс

Так как по условию мы приравняли частоту к нулю, то источники синусоидального напряжения превращаются в постоянные источники ЭДС. Значения этих ЭДС определяются как средние (постоянные) значения сигналов:

Теперь достаточно узнать значения E1, E2, E3

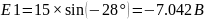
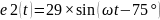
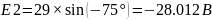
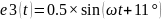
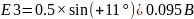
Исходя из этих расчетов мы получаем: E1, E2, E3; которые эквивалентны e1(t), e2(t), e3(t).

1.1.3 Эквивалентные схемы цепи постоянного тока Эквивалентная схема при подключении источников:

При анализе электрических цепей в момент коммутации постоянного тока, когда угловая частота

ω = 0, реактивные элементы заменяются их эквивалентами, отражающими поведение в начальный и установившийся моменты времени.

• В момент времени t = 0:

Индуктивность (катушка) выступает как разомкнутая цепь, поскольку ток через неё не может мгновенно измениться. Это означает, что в начальный момент она препятствует прохождению тока.

Конденсатор в этот же момент эквивалентен короткому замыканию, потому что напряжение на его обкладках не может измениться мгновенно. Он ведёт себя как проводник.

• При t → ∞:

Индуктивность становится эквивалентна обычному проводнику, так как через длительное время её сопротивление постоянному току стремится к нулю.

Конденсатор в установившемся состоянии действует как разрыв цепи, поскольку в постоянном токе он не проводит ток.

Вывод:

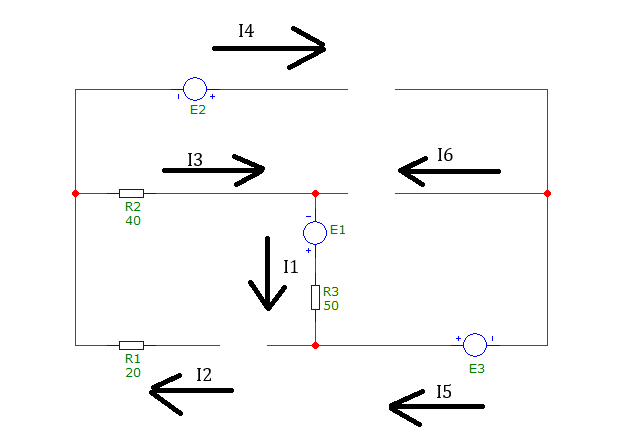
Рис. 3 Схема при t = 0

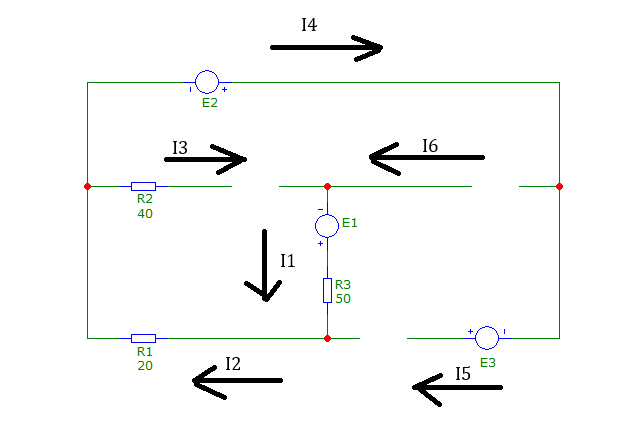
Рис. 4 Схема при t → ∞