Лабы 1-2 / Лабораторная работа #1 Python liberty (1)

Лабораторная работа № 1-2

«Расчет задержек библиотечных элементов с использованием языка высокого уровня Python3»

Краткие теоретические сведения:

Библиотека стандартных ячеек — это коллекция низкоуровневых ячеек для логических функций, триггеров, регистров и буферов. Все ячейки реализованы с фиксированной высотой и переменной шириной. Ключевым свойством библиотек является одинаковость высот ячеек, что позволяет располагать их рядами, упрощая задачу автоматического расположения элементов. Ячейки обычно оптимизированы для уменьшения занимаемой площади и задержки.

Типичная библиотека условно делится на две части:

1. Front-end включает в себя логические описания (Verilog, VHDL), характеризацию ячеек (Synopsys Liberty, ALF и SDF), а также вспомогательные элементы для функциональной верификации (MET, Fastscan и т. д).

2. Back-end содержит описания, относящиеся в физической реализации ячеек. Это физические абстракции в формате Cadence LEF format либо Synopsys Milkyway format, экстрагированные и rtl-нетлисты. В зависимости от условий распространения библиотеки она может содержать дополнительно GDS-файлы, OA- или CDBA-базу данных.

Ядром front-end описания является характеризованная библиотека стандартных элементов. Промышленным форматом де-факто стал Synopsys Liberty Format (.lib), хотя существуют и альтернативные форматы, например, ALF (Advanced library format).

Оригинальный .lib содержит в себе временные характеристики ячеек в табличной форме (NLDM). Обычно используются 2-мерные таблицы, описывающие задержку элемента в зависимости от нагрузки и времени входного фронта.

Пример такой таблицы:

AND cell, cell fall
Input transition, ps	Output capacitance, fF
		0.400	0.798	1.591	3.172	6.325	12.612	25.149	50.148	100.00
	0.4	2.456	2.792	3.371	4.411	6.382	10.252	17.936	33.242	63.758
	3.75	3.184	3.501	4.058	5.091	7.067	10.944	18.633	33.942	64.458
	7.5	3.829	4.149	4.710	5.744	7.717	11.596	19.289	34.600	65.118
	15	4.681	5.038	5.602	6.616	8.595	12.486	20.172	35.487	66.004
	30	5.789	6.194	6.843	7.880	9.821	13.703	21.421	36.713	67.230
	60	7.106	7.582	8.345	9.532	11.502	15.394	23.117	38.448	68.980
	120	8.510	9.079	9.984	11.412	13.624	17.544	25.403	40.864	71.425
	240	9.662	10.328	11.426	13.158	15.875	20.128	28.084	43.972	74.941
	480	9.871	10.658	12.007	14.170	17.550	22.857	31.339	47.510	79.487

Простой поиск по таблице с округлением до ближнего значения может быть визуализирован следующим образом:

AND cell, cell fall, ps Trinp = 15.1 ps; Cout = 12.7 fF
Input transition, ps	Output capacitance, fF
		0.400	0.798	1.591	3.172	6.325	12.612	25.149	50.148	100.00
	0.4	2.456	2.792	3.371	4.411	6.382	10.252	17.936	33.242	63.758
	3.75	3.184	3.501	4.058	5.091	7.067	10.944	18.633	33.942	64.458
	7.5	3.829	4.149	4.710	5.744	7.717	11.596	19.289	34.600	65.118
	15	4.681	5.038	5.602	6.616	8.595	12.486	20.172	35.487	66.004
	30	5.789	6.194	6.843	7.880	9.821	13.703	21.421	36.713	67.230
	60	7.106	7.582	8.345	9.532	11.502	15.394	23.117	38.448	68.980
	120	8.510	9.079	9.984	11.412	13.624	17.544	25.403	40.864	71.425
	240	9.662	10.328	11.426	13.158	15.875	20.128	28.084	43.972	74.941
	480	9.871	10.658	12.007	14.170	17.550	22.857	31.339	47.510	79.487

Билинейная интерполяция

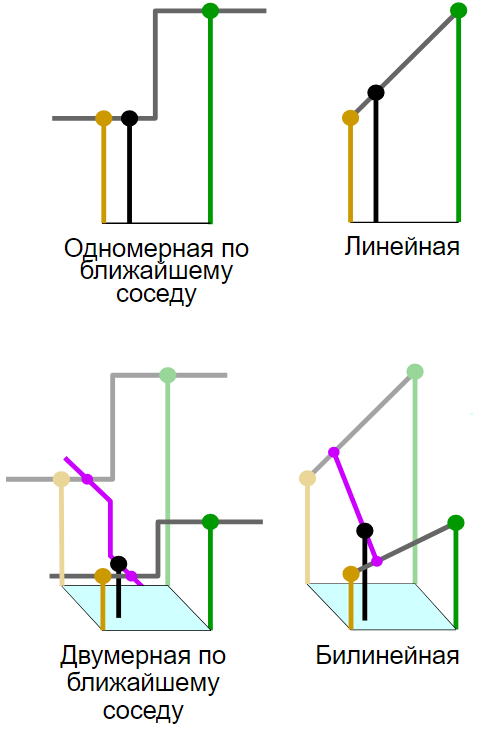
Визуализация использования билинейной интерполяции выглядит так:

AND cell, cell fall, ps Trinp = 15.1 ps; Cout = 12.7 fF
Input transition, ps	Output capacitance, fF
		0.400	0.798	1.591	3.172	6.325	12.612	25.149	50.148	100.00
	0.4	2.456	2.792	3.371	4.411	6.382	10.252	17.936	33.242	63.758
	3.75	3.184	3.501	4.058	5.091	7.067	10.944	18.633	33.942	64.458
	7.5	3.829	4.149	4.710	5.744	7.717	11.596	19.289	34.600	65.118
	15	4.681	5.038	5.602	6.616	8.595	12.486	20.172	35.487	66.004
	30	5.789	6.194	6.843	7.880	9.821	13.703	21.421	36.713	67.230
	60	7.106	7.582	8.345	9.532	11.502	15.394	23.117	38.448	68.980
	120	8.510	9.079	9.984	11.412	13.624	17.544	25.403	40.864	71.425
	240	9.662	10.328	11.426	13.158	15.875	20.128	28.084	43.972	74.941
	480	9.871	10.658	12.007	14.170	17.550	22.857	31.339	47.510	79.487

Дано:

P(y) = 15.1 (ps), P(x) = 12.7 (fF)

Найти: f(P)

Решение:

Согласно таблице, y₁ = 15 ps, y₂ = 30 ps, x₁ = 12.612 fF, x₂ = 25.149 fF.

Отсюда Q₁₁ = 12.486 пс, Q₁₂ = 13.703 пс, Q₂₁ = 20.172 пс, Q₂₂ = 21.421 пс.

f(R₁) = (x₂ - x) / (x₂ - x₁) * Q₁₁ + (x - x₁) / (x₂ - x₁) * Q₂₁ = 12.539 пс.

f(R₂) = (x₂ - x) / (x₂ - x₁) * Q₁₂ + (x - x₁) / (x₂ - x₁) * Q₂₂ = 13.757 пс.

f(P) = (y₂ - y) / (y₂ - y₁) * f(R₁) + (y - y₁) / (y₂ - y₁) * f(R₂) = 12.548 пс.

Для выполнения задания требуется решить ряд задач, основная из которых – парсинг имеющегося файла. Чтение файла осуществляется построчно. Обработку файлов необходимо производить с помощью флагов – отдельно заниматься выставлением флагов, отдельно их обработкой. Флаг – индикатор, который сообщает, что будет находиться на следующих строчках. Например, если текущая строка -- «column_output_capacitance», то на следующей строчке будут находиться индексы для столбцов таблицы NLDM. Необходимо на текущей линии выставить соответствующий флаг, а после перехода на следующую строку и окончания обработки строки флаг сбросить. Некоторые флаги, например, при сохранении таблиц надо держать в течение нескольких строк. Можно искать строки путем строгого сравнения с заданным шаблоном, что неудобно, поскольку приходится учитывать все пробелы в конце и начале строки и символы перехода на новую строку. Можно воспользоваться функцией match из библиотеки регулярных выражений re, которая будет проверять наличие заданного шаблона в строке и возвращать единицу в случае, если такой шаблон в строке присутствует.

После обнаружения нужных строк необходимо обработать – после сохранения строк это всё ещё строки, которые надо преобразовать в массив из чисел. Во-первых, необходимо удалить символы перехода на новую строку с помощью метода replace(), заменяя символ “\n” на пустую строку. Во-вторых, необходимо «разбить» строку на составляющие с помощью функции split(), указав в качестве разделителя запятую. В-третьих, необходимо изменить тип данных полученного массива со строковых на численные с форматом плавающей запятой. Это можно сделать разными способами. Можно через цикл преобразовать каждый элемент к типу данных float и оставить тот же list. Можно воспользоваться функцией создания массива array из библиотеки математических функций numpy и получить массив numpy, можно воспользоваться list comprehension и получить новый list.

После парсинга всех требуемых значений необходимо воспользоваться приведенными выше формулами для получения результата билинейной интерполяции.

Примеры с кодом приведены здесь https://replit.com/@elkapetan/VIaPIV-Laboratornaia-rabota-1-2

Задание на лабораторные работы 1-2:

1. Написать скрипт, рассчитывающий выходную задержку и время выходного фронта в зависимости от нагрузки и времени входного фронта в соответствии с вариантом. В случае, если значение выходной емкости и времени входного фронта не совпадают с индексными значениями, округлить их до ближайшего индексного значения.

Вариант 1	Вариант 2	Вариант 3	Вариант 4	Вариант 5
AND, p	NAND, p	BUF, p	INV, p	OR, p
Вариант 6	Вариант 7	Вариант 8	Вариант 9	Вариант 10
NOR, p	XOR, p	XNOR, p	AND, n	NAND, n
Вариант 11	Вариант 12	Вариант 13	Вариант 14	Вариант 15
BUF, n	INV, n	OR, n	NOR, n	XOR, n
Вариант 16	Вариант 17	Вариант 18	Вариант 19	Вариант 20
XNOR, n	AND, p	NAND, p	BUF, p	INV, p

2. Добавить в существующий скрипт расчет с использованием билинейной интерполяции.

3. Переписать код, оформив класс Gate с методами get_delay(edge, tr_in, c_out), get_transition(edge, tr_in, c_out), propagate(edge, tr_in, c_out).

4. Использовать код для расчета схемы из нескольких элементов в соответствии с вариантом. Второй вход для логических элементов выбирать таким образом, чтобы обеспечить переключение элемента.

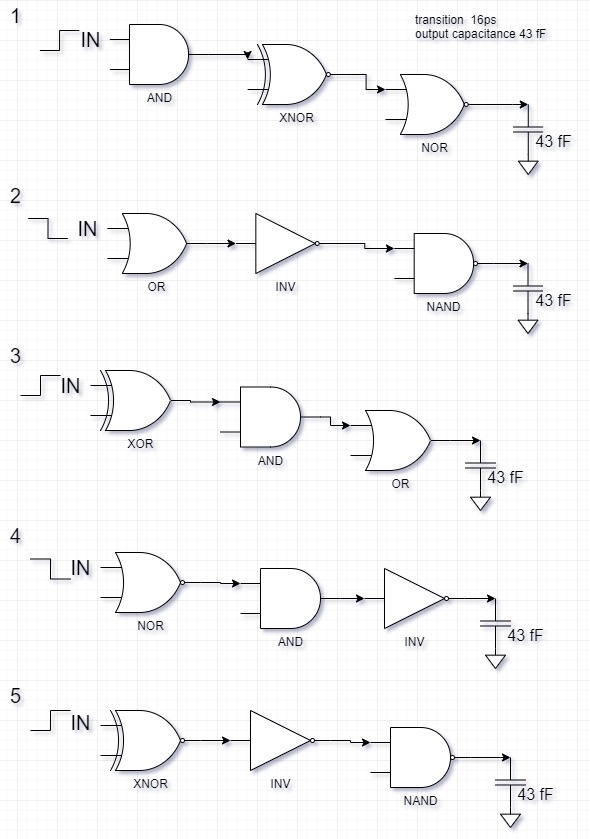
Вариант 1, 6, 11, 16 – схема #1;

Вариант 2, 7, 12, 17 – схема #2;

Вариант 3, 8, 13, 18 – схема #3;

Вариант 4, 9, 14, 19 – схема #4;

Вариант 5, 10, 15, 20 – схема #5.

5. Оформить в формате Word отчет о выполненной работе. Требования к отчету:

• название работы / формулировка заданий;

• таблица истинности для каждой схемы;

• заключение по результатам выполненной работы.