ОТЧЕТ_НИР_1_СЕМ

МИНОБРНАУКИ РОССИИ САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ ЭЛЕКТРОТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

«ЛЭТИ» ИМ. В.И. УЛЬЯНОВА (ЛЕНИНА)

Кафедра САУ

ОТЧЕТ по учебной практике

Тема: Классификация алгоритмов фазовой автоподстройки частоты

Санкт-Петербург

2023

ЗАДАНИЕ

НА НАУЧНО-ИССЛЕДОВАТЕЛЬСКУЮ РАБОТУ

Студент: Плотников Д.А.

Группа: 9492

Тема НИР: Классификация алгоритмов фазовой автоподстройки частоты

Задание на НИР:

Форма отчетности: Пояснительная записка (объем ≥ 15 с).

Сроки выполнения НИР: 25.09.2023 – 15.12.2023

Дата сдачи отчета:

Дата защиты отчета:

2

АННОТАЦИЯ

Целью работы является ознакомление и изучение темы алгоритмов фазовой автоподстройки частоты, их классификации, а также исследование средствами математического моделирования алгоритмов фазовой автоподстройки частоты в однофазной системе (непрерывная и дискретная реализация).

SUMMARY

The purpose of this work is to familiarize and study the topic of algorithms of phase frequency autotuning, their classification, as well as research by means of mathematical modeling algorithms of phase frequency autotuning in a single-phase system (continuous and discrete implementation) and the formulation of the purpose and objectives of the graduate qualification work.

3

4

полупроводниковых силовых устройств, таких как импульсные источники питания или регуляторы частоты вращения электродвигателей. Для устранения высших гармоник тока применяют параллельный активный силовой фильтр

(АСФ). В таких системах синхронизация играет критическую роль, поскольку ошибки в синхронизации могут существенно снизить эффективность работы системы или привести к аварии. В работе [2] предлагается решение данных проблем с использованием блока синхронизации, использующего ФАПЧ и базирующегося на математических преобразованиях, таких как последовательные преобразования Э. Кларка и Парка-Горева в синхронную вращающуюся систему координат.

6

1. КЛАССИФИКАЦИЯ АЛГОРИТМОВ ФАПЧ

Принципиальная схема системы ФАПЧ, состоящая из трех частей, показана на рисунке 1.1. Она включает в себя фазовый детектор (ФД), фильтр нижних частот (ФНЧ) и генератор, управляемый напряжением (ГУН).

Рисунок 1.1 — Принципиальная схема ФАПЧ

Первый блок генерирует выходной сигнал пропорционально разности фаз между входным сигналом – v и выходным сигналом генерируемым ГУН – v’.

ФНЧ представляет собой блок, который фильтрует низкие частоты для ослабления высокочастотных составляющих сигнала на выходе ФД. ГУН формирует на выходе сигнал, частота которого сдвинута относительно заданной центральной частоты в зависимости от входного напряжения, подаваемого ФНЧ.

1.1. Стандартный алгоритм ФАПЧ

На рисунке 1.2 представлена схема простейшего алгоритма ФАПЧ,

используется если входной сигнал не имеет гармонических искажений.

Рисунок 1.2 — Схема простейшего ФАПЧ

В данном алгоритме в качестве ФД используется оператор умножения,

который перемножает входной сигнал с сигналом обратной связи. Как показано

7

на схеме, сигнал обратной связи – косинусоида, это означает, что если входной сигнал был задан в виде синусоиды, то возникнут высокочастотные и низкочастотные составляющие сигнала. В качестве ФНЧ используется ПИ-

регулятор, который помимо фильтрования имеет свойство регулирования динамической характеристики. Данный алгоритм способен достаточно быстро и точно определять частоту и фазу входного сигнала (только тогда, когда отсутствуют какие-либо гармонические искажения входного сигнала). Главным недостатком алгоритма является колебание двойной частоты. Полученная частота на выходе ФАПЧ будет изменяться по гармоническому закону,

амплитуда которого определяется по формуле:

2

2 = , (1.1)

20

где ωn – это частота собственных колебаний линеаризованного контура, можно принять равной ωn ≈ 0,1ω0.

1.2. ФАПЧ на основе генератора ортогональных сигналов

С целью обеспечения высокого качества электроэнергии в параллельно работающих сетях для управления фазой и частотой требуется быстрая и надежная система. Для этого используется алгоритм ФАПЧ с генератором ортогональных сигналов (ОСГ), который может подавлять гармоники и смещение постоянной составляющей. Такая система состоит из трех основных частей: ФД, включающий в себя ОСГ и блок опорного преобразователя, ГУН и ФНЧ, устанавливаемый между фазовым детектором и ГУН [3]. Здесь в качестве ФНЧ применяется ПИ-регулятор (см. рисунок 1.3).

8

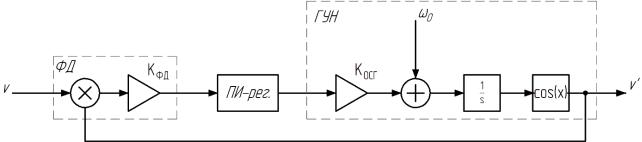
Рисунок 1.3 — Структурная схема простейшей ФАПЧ В качестве блока ОСГ в данной схеме можно рассматривать способ с

задержкой при передаче сигнала и блок, использующий преобразование Гилберта [4]. Основным различием первого способа является то, что все гармоники входного сигнала подвергаются одинаковой временной задержке.

При использовании метода преобразования Гилберта все гармоники сдвигаются по фазе на 90 град. Согласно [5], второй способ сложнее и хуже по сравнению с блоком с задержкой по времени. Способ с блоком задержки легко реализуется за счет использования буфера, работающего по принципу "первый пришел - первый ушел" (FIFO), размер которого составляет одну четвертую от количества выборок, содержащихся в одном цикле основной частоты. Но данный способ имеет два недостатка: блок зависит от частоты из-за фиксированной задержки,

поэтому могут возникнуть проблемы при колебаниях частоты сети, и создает нефильтрованную ортогональную систему.

1.3. ФАПЧ с преобразованием Парка

Структурная схема данной системы представлена на рисунке 1.4. В данном алгоритме ФАПЧ отсутствует блок ГУН, вместо него с целью определения фазового угла для синусоидальных функций преобразования Парка, добавлен генератор частоты/фазового угла (“frequency/phase-angle generator” FPG) [6].

9