
пример_курсач_гаврилов
.pdf
Рисунок 8 - Программируемые интеллектуальные реле Siemens LOGO
В данном дипломном проекте при разработке систем защиты ис-
пользовался программируемый микроконтроллер Siemens LOGO.
21
2. Имитационное моделирование систем защитыэлектроприводов
переменного тока
На сегодняшний день почти все процессы и методы сначала моделируются, до их фактической реализации. Это значительно снижает количество попыток и затраты на фактическую реализацию. Эксплуатационные характеристики системы можно точно оценить с помощью соответствующих имитационных моделей. Таким образом, модели должны быть гибкими и точ-
ными, а также учитывать проблемы фактической реализации. В данный момент благодаря стремительному развитию аппаратного и программного обеспечения доступны новые более быстрые и удобные для использования пакеты программ для моделирования.
2.1Расчет параметров схемы замещения асинхронногодвигателя
В справочной литературе отсутствуют параметры схемы замещения элек-
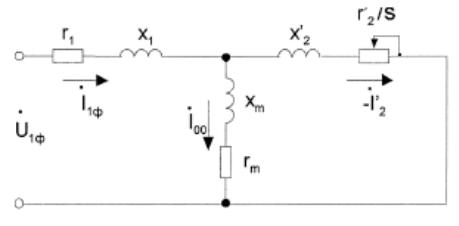
тродвигателя. Для определения параметров воспользуемся наиболее простой и удобной Т-образной схемой замещения, представленной на рисунке 9. [7]
Рисунок 9 - Т-образная схема замещения
Исходными данными являются каталожные данные асинхронного двига-
теля АИР56А4У3, представленные в таблице 1.
22

Таблица 1 – Каталожные данные асинхронного двигателя АИР56А4У3
|
Рн, кВт |
Uн, В |
nном, |
nмакс, |
ηном |
cosφн |
ki |
km |
J, кг/м2 |
|
об/мин |
об/мин |
|||||||
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
0,12 |
220 |
1350 |
1500 |
0,57 |
0,66 |
5 |
2,2 |
0,0007 |
|
|
|
|
|
|
|
|
|
|
где Рн – номинальная мощность двигателя; |
|
|
|
|
|||||
|
Uн – номинальное напряжение; |
|
|
|
|
|
|||
|
nном |
– номинальная частота вращения; |
|
|
|
|
|||
|
nmax |
– максимальная частота вращения; |
|
|
|
|
|||
|
ηном |
– коэффициент полезного действия; |
|
|
|
|
|||
cosφн – коэффициент мощности; ki – кратность пускового тока;
kп – кратность пускового момента;
J – момент инерции двигателя.
Расшифровка маркировки электродвигателя АИР56А4:
А – асинхронный И – двигатель унифицированной серии по стандарту «Интерэлектро»
Р (или С) – привязка мощности к установочно-присоединительным раз-
мерам согласно стандарту РС3031-71; С: CENELEC.
56 - один из габаритов электродвигателя АИР 56А4 – высота оси
вращения в мм, от центра вала до основания лап электродвигателя.
А - длина сердечника статора.
4 - в электродвигателе АИР 56А4 – четыре полюса, которые соответ-
ствует частоте вращения 1500 об/мин.
Ток холостого хода асинхронного двигателя можно найти по следующему
выражению:
|
|
|
2 |
|
|
p* I1Н (1- sН ) 2 |
|
|
|
|
2 |
|
0, 75 0, 394 (1- 0,1) 2 |
|
|
|
||||||||
|
|
I |
11 |
-[ |
|
|
|
|
|
] |
|
|
|
0, 435 |
|
-[ |
|
|
|
] |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(1- 0, 75 0,1) |
|
|
|
|||||||||
|
|
|
|
|
(1- p*sН ) |
|
|
|
|
|
|
|
|
|
|
|
||||||||
I0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
0, 449 А, |
(1) |
|||||||||
|
|
|
|
|
p* (1- sН ) |
2 |
|
|
|
|
|
|
0, 75 (1- 0,1) |
2 |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
1-[ |
|
|
|
] |
|
|
|
|
|
1-[ |
|
] |
|
|
|
|
||||
|
|
|
|
(1- p s |
Н |
) |
|
|
|
|
|
(1- 0, 75 0,1) |
|
|
|
|
||||||||
|
|
|
|
|
|
|
* |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
23
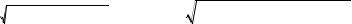
где Sн - номинальное скольжение;
|
|
|
|
|
sн 0 |
- н |
157,08 -141,37 |
|
0,1, |
(2) |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
157,08 |
|
|
|
|
|
|
|||
где ω0 - скорость холостого хода, рад/с; |
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
0 |
2 nmax |
|
2 1500 |
157,08 рад / с; |
(3) |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
60 |
|
|
|
|
|
60 |
|
|
|
|
|
|
|
|
|||||||
ω н - номинальная скорость вращения, рад/с; |
|
|
|
|
|
||||||||||||||||||||||
|
ном |
|
2 nном |
|
2 1350 |
141,3 рад / с; |
(4) |
||||||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
60 |
|
|
|
|
|
60 |
|
|
|
|
|
|
|
|
|||||||
I1н - номинальный ток статора двигателя; |
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
P |
|
|
|
|
|
|
|
|
|
|
|
|
120 |
|
|
|
|
|
|
|
I |
|
|
|
|
|
|
н |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0, 483 А. |
(5) |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
3 U |
|
|
cos |
Н |
|
|
|
220 |
0, 66 |
|
|
|
|||||||||||||||
1н |
|
н |
3 |
0, 57 |
|
|
|||||||||||||||||||||
|
|
|
|
|
н |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
I11 - ток статора двигателя при частичной загрузке; |
|
||||||||||||||||||||||||||
I11 |
|
|
|
|
pж PН |
|
|
|
|
|
|
|
|
|
0, 75 120 |
|
0, 468 А. |
(6) |
|||||||||
3 U1Н |
|
cos fp |
ж |
p |
ж |
|
|
3 220 0,55 |
0,53 |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Коэффициент загрузки двигателя |
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
pж |
P |
0, 75 |
|
|
|
|
(7) |
|||||||||||
|
|
|
|
|
|
|
|
|
Pн |
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Из формулы Клосса определяем соотношение, которое необходимо для расчета критического скольжения:
|
|
|
|
|
|
|
0,1 |
2, 2 |
2, 22 -[1- 2 0,1 1 (2, 2 -1)] |
0,577. |
|
s |
s |
|
|
km |
km2 -[1-2 sН (km -1)] |
(8) |
|||||
Н |
|
|
|
|
|
||||||
к |
|
|
1- 2 sН (km -1) |
|
|
|
1- 2 1 (2, 2 -1) |
|
|||
|
|
|
|
|
|
|
|
||||
значение коэффициента находится в диапазоне 0,6 – 2,5, поэтому в пер-
вом приближении принимаем =1,25.
С1 |
1 ( |
|
I |
0 |
) 1 |
|
0, 449 |
1, 093. |
(9) |
|
ki |
I1Н |
2 5 0, 492 |
||||||
|
2 |
|
|
|
|
||||
Активное сопротивление ротора, приведенное к обмотке статора асинхронного двигателя
R' |
|
|
3 U 2 |
(1- s ) |
|
|
|
3 220 (1- 0,1) |
69, 465Ом. |
|
||||
|
|
|
н |
Н |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
||||
2 |
|
|
|
|
|
|
1 |
|
|
|
1 |
|
|
(10) |
|
|
2 C |
2 k |
|
P ( |
) |
|
2 1, 0932 2, 2 120 (1, 25 |
) |
|
||||
|
m |
|
|
|
||||||||||
|
1 |
|
|
Н |
sК |
0,1 |
|
|
||||||
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
24 |

Активное сопротивление статорной обмотки можно определить по следу-
ющему выражению
R1 C1 R2' |
1, 092 69, 465 1 94,907 Ом. |
(11) |
|||||||||
Определим параметр , который позволит найти индуктивное сопротив- |
|||||||||||
ление короткого замыкания Хкн: |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
- |
2 |
|
1 |
|
2 |
1,199. |
(12) |
||
|
|
|
|
|
-1, 25 |
|
|||||
2 |
|
|
2 |
||||||||
|
sk |
|
|
|
|
0,577 |
|
|
|
|
|
Тогда |
|
|
|
|
|
|
|
|
|
|
|
XКH С1 |
R2' 1,199 1, 089 69, 465 91, 069Ом. |
(13) |
|||||||||
Для того чтобы выделить из индуктивного сопротивления Хкн сопротив-
ления рассеяния фаз статора и ротора, необходимо воспользоваться соотноше-
ниями, которые справедливы для серийных асинхронных двигателей.
Индуктивное сопротивление роторной обмотки, приведенное к статор-
ной, может быть рассчитано
X 2' |
0, 58 X KH |
|
0, 58 91, 069 |
48, 326 Ом. |
(14) |
C1 |
|
||||
|
1, 093 |
|
|
||
Индуктивное сопротивление статорной обмотки может быть определено |
|||||
по следующему выражению |
|
|
|
|
|
X1 0, 42 Xкн |
0, 42 91,389 38, 249Ом. |
(15) |
|||
Согласно векторной диаграмме ЭДС ветви намагничивания E1 ,
наведенная потоком воздушного зазора в обмотке статора в номинальном ре-
жиме, равна
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
E |
(U |
1Н |
cos f |
- R I |
Н |
)2 (U |
1Н |
sin f |
X |
1Н |
I |
Н |
)2 |
|
||||||
1 |
|
|
1Н |
1 |
|
|
|
1Н |
|
|
|
|
(16) |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
220 0, 66 - 94,907 0, 492 2 220 0, 75 - 38, 249 0, 492 2 |
||||||||||||||||||||
177, 242 В. |
||||||||||||||||||||
Тогда индуктивное сопротивление намагничивания |
|
|||||||||||||||||||
|
|
|
|
|
Xμ |
|
E1 |
|
177, 242 |
394,317 Ом. |
(17) |
|||||||||
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
I0 |
|
|
0, 449 |
|
|
|
|
|
|
|
||
25
Исходя из расчетов индуктивных сопротивлений, рассчитаем индуктив-
ность обмотки статора, ротора, намагничивания, по формуле
L1 |
|
|
|
X1σ |
|
|
|
|
38, 249 |
|
|
0,122 Гн; |
(18) |
|||
2 |
|
|
|
|
2 50 |
|
|
|||||||||
|
f1 |
|
|
|
|
|||||||||||
L2 |
|
|
X 2' |
σ |
|
|
|
|
|
48,326 |
|
|
0,154Гн; |
(19) |
||
|
|
|
|
|
|
|
|
2 50 |
|
|
||||||
|
2 |
f1 |
|
|
|
|
|
|||||||||
L |
|
|
X |
μ |
|
|
|
|
|
394, 314 |
|
|
1, 255Гн. |
(20) |
||
|
|
|
|
|
|
|
|
|
|
|
||||||
2 |
|
|
|
|
2 50 |
|
|
|||||||||
|
|
|
f1 |
|
|
|
|
|
||||||||
2.2Расчет статических характеристик
Используя параметры схемы замещения, рассчитаем естественные механические и электромеханические характеристики.
Расчет естественной механической характеристики проводим по выраже-
нию (21).
M (s) |
|
|
|
|
2 U 2 |
R ' |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
н |
|
2 |
|
|
|
|
|
|
|
, |
|
||
|
|
|
2 |
|
|
|
R ' |
|
2 |
|
R R |
' |
|
2 |
|
(21) |
||
|
0 |
s X |
|
|
(R1 |
|
|
2 |
) |
|
( |
1 2 |
|
) |
|
|
|
|
кн |
|
|
s |
|
s Xμ |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рисунок 10 - Естественная механическая характеристика АД
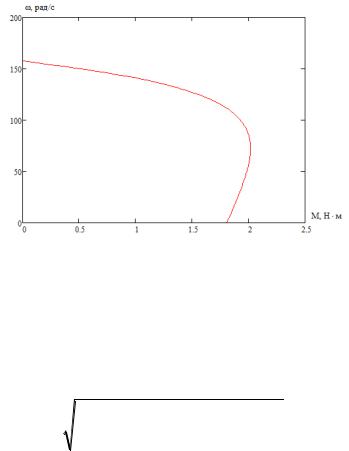
Естественные электромеханические характеристики I1 s и |
|
s элек- |
|||||||||||||||
I2 |
|||||||||||||||||
тродвигателя рассчитывается для частоты |
f1н 50 Гц по выражению (22). |
||||||||||||||||
I ' (s) |
|
|
|
Uн |
2 |
|
|
|
|
|
|
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
2 |
|
|
|
|
R |
' |
|
|
|
R R |
' |
|
|
|
|
|
(22) |
|
|
|
2 |
(R |
|
2 |
( |
|
2 |
|
|
|
|||||
|
|
X |
|
2 |
|
) |
|
1 2 |
|
) |
|
|
|
|
|
||
кн |
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
1 |
s |
|
|
|
|
s X |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
26 |
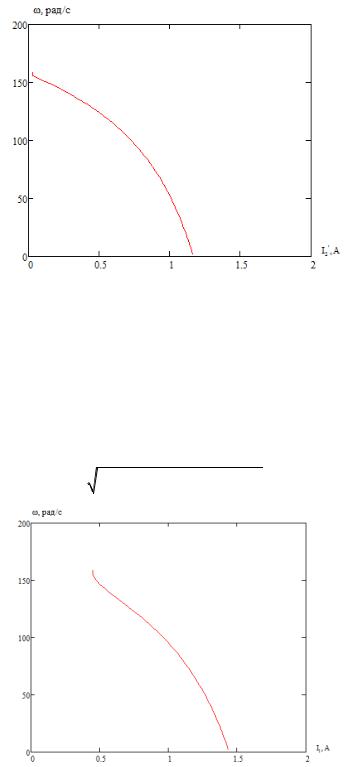
Рисунок 11 - Естественная электромеханическая характеристика АД ротора
Полагая, что ток намагничивания двигателя имеет полностью реактивный характер, выражение для электромеханической характеристики, описывающей зависимость тока статора от скольжения, запишется следующим образом
|
|
s = |
|
|
|
|
|
|
|
|
I |
1 |
I |
2+I' |
(s)2+2 I |
0 |
I' |
sinφ (s), |
(23) |
||
|
|
0 |
2 |
|
2 |
2 |
|
|
||
Рисунок 12 - Естественная электромеханическая характеристика АД статора
2.3Математическое описание модели асинхронногодвигателя
При построении реальных систем электропривода переменного тока в
системы управления включают преобразователи фаз 3/2 и 2/3. [8].
27

Первый (3/2) –осуществляет преобразование трехфазных напряжений UA, UB, UC (формула) в двухфазные Uα, Uβ, в соответствии с выражениями (24, 25)
|
|
U A Um sin t, |
|
|
|
|
|
||||||
|
|
U |
|
U |
|
|
sin( t |
|
2 |
), |
|
||
|
|
B |
|
m |
3 |
((24) |
|||||||
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
U |
|
U |
|
sin( t |
2 |
). |
|
||||
|
|
C |
m |
|
|
||||||||
|
|
|
|
|
|
|
3 |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
||
US |
|
2 |
U |
2 |
(U A aUB a2UC ), |
|
|||||||
3 |
3 |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
a e j |
|
1 |
|
j |
|
3 |
|
|
|
|
||||
3 |
|
|
, |
|
((25) |
|||||||||
2 |
|
|
|
|
||||||||||
|
|
|
|
|
|
2 |
|
|
|
|
||||
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
a2 e j |
|
|
1 |
|
|
|
|
3 |
. |
|
||||
3 |
j |
|
|
|
||||||||||
|
|
|
|
|
||||||||||
|
|
|
|
|
|
2 |
|
|
2 |
|
|
|||
где а – оператор поворота;
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
US |
U jU |
2 |
(U A aUB a2UC ) |
2 |
(U A |
( |
1 |
j |
|
3 |
)UB |
( |
1 |
j |
3 |
)UC ). (26) |
|
3 |
3 |
2 |
|
|
2 |
|
|||||||||||
|
|
|
|
|
|
2 |
|
|
|
2 |
|
||||||
После преобразования уравнения (26) получим
U 2[U A (UB UC ) / 2] / 3,
U (UB UC ) /  3.
3.
((27)
28
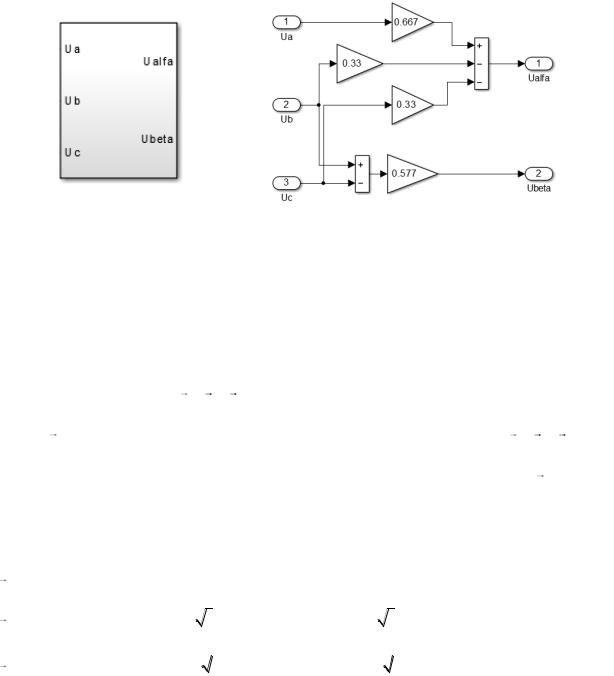
а)
б)
Рисунок 13 – Преобразователь (3/2):
а) условное графическое обозначение преобразователя;
б) модель преобразователя в Simulink
При разработке преобразователя (2/3) следует иметь в виду, что фазный
вектор трехфазной системы U A ,UB ,UC представляет проекцию пространствен-
ного вектора U S на оси А, В, С. Выражения для фазных напряжений U A ,UB ,UC
представляют действительную часть проекции пространственного вектора U S на фазные оси А, В, С.
В соответствии с этим, имеем следующую систему выражений:
U A |
Re(US ) Re(U jU ) Ua , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
U |
|
Re(a Ua ) Re[( |
1 |
j |
|
|
3 |
)(U |
|
jU |
|
) |
1 |
U |
|
j |
|
3 |
U , |
|
||||||||||||||||
|
2 |
|
2 |
|
|
2 |
|
|
|
|
((28) |
|||||||||||||||||||||||||
|
B |
|
S |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
2 |
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
U |
|
Re(a |
Ua |
|
) Re[( |
1 |
j |
|
3 |
)(U |
|
jU |
|
) |
1 |
U |
|
j |
|
|
3 |
U |
|
, |
||||||||||||
C |
S |
|
|
|
|
|
|
a |
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
2 |
|
|
2 |
|
|
|
|
|
2 |
|
|
|
|
2 |
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
29

а) |
б) |
|
|
|
Рисунок 14– Преобразователь (3/2): |
а) условное графическое обозначение преобразователя;
б) модель преобразователя в Simulink
Для исследования в среде Matlab используем двухфазную модель реаль-
ной трёхфазной машины в системе координат α, β. Такая замена переменных ши-
роко используется при математическом исследовании электрических машин с целью упрощения систем дифференциальных уравнений электрического равновесия статорных и роторных цепей.
Обобщенная система уравнений для описания асинхронной двигателя с короткозамкнутым ротором имеет вид:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
S |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d |
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
us Rs is |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
dt |
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
0 R |
|
|
|
|
|
d |
R |
|
|
|
|
|
|||||||||||||||||||||||||||
i |
|
||||||||||||||||||||||||||||||||||||||
|
|
jp |
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
R R |
|
|
|
|
|
dt |
|
|
|
|
|
|
R |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
S |
x i |
|
x |
i |
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
s s |
|
|
|
|
|
m R |
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(29) |
||
|
|
R |
x i |
|
|
x |
|
|
|
i |
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
R R |
|
|
|
|
|
|
|
m s |
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
M |
e |
|
pk |
( |
|
|
|
i ) |
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i k |
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
d |
|
|
M e |
M c |
|
||||||||||||||||||||||||||||||
J |
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
dt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
Подставив уравнения потокосцеплений в уравнения напряжений полу-
чим:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R |
|
x |
|
dis |
|
x |
diRs |
|
(30) |
||
|
|
|
i |
|||||||||||
u |
|
|||||||||||||
|
|
|
|
|
|
|
|
|||||||
|
|
s |
s s |
s dt |
|
m dt |
|
|
||||||
30
