Билет №13

Билет № 13. Студент гр. ХХХХ ХХХХХХХХХХХ

Вопрос 1.

4.7 Теорема 3.4 об условиях достижения цели управления, заданной при помощи интегрального целевого функционала алгоритмом скоростного градиента в дифференциальной форме вида (3.14) (или (3.38)).

Модель управляемого объекта в виде дифференциальных уравнений состояния соответствует выражению

(3.26)

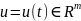где – вектор состояния, – вектор входов системы.

Рассматривается случай, когда цель управления задана при помощи интегрального целевого функционала

и соответствующего алгоритма скоростного градиента в дифференциальной форме вида

(3.38)

Следующая теорема устанавливает условия достижения указанной цели в системе с алгоритмом (3.38).

Теорема 2.4. Рассматривается система (3.26), (3.38) при следующих предположениях:

1. Функции непрерывна по , , кусочно-непрерывны по и локально ограничены равномерно по .

2. Для всех величины неотрицательны.

3. Функция выпукла по .

4. Существуют постоянный вектор и скалярная функция со свойствами

такие, что для любого решения системы (3.26) при выполняется неравенство

Тогда:

1) достигается цель управления , где

2) любое ограниченное решение системы (3.26), (3.38) удовлетворяет соотношению

Вопрос 2.

11.2 Применение (вместо робастного адаптивного управления высокого порядка (по теореме 6.12), тема 9) из вопроса 45) нелинейного робастного алгоритма высокого порядка (по теореме 6.13, тема 9) для объекта с возмущением (теорема 6.19). Пример 6.7.

Класс линейных стационарных объектов описывается уравнением вида

(6.343)

где и – регулируемая переменная и сигнал управления соответственно, – внешнее ограниченное возмущение, и – нормированные полиномы с неизвестными коэффициентами такие, что

Желаемое поведение регулируемой переменной у с помощью эталонной модели определяется как

(6.344)

где – эталонный выход, – сигнал задания, – нормированный гурвицев полином степени , 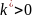– постоянный коэффициент.

Вместе с моделью объекта управления рассматриваются вспомогательные фильтры вида

	(6.203)
	(6.204)

Настраиваемый регулятор выбирается в стандартном виде

(6.353)

Динамический порядок робастного регулятора может быть уменьшен, если вместо робастного алгоритма адаптации высокого порядка использовать нелинейную обратную связь вида

	(6.365)
	(6.366)

где тройка 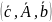является минимальной реализацией передаточной функции с произвольным гурвицевым полиномом степени , а и – постоянные коэффициенты.

Теорема 6.19. Рассматривается замкнутая система, состоящая из объекта (6.343), эталонной модели (6.344), вспомогательных фильтров (6.203), (6.204), настраиваемого регулятора (6.353) и нелинейного робастного алгоритма высокого порядка (6.365), (6.366). Если

(6.367)

где

– произвольная положительная константа, – верхняя оценка параметра , а симметрическая положительно определенная матрица является решением уравнения , то для любых и произвольных начальных условий все сигналы являются ограниченными и дополнительно 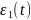, экспоненциально сходятся к установившемуся множеству

(6.368)

где и – некоторые положительные константы и

Пример 6.7. Рассмотрим объект (6.360), эталонную модель (6.201) с и и настраиваемый регулятор (6.265). Робастный алгоритм адаптации высокого порядка (6.365), (6.366) определим уравнениями

	(6.369)
	(6.370)

Тогда условия (6.367) принимают вид ; выбираем .

С учетом (6.369) и (6.370) производные и , необходимые для реализации управления (6.266), могут быть представлены в виде

	(6.371)
	(6.372)

Структура робастного регулятора полностью описывается уравнениями (6.263) – (6.266), (6.369) – (6.372). Общий динамический порядок регулятора равен 18.