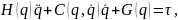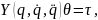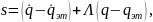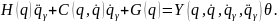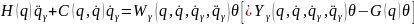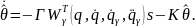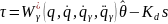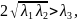Реферат_Тема_17

МИНОБРНАУКИ РОССИИ

САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ

ЭЛЕКТРОТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

«ЛЭТИ» ИМ. В.И. УЛЬЯНОВА (ЛЕНИНА)

КАФЕДРА САУ

РЕФЕРАТ

по дисциплине «Нелинейное и адаптивное управление в технических системах»

Тема: Адаптивные системы управления многостепенными нелинейными механическими объектами, построенные по методу вычисленного момента

Студент гр. ХХХХХХХХХ		ХХХХХХХХХ
Преподаватель		ХХХХХХХХХ

Санкт-Петербург

2024

17.1. Основная структура адаптивного управления многостепенным нелинейным механическим объектом, построенная по методу вычисленного момента

Пусть многостепенной нелинейный механический объект описывается системой, состоящей из и дифференциальных уравнений второго порядка в форме Лагранжа (n - число степеней подвижности механического объекта), объединенных в векторно-матричное уравнение вида

(4.19)

где 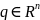– вектор обобщенных координат; – вектор управляющих сил (моментов); – n × n-матрица инерции; – n × n-матрица центробеж-ных и кориолисовых сил; 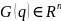– вектор гравитационных сил. Уравнение (4.19) допускает (квази)линейную параметризацию относительно вектора специально подобранных неизвестных массоинерционных параметров объекта в виде:

(4.20)

где – вектор неизвестных постоянных массоинерционных параметров объекта; 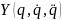– известная n × m-матричная нелинейная функция, называе-мая регрессором.

Обозначим через вектор линейную комбинацию ошибок по обобщенным скоростям и обобщенным положениям (координатам), вида:

(4.21)

где 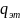, 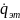– векторы эталонных положений и скоростей соответственно, 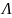– симметричная, в частности, диагональная числовая положительными собст-венными значениями. Введём также виртуальную переменную («задающую траекторию») вида

(4.22)

В силу определения регрессора из (4.19), (4.20) следует тождество вида

(4.23)

Используя введенные соотношения (4.20)–(4.23), адаптивный закон управления объектом (4.19) в форме алгоритма вычисленного момента будет иметь следующий вид:

(4.24)

а регуляризованные алгоритмы параметрической настройки будут выражаться дифференциальными уравнениями вида

(4.25)

где , , – симметричные, в частности, диагональные числовые матрицы соответствующих размерностей с положительными собственными значениями.

Адаптивное управление вида (4.24), (4.25) обеспечивает диссипативность в целом системы (4.19) – (4.25) по переменным

(4.26)

Адаптивный закон (4.24) вычисленного момента с алгоритмами параметрической настройки (4.25), как и алгоритмы скоростного градиента, рассчитаны на полное знание нелинейной структуры уравнений объекта (4.19) и предполагают точное «копирование» всех нелинейностей в построении регрессора (4.20), а также точный учет конечного числа 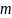неизвестных параметров 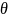объекта, причем полагаемых постоянными.

17.2. Упрощение адаптивных алгоритмов вычисленного момента в управлении нелинейным механическим объектом

Рассмотрим три способа упрощения адаптивных алгоритмов вычисленного момента вида (4.24), (4.25), основанных на упрощении нелинейной структуры матричной функции.

Первый способ упрощения алгоритмов (4.24), (4.25) основан на исключении из используемой в адаптивном законе управления (4.24) матрицы регрессора (4.20) заведомо ограниченных членов, какими являются члены, попадающие в матрицу из вектора . Для этого случая введем соотношение

(4.27)

и запишем следующий адаптивный закон управления и алгоритмы настройки его параметров:

	(4.28)
	(4.29)

Утверждение 1. Адаптивная система, определяемая уравнениями (4.19), (4.27), (4.28), (4.29), диссипативна в целом по переменным вида (4.8).

Второй способ упрощения адаптивных алгоритмов (4.24), (4.25) связан с аппроксимацией нелинейных членов, отвечающих матрице инерции .

Для этого выберем некоторую матрицу так, чтобы матрица была положительно определённой. Заметим, что в силу свойства глобальной ограниченности такой выбор возможен всегда. Для этого случая введём следующее соотношение:

(4.30)

Утверждение 2. Для объекта (4.19) закон адаптивного управления вида

(4.31)

с алгоритмами настройки

(4.32)

обеспечивает глобальную диссипативность по переменным (4.26), если выполнено условие

(4.33)

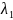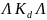где , – наименьшие собственные значения матриц и соответственно, – наибольшее собственное значение матрицы .

Третий способ упрощения адаптивных алгоритмов (4.24), (4.25) вычисления момента основан на применении метода мажорирующих функций и состоит в замене матричной функции регрессора в алгоритмах адаптивного управления (4.24), (4.25) на соответствующую ей мажорирующую матричную функцию. Такая функция может быть построена с помощью замены ограниченных членов, входящих мультипликативно по отношению к остальным членам соответствующего элемента , их верхними по модулю гранями. Таким способом удается избавится, по крайней мере от тех тригонометрических функций, которые могут быть вынесены за скобку в соответствующем элементе матрицы .

Утверждение 3. Пусть объект управления описывается уравнением (4.19), а закон адаптивного управления и алгоритмы настройки имеют вид соответственно

	(4.34)
	(4.35)

где – матричная функция, мажорирующая для . Тогда адаптивная система управления (4.19), (4.34), (4.35) диссипативна в целом по переменным (4.26).

Это утверждение может быть использовано также для упрощения нелинейной структуры членов, соответствующих матрице центробежных и кориолисовых сил .