Реферат_Тема_13

МИНОБРНАУКИ РОССИИ

САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ

ЭЛЕКТРОТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

«ЛЭТИ» ИМ. В.И. УЛЬЯНОВА (ЛЕНИНА)

КАФЕДРА САУ

РЕФЕРАТ

по дисциплине «Нелинейное и адаптивное управление в технических системах»

Тема: Адаптивное и робастное управление по выходу (метод последовательного компенсатора)

Студент гр. ХХХХХХХХХ		ХХХХХХХХХ
Преподаватель		ХХХХХХХХХ

Санкт-Петербург

2024

13.1. Адаптивная стабилизация нелинейной системы с ограни-ченными функциональными неопределенностями

Постановка задачи

Рассмотрим нелинейный объект управления вида

(4.55)

где – вектор состояний системы (4.55), – неизвестные матрицы, причем пара полностью управляема, а пара полностью наблюдаема; нелинейность представима в виде

(4.56)

где – неизвестный вектор постоянных параметров, – неизвестная, ограниченная функция для всех и .

Будем предполагать, что вектор переменных состояния системы (4.55) не измеряется, а измеряется только выходная переменная . Для простоты ограничимся рассмотрением случая, когда , и обозначим . Тогда модель (4.55) примет вид

(4.57)

Запишем систему (4.57) в форме «вход-выход»:

(4.58)

где – гурвицев полином степени , – полином степени (может быть неустойчивым), – полином степени (может быть неустойчивым); коэффициенты предполагаются неизвестными.

В качестве цели управления зададимся решением задачи расчета закона управления, обеспечивающего выполнение условия

(4.59)

где число задается разработчиком системы управления.

Синтез алгоритма управления

Рассмотрим систему вида

(4.60)

Предположим, что производные выходного сигнала измеряются. Выберем закон управления вида

(4.61)

где – гурвицев полином степени ; – новое, задачно-ориентированное управление.

Тогда модель (4.60) примет вид

(4.62)

где – гурвицев полином; относительная степень модели (4.62) равна единице ( ), функция .

Выберем закон управления вида

(4.63)

где , коэффициент предназначен для компенсации неопределенности .

Тогда при определенных значениях коэффициента становится гурвицевым полином

(4.64)

Однако закон управления (4.61) не может быть реализован из-за невозможности измерения производных выходной переменной . Воспользуемся линейной версией метода последовательного компенсатора и преобразуем закон управления (4.61) следующим образом:

(4.65)

где коэффициент и полином выбираются таким образом, чтобы полином (4.64) был гурвицевым; – функция, формируемая алгоритмом вида

	(4.66)
	(4.67)

где ; – коэффициенты, рассчитываемые из соображения асимпто-тической устойчивости (4.66) при .

Закон управления (4.65) является технически реализуем, так как содержит измеряемые и известные сигналы. Подставляя закон управления (4.65) в (4.60), получаем

(4.68)

где – функция отклонения (невязка).

Проведем преобразование модели (4.68):

(4.69)

где ограничена в силу того, что степень числителя передаточной функции не превосходит степени знаменателя.

Принимая обозначения и , для системы (4.69) получаем

(4.70)

Представим модель “вход-выход” (4.70) в виде модели “вход-состояние-выход”:

(4.71) (4.72)

Перепишем модель (4.66)–(4.67) в векторно-матричной форме:

(4.74) (4.75)

Введем в рассмотрение вектор отклонений

(4.76)

тогда в силу структуры матрицы невязка примет вид

(4.77)

Для производной от получим

(4.78)

Так как 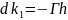, то

(4.74) (4.75)

Теорема 4.2. Существует число такое, что все траектории системы (4.71), (4.72), (4.79), (4.80) ограничены и за счет выбора параметра могут быть сведены в любую малую окрестность ∆.

13.2. Адаптивное управление нелинейной системой с ограниченными функциональными неопределенностями в условиях действия возмущающих воздействий

Постановка задачи

Рассмотрим нелинейный объект управления вида

(4.94)

где – вектор переменных состояния системы, пара полностью управляема, а пара полностью наблюдаема; нелинейность представима в виде (4.56), а – неизвестное ограниченное возмущение.

Запишем систему (4.94) в форме «вход-выход»:

(4.95)

В качестве цели управления зададимся решением задачи слежения с заданной точностью выхода объекта управления (4.95) за командным сигналом , т. е.

(4.97)

Выдвинем следующие допущения, при которых цель управления будет выполнена.

Допущение 4.1. Измеряется только выходная переменная , но не ее производные.

Допущение 4.2. Будем полагать, что эталонный сигнал и все его производные ограничены.

Допущение 4.3. Будем полагать, что возмущение и его производные ограничены.

Допущение 4.4. Степень полинома не превышает степени полинома .

Рассмотрим задачу обеспечения желаемого поведения нелинейной системы (4.94). Пусть ошибка слежения имеет вид

(4.98)

Тогда, подставив в (4.98) уравнение (4.95), получаем

(4.99)

где сигнал

ограничен в силу гурвицевости полинома , условия (4.56), а также допущений 4.2, 4.3 и 4.4.

Таким образом, задача слежения выхода объекта (4.95) за командным сигналом сводится к проблеме стабилизации модели (4.59).

Синтез алгоритма адаптивного управления

Выберем закон управления вида

(4.100)

где – функция, формируемая алгоритмом оценки вида

	(4.101)
	(4.102)

Закон управления (4.100) является технически реализуем, так как содержит измеряемые и известные сигналы. Подставляя (4.100) в (4.99), получаем

(4.103)

где .

Преобразуем уравнение (4.103) следующим образом:

Принимая обозначения и , получаем

(4.104)

Представим модель “вход-выход” (4.104) в виде модели “вход-состояние-выход”:

(4.105) (4.106)

Перепишем (4.101), (4.102) в векторно-матричной форме

(4.108) (4.109)

Введем в рассмотрение вектор отклонений

(4.110)

тогда в силу структуры матрицы невязка примет вид

(4.111)

Для производной от получим

(4.112)

Так как , то

(4.113) (4.114)

Теорема 4.3. Существует число такое, что все траектории системы (4.105), (4.106), (4.113), (4.114) ограничены и за счет выбора параметра могут быть сведены в любую малую окрестность .

13.3. Адаптивное и робастное управление по выходу нелинейными системами в условиях секторных ограничений на нелинейность

Постановка задачи

Рассмотрим нелинейную систему в форме “вход-состояние-выход”:

(4.125) (4.126)

Будем полагать, что измеряется только выходная переменная системы (4.125), (4.126).

Представим нелинейную систему (4.125), (4.126) в форме «вход-выход»:

(4.127)

Цель управления: используя только измерения выхода, найти закон управления, обеспечивающий стремление выходной переменной объекта управления к нулю при 𝑡 → ∞.

Алгоритм управления

Выберем закон управления для стабилизации системы (4.125)–(4.127) в соответствии с методом последовательного компенсатора:

(4.129)

где является оценкой выхода модели (4.127) и формируется алгоритмом вида

	(4.130)
	(4.131)

Закон управления (4.129)–(4.131) является технически реализуем, так как содержит измеряемые и известные сигналы.

Подставляя (4.129) в уравнение (4.127), получаем

(4.132)

Проводя преобразования для (4.132), имеем

принимая обозначения и , для системы (4.132) получаем

(4.133)

где невязка равна

Представим модель “вход-выход” (4.133) в виде модели “вход-состояние-выход”:

(4.134) (4.135)

Перепишем (4.130), (4.131) в векторно-матричной форме

Введем в рассмотрение вектор отклонений . Тогда в силу структуры матрицы невязка примет вид

Для производной от получим

Так как , то

(4.137) (4.138)

Теорема 4.4. Пусть полином гурвицев, порядок полинома , число выбрано так, что выполнено условие (4.136), и функция удовлетворяет следующим допущениям:

для любых где . Тогда существует число такое, что система (4.134), (4.135), (4.137), (4.138) экспоненциально устойчива.

Настройка коэффициентов регулятора

Для настройки коэффициентов воспользуемся алгоритмами вида

(4.150)

где , а функция рассчитывается следующим образом:

где

Выберем следующим образом:

(4.151)

где .