Реферат_Тема_12

МИНОБРНАУКИ РОССИИ

САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ

ЭЛЕКТРОТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

«ЛЭТИ» ИМ. В.И. УЛЬЯНОВА (ЛЕНИНА)

КАФЕДРА САУ

РЕФЕРАТ

по дисциплине «Нелинейное и адаптивное управление в технических системах»

Тема: Адаптивное управление с неявной эталонной моделью. Метод шунтирования

Студент гр. ХХХХХХХХХ		ХХХХХХХХХ
Преподаватель		ХХХХХХХХХ

Санкт-Петербург

2024

6.6.1. Синтез адаптивной системы для строго минимально-фазового объекта

Рассмотрим объект, описываемый уравнениями состояния

(6.391)

где – вектор состояний объекта, – скалярное управление, – вектор измеряемых выходов, , , – матрицы соответствующих размерностей, зависящие от вектора неизвестных параметров . Задан линейный регулятор с настраиваемыми коэффициентами

(6.392)

где . Поставим задачу найти алгоритм адаптации

(6.393)

такой, что для любого в системе (6.391), (6.393) достигалась цель управления

(6.394)

а траектории системы были ограничены. Поставленную задачу будем решать методом скоростного градиента. Для этого зададим цель управления (6.394) соотношением при , где – оценочная функция, – положительно определенная матрица. Найдем функцию – производную в силу (6.391), а затем . Имеем:

	(6.395)
	(6.396)

Поскольку алгоритм адаптации должен использовать только измеряемые величины, в (6.396) скаляр должен быть функцией вектора выходов . Так как и линейны по , то должен быть линейной комбинацией выходов, т. е. для некоторого и любого . Последнее означает, что . Таким образом, мы пришли к алгоритму адаптации

(6.397)

где – l × l-матрица.

Теорема 6.21. Система (6.391), (6.392), (6.397) адаптивна в классе по отношению к цели управления (6.394) и все её траектории ограничены, если для любого функция строго минимально-фазовая, где – передаточная матрица объекта (6.391).

Условия теоремы 6.21 достаточны для существования у системы (6.391)–(6.393) функции вида

(6.398)

где – n × n-матрица, – l × l-матрица, , обладающей свойством

(6.399)

Теорема 6.22. Пусть . Для существования у системы (6.391)–(6.393) функции Ляпунова вида (6.398) со свойством (6.399) необходимо и достаточно, чтобы алгоритм адаптации имел вид (6.397), а многочлен был гурвицевым степени с положительными коэффициентами.

Теорема 6.22 показывает, что алгоритмами вида (6.397) исчерпываются все алгоритмы, которые могут быть получены с помощью функции Ляпунова (6.398), и синтезировать еще какие-либо алгоритмы, используя данную функцию Ляпунова, невозможно.

6.6.2. Синтез адаптивной системы для строго минимально-фазового многоканального объекта

Распространим полученные результаты 6.6.1 на многосвязные системы, т. е. на объекты с несколькими управляющими воздействиями. Для описания объекта и регулятора сохраним уравнения (6.391), (6.392), в которых будем считать, что – l × m-матрица, – n × m-матрица. Пере-даточная матрица теперь будет иметь порядок l × m. В случае вместо алгоритма (6.397) будем рассматривать алгоритм

(6.400)

где – столбцы матрицы настраиваемых параметров – l × l-матрицы. В алгоритме (6.400) для настройки каждого столбца матрицы по существу используется алгоритм вида (6.397), параметры которого (вектор и матрица ) свои для каждого столбца.

Теорема 6.23. Система (6.391), (6.392), (6.400) адаптивна в классе по отношению к цели управления (6.394), если класс определяется условием: для любого матрица 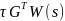– гипер-минимально-фазовая при некоторой

Теорема 6.24. Пусть передаточная матрица объекта не равна нулю тождественно, а ранг матрицы . Для существования у системы (6.391)– (6.393) функции Ляпунова вида

(6.401)

где при , необходимо и достаточно, чтобы алгоритм адаптации имел вид (6.400), а матрица была гипер-минимально фазовой при некоторой

6.6.3. Общий случай. Метод шунтирования

Перейдем к рассмотрению случая произвольного значения относительной степени объекта. Для любого минимально-фазового объекта со скалярной относительной степенью существует параллельный компенсатор порядка , включение которого эквивалентно превращению объекта в гипер-минимально-фазовый ( ). Это позволяет применить алгоритм адаптивной стабилизации с неявной эталонной моделью, описанный выше.

Вновь рассмотрим линейный стационарный объект (6.391) с матричной передаточной функцией . Пусть . Очевидно, строго минимально-фазовая и гипер-минимально-фазовая системы имеют скалярную относительную степень .

Теорема 6.25. Пусть для некоторой l × m-матрицы объект с переда-точной функцией минимально-фазовый и имеет скалярную относительную степень , причем матрица гурвицева. Пусть – гурвицевы многочлены степеней , соответственно, причем знаки коэффициентов и совпадают. Пусть

(6.402)

Тогда существует число и функция такие, что матрица строго минимально-фазовая при .

Лемма 6.9. Пусть – m × m-матричные многочлены с коэффициентами, непрерывными по при

Пусть многочлены гурвицевы.

Тогда многочлен будет гурвицевым при всех достаточно малых .

Следствие 6.3. Пусть многочлены и гурвицевы. Тогда существуют число и функция такие, что многочлен гурвицев при .

Теорема 6.26. Пусть передаточная функция минимально-фазовая для некоторой l × m-матрицы и имеет скалярную относительную степень , причем матрица гурвицева. Пусть – гурвицевы многочлены степеней , соответственно, причем знаки коэффициентов и совпадают. Пусть алгоритм управления имеет вид

	(6.403)
	(6.404)
	(6.405)

Тогда в системе (6.391), (6.404), (6.405) для всех достигается цель (6.394), а также цели

(6.407)