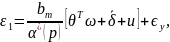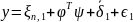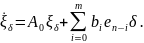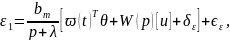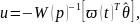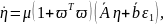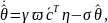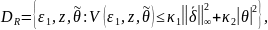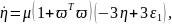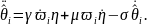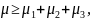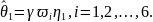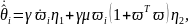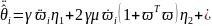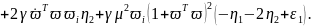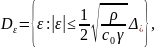Реферат_Тема_11
.docxМИНОБРНАУКИ РОССИИ
САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ
ЭЛЕКТРОТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
«ЛЭТИ» ИМ. В.И. УЛЬЯНОВА (ЛЕНИНА)
КАФЕДРА САУ
РЕФЕРАТ
по дисциплине «Нелинейное и адаптивное управление в технических системах»
Тема: Практикум применения методов адаптивного робастного и нелинейного управления по выходу неопределенными линейными объектами при наличии внешних возмущений
Студент гр. ХХХХХХХХХ |
|
ХХХХХХХХХ |
Преподаватель |
|
ХХХХХХХХХ |
Санкт-Петербург
2024
6.5. Управление по выходу неопределенными линейными объектами при наличии внешних возмущений
В настоящем параграфе будем полагать, что параметрически неопределенный объект управления подвержен воздействию внешнего неизмеряемого возмущения. Рассматриваемый класс линейных стационарных объектов описывается уравнением вида
|
(6.343) |
где
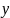 и
и
 – регулируемая переменная и сигнал
управления соответственно,
– регулируемая переменная и сигнал
управления соответственно,
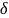 – внешнее ограниченное возмущение,
– внешнее ограниченное возмущение,
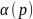 и
и
 – нормированные полиномы с неизвестными
коэффициентами такие, что
– нормированные полиномы с неизвестными
коэффициентами такие, что
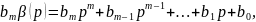

Как и в п. 6.4, примем стандартные допущения 6.6 и определим желаемое поведение регулируемой переменной у с помощью эталонной модели
|
(6.344) |
где
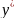 – эталонный выход,
– эталонный выход,
 – сигнал задания,
– сигнал задания,
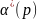 – нормированный гурвицев полином
степени
– нормированный гурвицев полином
степени
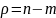 ,
,
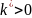 – постоянный коэффициент.
– постоянный коэффициент.
В общем случае присутствие внешнего возмущения не позволяет обеспечить асимптотического слежения за эталонным выходом . Поэтому в качестве цели управления потребуем обеспечения ограниченности всех сигналов в замкнутой системе и слежения за эталонным выходом с определенной степенью точности. Во многих практических случаях выполнение такой цели управления является вполне достаточным.
6.5.1. Параметризованная модель объекта управления
Присутствие внешнего возмущения несколько изменяет параметризованные модели, полученные в 6.4.2. Влияние внешнего возмущения определяется следующими двумя леммами.
Лемма
6.7. Рассмотрим вместе с объектом
(6.343) и эталонной моделью (6.344) вспомогательные
фильтры (6.203) и (6.204). Тогда для любого
нормированного гурвицева полинома
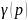 степени
степени
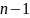 ошибка слежения
ошибка слежения
 может быть представлена в виде
может быть представлена в виде
|
(6.345) |
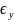 – экспоненциально затухающая функция
времени,
– экспоненциально затухающая функция
времени,
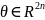 – вектор постоянных неизвестных
параметров,
– вектор постоянных неизвестных
параметров,
 – ограниченная функция времени, зависящая
от
,
и
– ограниченная функция времени, зависящая
от
,
и
 .
.
Лемма
6.8. Вместе с объектом (6.343) рассмотрим
вспомогательные фильтры (6.209). Тогда
регулируемая переменная
и ее первая производная
 могут быть представлены в форме следующих
параметризованных моделей:
могут быть представлены в форме следующих
параметризованных моделей:
|
(6.346) |
и
|
(6.347) |
где, как и в лемме 6.6,


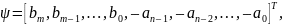


 и
и
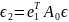 экспоненциально затухают,
экспоненциально затухают,
 и
и
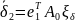 – ограниченные функции времени, зависящие
от
,
а
– ограниченные функции времени, зависящие
от
,
а
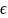 и
и
 удовлетворяют условиям
удовлетворяют условиям
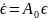 и
и
|
(6.348) |
6.5.2. Робастное управление с использованием алгоритмов адаптации высокого порядка
В настоящем параграфе для построения алгоритмов робастного управления линейным объектом по выходу в условиях присутствия внешних возмущений будут использованы методы синтеза, представленные теоремами 6.12 и 6.13.
Сначала,
как и в 6.4.4, выберем передаточную функцию
 с относительной степенью
с относительной степенью
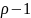 такую, что
такую, что

где
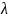 – произвольная положительная константа.
Тогда модель (6.345) может быть представлена
в виде
– произвольная положительная константа.
Тогда модель (6.345) может быть представлена
в виде
|
(6.351) |
где
|
(6.352) |
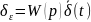 ,
а
,
а
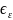 экспоненциально затухает.
экспоненциально затухает.
Настраиваемый регулятор выбирается в стандартном виде
|
(6.353) |
что ведет к получению следующей замкнутой модели ошибки
|
(6.354) |
где
 .
Тогда структура робастного алгоритма
адаптации высокого порядка будет
определяться следующими уравнениями
(см. теорему 6.11):
.
Тогда структура робастного алгоритма
адаптации высокого порядка будет
определяться следующими уравнениями
(см. теорему 6.11):
|
(6.355) |
|
(6.356) |
где
 – минимальная реализация передаточной
функции
– минимальная реализация передаточной
функции
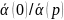 ,
,
 – произвольный асимптотически устойчивый
полином степени
– произвольный асимптотически устойчивый
полином степени
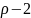 ,
а
,
а
 ,
,
 и
и
 – постоянные коэффициенты.
– постоянные коэффициенты.
Свойства устойчивости замкнутой системы сформулируем в виде следующей теоремы.
Теорема 6.18. Рассмотрим замкнутую систему, состоящую из объекта (6.343), эталонной модели (6.344), вспомогательных фильтров (6.203), (6.204), регулятора (6.353) и робастного алгоритма адаптации высокого порядка (6.355), (6.356). Если
|
(6.357) |
где
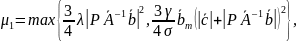
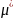 – любая положительная константа,
– любая положительная константа,
 – верхняя оценка коэффициента
– верхняя оценка коэффициента
 ,
а симметрическая положительно определенная
матрица Р является решением уравнения
,
а симметрическая положительно определенная
матрица Р является решением уравнения
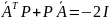 ,
то для любых
,
то для любых
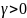 и
и
 и произвольных начальных условий все
сигналы в замкнутой системе являются
ограниченными и, кроме того,
и произвольных начальных условий все
сигналы в замкнутой системе являются
ограниченными и, кроме того,
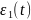 ,
,
 и
и
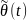 экспоненциально сходятся к установившемуся
множеству
экспоненциально сходятся к установившемуся
множеству
|
(6.358) |
где
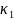 и
и
 – некоторые положительные константы
и
– некоторые положительные константы
и
|
(6.359) |
Пример 6.6. Изменим условия примера 6.4, добавив внешнее возмущение. То есть, рассмотрим следующий объект управления
|
(6.360) |
где параметры
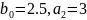 и
и
 полагаются неизвестными, в то время как
верхняя оценка
полагаются неизвестными, в то время как
верхняя оценка
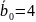 считается априорно известной.
считается априорно известной.
Используем следующий робастный алгоритм адаптации высокого порядка
|
(6.361) |
|
(6.362) |
Выберем
 .
Из условия (6.357) получаем
.
Из условия (6.357) получаем
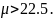 Выберем
Выберем
 .
.
|
(6.363) |
Таким образом, структура регулятора с робастным алгоритмом адаптации высокого порядка полностью описывается уравнениями (6.263)–(6.266), (6.361)–(6.363). Общий динамический порядок регулятора равен 23 и, следовательно, является более низким по сравнению с неробастным регулятором из примера 6.4.
Теорема 6.19. Рассмотрим замкнутую систему, состоящую из объекта (6.343), эталонной модели (6.344), вспомогательных фильтров (6.203), (6.204), настраиваемого регулятора (6.353) и нелинейного робастного алгоритма высокого порядка (6.365), (6.366). Если
|
(6.367) |
где

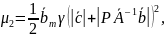
 – произвольная положительная константа,
– верхняя оценка параметра
,
а симметрическая положительно определенная
матрица
– произвольная положительная константа,
– верхняя оценка параметра
,
а симметрическая положительно определенная
матрица
 является решением уравнения
,
то для любых
и произвольных начальных условий все
сигналы являются ограниченными и
дополнительно
,
экспоненциально сходятся к установившемуся
множеству
является решением уравнения
,
то для любых
и произвольных начальных условий все
сигналы являются ограниченными и
дополнительно
,
экспоненциально сходятся к установившемуся
множеству
|
(6.368) |
где и – некоторые положительные константы и
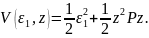
Пример
6.7. Рассмотрим объект (6.360), эталонную
модель (6.201) с
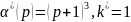 и
и
 и настраиваемый регулятор (6.265). Робастный
алгоритм адаптации высокого порядка
(6.365), (6.366) определим уравнениями
и настраиваемый регулятор (6.265). Робастный
алгоритм адаптации высокого порядка
(6.365), (6.366) определим уравнениями
|
(6.369) |
|
(6.370) |
Тогда условия (6.367) принимают вид
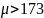 ;
выбираем
;
выбираем
 .
.
С
учетом (6.369) и (6.370) производные
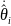 и
и
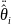 ,
необходимые для реализации управления
(6.266), могут быть представлены в виде
,
необходимые для реализации управления
(6.266), могут быть представлены в виде
|
(6.371) |
|
(6.372) |
Структура робастного регулятора полностью описывается уравнениями (6.263) – (6.266), (6.369) – (6.372). Общий динамический порядок регулятора равен 18.
Теорема
6.20. Рассмотрим замкнутую систему
управления, состоящую из объекта (6.343),
эталонной модели (6.344), вспомогательных
фильтров (6.209) и робастного регулятора
(6.381). Тогда для любых
и произвольных начальных условий все
сигналы являются ограниченными и
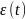 экспоненциально сходится к установившемуся
множеству
экспоненциально сходится к установившемуся
множеству
|
(6.384) |
где
|
(6.385) |
|
(6.386) |
Радиус множества (6.384) может быть сделан
произвольно малым за счет увеличения
или
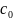 .
.
Пример 6.8. Рассмотрим объект (6.360)
|
(6.387) |
с неизвестными параметрами , и эталонную модель (6.201) с и . С использованием вспомогательных фильтров (6.335) – (6.338), производная ошибки слежения может быть представлена в виде (см. также (6.339))
|
(6.388) |
На
первом шаге процедуры синтеза сигнал
 рассматривается в качестве управления
в (6.388) и выбирается первая функция
стабилизации
рассматривается в качестве управления
в (6.388) и выбирается первая функция
стабилизации
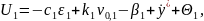
где нелинейная обратная связь имеет вид
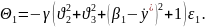
На
втором шаге вводится новая регулируемая
переменная
 и выбирается вторая функция стабилизации
и выбирается вторая функция стабилизации
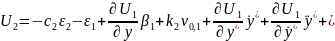
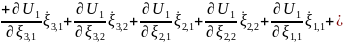
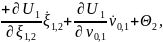
где нелинейная обратная связь имеет вид

Действительное управление выбирается на третьем шаге в виде
|
(6.389) |
где
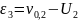 ,
а нелинейная обратная связь определяется
выражением
,
а нелинейная обратная связь определяется
выражением
|
(6.390) |
Структура синтезированного регулятора полностью описывается уравнениями (6.335) – (6.338), (6.389), (6.390). Его общий динамический порядок равен 12 и может быть сокращен до 6 с использованием следствия 6.2. Однако из представленных выражений видно, что для формирования управления необходимы существенные вычислительные затраты.