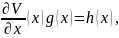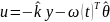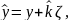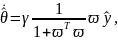Реферат_Тема_9

МИНОБРНАУКИ РОССИИ

САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ

ЭЛЕКТРОТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

«ЛЭТИ» ИМ. В.И. УЛЬЯНОВА (ЛЕНИНА)

КАФЕДРА САУ

РЕФЕРАТ

по дисциплине «Нелинейное и адаптивное управление в технических системах»

Тема: Управление по выходу. Методы адаптивного управления строго пассивными и строго минимально фазовыми объектами. Адаптивные алгоритмы с расширенной ошибкой и высоких порядков

Студент гр. ХХХХХХХХХ		ХХХХХХХХХ
Преподаватель		ХХХХХХХХХ

Санкт-Петербург

2024

1. Управление строго пассивными и строго минимально фазовыми объектами.

Сначала попробуем использовать базовую схему адаптивной стабилизации, представленную теоремой 6.1. Как хорошо известно, это можно сделать при следующих дополнительный предположениях.

Допущение 6.4. Существует гладкая, положительно определенная функция (функция Ляпунова) V(x) такая, что

	(1)
	(2)

где – положительно определенная функция и дополнительно при .

Условие (1) позволяет исключить из закона управления (6.21) стабилизирующую обратную связь по состоянию , а условие (2) позволяет использовать в алгоритме адаптации (6.22) доступную прямым измерениям выходную переменную вместо . Таким образом, с учетом допущения 6.4 стабилизирующий алгоритм адаптивного управления (6.21), (6.22) принимает вид

	(3)
	(4)

При этом замкнутая система управления будет описываться уравнениями

	(5)
	(6)

где . Свойства устойчивости замкнутой системы могут быть установлены с использованием функции Ляпунова

Для системы (5), (6) с учетом (1), (2) имеем

Следовательно, и являются ограниченными. Если, дополнительно, регрессор – ограниченная функция, то правые части (5), (6) являются локально липшицевыми по и равномерно по . Тогда в силу теоремы 2.18 при . Таким образом, доказана следующая теорема, которая может рассматриваться в качестве нелинейного обобщения результатов, полученным П. Парксом.

Теорема 6.8 (адаптивная стабилизация по выходу строго пассивной системы). Пусть выполняются допущения 6.3 и 6.4. Тогда закон управления (3), (4) обеспечивает для объекта (6.120), (6.121) при любых и произвольных начальных условиях ограниченность и . Если регрессор ограничен, то, дополнительно, все сигналы в замкнутой системе ограничены и

Основной вопрос, который возникает в связи с представленными результатами: насколько ограничительным является допущение 6.4? Как было показано в 2.6.3, условия (1), (2) выполняются только в том случае, если система

	(7)
	(8)

является строго пассивной. В частности, это означает, что относительная степень системы (7), (8) равна единице, а состояние равновесия 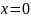автономной части уравнения (7) является асимптотически устойчивым. Таким образом, необходимо признать, что допущение 6.4 является крайне ограничи-тельным и как следствие – теорема 6.8 имеет ограниченное практическое значение.

Следующая теорема предлагает простую модификацию алгоритма адаптивного управления по выходу, позволяющую распространить указанный метод управления на более широкий класс строго минимально фазовых систем (следует отметить, что в отличие от строго пассивных систем данный класс включает неустойчивые системы).

Теорема 6.9 (адаптивная стабилизация по выходу строго минимально фазовой системы). Рассмотрим закон управления

(9)

и алгоритмы адаптации вида

	(10)
	(11)

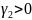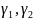где является вектором настраиваемых параметров, – настраиваемый коэффициент обратной связи, и – постоянные коэффициенты. Если числитель передаточной функции (6.133) системы (6.130), (6.131) является гурвицевым полиномом и , то адаптивный регулятор (9) – (10) обеспечивает для объекта управления (6.130), (6.131) при любых и произвольных начальных условиях ограниченность и . Если регрессор ограничен, то, дополнительно, все сигналы в замкнутой системе ограниченными и

2. Методы адаптивного управления с расширенной ошибкой.

При построении систем адаптивного управления с расширенной ошибкой структура настраиваемого регулятора определяется в соответствии с принципом непосредственной компенсации

(12)

а алгоритм адаптации выбирается интегрального типа

(13)

где функция настройки будет определена позже. После подстановки (12) и (13) в (6.130), (6.131) модель замкнутой системы принимает вид

	(14)
	(15)

где . Для того, чтобы синтезировать алгоритм адаптации (13), который использует только доступную измерениями выходную переменную (а не весь вектор состояния ), воспользуемся понятием расширенной ошибки.

Лемма 6.1 (лемма о расширенной ошибке). Пусть выполняется допущение 6.5. Рассмотрим вместе с моделью (14), (15) вспомогательные фильтры вида

	(16)
	(17)

где вместо производной используется ее аналитическое выражение их алгоритма адаптации (13). Определим расширенную ошибку выражением

(18)

где экспоненциально затухающий член удовлетворяет уравнению с начальными условиями .

Лемма 6.2. Рассмотрим (16), (17) где удовлетворяет допущению 6.5. Если производная – квадратично интегрируемая функция времени (т.е. ), то растет медленнее, чем в том смысле, что

Иногда удобно представить схему расширения сигнала ошибки в терминах передаточных функций.

Лемма 6.3 (схема расширения в терминах передаточных функций). Рассмотрим представление системы (14) в виде модели “вход–выход”

(19)

где передаточная функция удовлетворяет допущению 6.5. Одновременно с (19) рассмотрим вспомогательный фильтр

(20)

и определим расширенную ошибку в виде

(21)

Тогда справедливо следующее соотношение:

(22)

где – “отфильтрованный” регрессор, а – экспоненци-ально затухающая функция времени, вызванная ненулевыми начальными условиями.

Лемма 6.4 (схема расширения с неизвестным коэффициентом). Рассмотрим систему

(23)

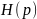где – неизвестный постоянный коэффициент, а передаточная функция удовлетворяет допущению 6.5. Одновременно с (23) рассмотрим вспомогательный фильтр (20) и определим расширенную ошибку в виде

(24)

где – дополнительный настраиваемый параметр. Тогда справедливо следую-щее соотношение:

где , а – экспоненциально затухающая функция времени, вызванная ненулевыми начальными условиями.

Теорема 6.10 (адаптивное управление с расширенной ошибкой). Пусть выполняются допущения 6.3 и 6.5. Рассмотрим настраиваемый регулятор (12) и следующий алгоритм адаптации

(25)

где и определены уравнениями (16) – (18) или (20) – (21), а – постоянный коэффициент. Тогда замкнутая систем управления (6.130), (6.131), (12) и (25) обладает следующими свойствами устойчивости:

1. для любых и произвольных начальных условий вектор настраиваемых параметров является ограниченным, а скорость его изменения – ограниченная и квадратично интегрируема функция времени (т.е. );

2. если регрессор ограничен, то дополнительно к (1) все сигналы в замкнутой системе ограничены, величина – квадратично интегрируемая функция времени (т.е. ) и при .

3. Методы управления с алгоритмами адаптации высоких порядков.

Теорема 6.11 (алгоритм адаптации высокого порядка). Пусть задана модель ошибки (6.166), где , а первые произвольных являются доступными для прямых измерений. Выберем нормированный асимптотически устойчивый полином степени и минимальную реализацию передаточной функции , т.е. 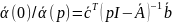. Определим алгоритм адаптации порядка в виде

(26) (27) (28)

где а – постоянный коэффициент. Тогда замкнутая система (6.166), (26) – (28) имеет следующие свойства устойчивости:

1. если

(29)

где – верхняя оценка коэффициента , а матрица является решением уравнения , то для любых начальных условий сигналы , и ограничены ( ), а - и -нормы регулируемой переменной удовлетворяют оценкам

	(30)
	(31)

где является начальным значением функции вида

(32)

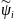при этом переменные и определены равенствами

	(33)
	(34)

2. если регрессор ограничен, то дополнительно к (1) все сигналы в замкнутой системе являются ограниченными и при .

Теорема 6.13 (нелинейный робастный алгоритм высокого порядка). Пусть задана модель ошибки (6.166), где первые производные доступны измерениям. Выберем нормированный асимптотически устойчивый полином степени и минимальную реализацию передаточной функции . Рассмотрим нелинейный робастный алгоритм высокого порядка вида

(35) (36)

где и – постоянные коэффициенты. Тогда замкнутая система (6.166), (35) и (36) обладает следующими свойствами устойчивости:

1. если

(37)

где

– произвольная положительная константа, – верхняя оценка коэффициента , а матрица является решением уравнения , то для любых и произвольных начальных условий и ограничены и экспоненциально сходятся к инвариантному множеству

(38)

где

(39)

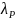– максимальное собственное число матрицы ;

2. если регрессор ограничен, то дополнительно к (1) все сигналы в замкнутой системе также ограничены.