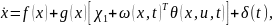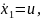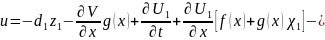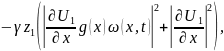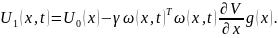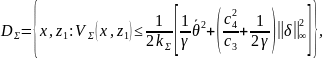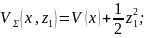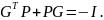МИНОБРНАУКИ РОССИИ
САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ
ЭЛЕКТРОТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
«ЛЭТИ» ИМ. В.И. УЛЬЯНОВА (ЛЕНИНА)
КАФЕДРА САУ
РЕФЕРАТ
по дисциплине «Нелинейное и адаптивное управление в технических системах»
Тема: Итеративные процедуры синтеза нелинейного, адаптивного и
робастного управления нелинейными системами при нарушении
условий согласования (методы адаптивного обхода интегратора)
Студент гр. ХХХХХХХХХ |
|
ХХХХХХХХХ |
Преподаватель |
|
ХХХХХХХХХ |
Санкт-Петербург
2024
1. Методы управления нелинейными неопределенными объектами по состоянию при нарушении условий согласования: метод робастного обхода интегратора (двухшаговая итеративная процедура синтеза).
Итерационные процелуры синтеза.
Для того чтобы определить класс систем, не удовлетворяющих условию согласования, дополним систему (6.18) одним интегратором
|
(1.1) |
|
(1.2) |
где
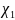 – дополнительная переменная состояния.
В модели (1.1), (1.2) неизвестный вектор
– дополнительная переменная состояния.
В модели (1.1), (1.2) неизвестный вектор
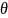 и сигнал управления
и сигнал управления
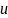 появляются в разных уравнениях и не
являются согласованными. Причем вектор
появляется "на один интегратор выше",
чем
.
Поэтому в системах вида (1.1), (1.2) нарушение
условий согласования характеризуется
уровнем неопределенности, т.е. числом
интеграторов, "расположенных между"
неопределенностями и управлением.
Уровень неопределенности системы (1.1),
(1.2) равен единице.
появляются в разных уравнениях и не
являются согласованными. Причем вектор
появляется "на один интегратор выше",
чем
.
Поэтому в системах вида (1.1), (1.2) нарушение
условий согласования характеризуется
уровнем неопределенности, т.е. числом
интеграторов, "расположенных между"
неопределенностями и управлением.
Уровень неопределенности системы (1.1),
(1.2) равен единице.
Принцип непосредственной компенсации не может быть применен для управления моделью (1.1), (1.2). Поэтому необходимо использовать более гибкие методы синтеза, позволяющие преодолеть структурное препятствие, вызванное нарушением условия согласования. Такие методы, представляющие собой итеративные процедуры синтеза, будут сформулированы ниже в виде трех теорем. Итеративный характер данных процедур означает, что синтез управления осуществляется последовательно, в несколько шагов. На каждом очередном шаге выбирается фиктивный (виртуальный) закон управления - функция стабилизации, обеспечивающий стабилизацию некоторой динамической системы пониженной размерности. Искомое управление определяется на последнем шаге через все предыдущие функции стабилизации.
Начнем с нелинейного робастного управления. А именно – продемонстрируем, как метод синтеза теоремы 6.3 может быть распространен на систему (1.1), (1.2).
Теорема
6.5 (робастный обход интегратора). Пусть
выполняются допущения 6.1 и 6.2 и,
дополнительно, функция
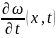 является локально липшицевой по
является локально липшицевой по
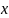 равномерно по
равномерно по
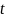 .
Рассмотрим закон управления
.
Рассмотрим закон управления
|
(1.3) |
где
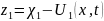 ,
,
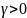 и
и
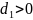 – постоянные коэффициенты, а первая
функция стабилизации
– постоянные коэффициенты, а первая
функция стабилизации
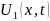 определяется как
определяется как
|
(1.4) |
В этом случае замкнутая система управления (1.1) – (1.4) обладает следующими свойствами устойчивости:
для любых и и произвольных начальных условий
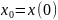 все сигналы являются ограниченными и
все сигналы являются ограниченными и
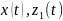 экспоненциально сходятся к инвариантному
множеству:
экспоненциально сходятся к инвариантному
множеству:
|
(1.5) |
где
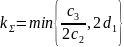 и
и
|
(1.6) |
при этом скорость сходимости быстрее,
чем
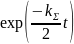 ;
;
если
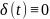 ,
то дополнительно к (1) радиус инвариантного
множества
,
то дополнительно к (1) радиус инвариантного
множества
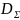 (1.5) может быть сделан произвольно малым
за счет увеличения коэффициента
(1.5) может быть сделан произвольно малым
за счет увеличения коэффициента
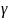 ;
;если и
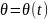 удовлетворяет условию
удовлетворяет условию
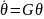 с некоторой гурвицевой матрицей
с некоторой гурвицевой матрицей
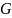 и начальными условиями
и начальными условиями
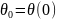 ,
то
,
то
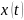 и
и
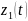 экспоненциально сходятся к нулевым
значениям
экспоненциально сходятся к нулевым
значениям
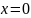 и
и
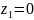 быстрее
быстрее
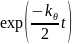 ,
где
,
где
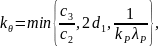
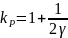 ,
а
,
а
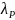 – наибольшее собственное значение
матрицы
– наибольшее собственное значение
матрицы
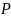 ,
являющемся решением уравнения
,
являющемся решением уравнения
|
(1.7) |
2. Метод адаптивного обхода интегратора с использованием функции настройки (двухшаговая итеративная процедура).