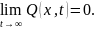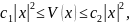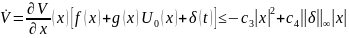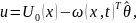Реферат_Тема_6

МИНОБРНАУКИ РОССИИ

САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ

ЭЛЕКТРОТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

«ЛЭТИ» ИМ. В.И. УЛЬЯНОВА (ЛЕНИНА)

КАФЕДРА САУ

РЕФЕРАТ

по дисциплине «Нелинейное и адаптивное управление в технических системах»

Тема: Адаптивное, адаптивное робастное и нелинейное управление нелинейными системами по состоянию: методы непосредственной (адаптивной) компенсации

Студент гр. ХХХХХХХХХ		ХХХХХХХХХ
Преподаватель		ХХХХХХХХХ

Санкт-Петербург

2024

1. Постановка задачи управления неопределенными объектами

Рассматривается объект управления с выходной переменной у, вектором состояния х и сигналом управления u. Пусть поведение объекта зависит от ряда неизвестных факторов – через вектор θ. Предположим, что задано множество , определяющее класс рассматриваемых объектов управления, а также задана цель управления, определяющая желаемый характер поведения замкнутой системы. Во многих случаях цель управления может быть задана в виде целевого неравенства

(1.1)

где 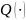– целевая функция, – порог (допустимое значение ).

В случае управления неопределенными объектами необходимо потребовать, чтобы неравенство (1.1) выполнялось, по крайней мере, асимптотически, т. е. в форме предельного целевого неравенства

(1.2)

Задача управления неопределенным объектом: найти закон управления, не содержащий неизвестный вектор θ и в то же время обеспечивающий ограниченность всех сигналов в замкнутой системе, и выполнение предельного целевого неравенства (1.2) для всех .

Возможно также использование закона управления, в явном виде зависящего от θ

(1.3)

Более совершенная стратегия состоит в одновременном изучении объекта и управлении им. С методологической точки зрения, закон управления, решающий задачу одновременного изучения и управления объектом, удобно представить в виде

	(1.4)
	(1.5)

где представляет собой оценку вектора θ, полученную в ходе рабочего функционирования замкнутой системы управления. В зависимости от вида уравнения (1.5) мы будем называть дополнительную обратную связь алгоритмом адаптации или нелинейной робастной обратной связью.

Ограничим наше внимание классом нелинейных систем, описывающихся уравнениями вида

(1.6) (1.7)

где – известная матричная функция, а – неизмеряемое внешнее возмущение.

Понятия, связанные с основными свойствами модели (1.6), (1.7). Три типа неопределенностей математической модели:

1) функциональная неопределенность означает, что θ является неизвестной функцией х и u, т. е. ;

2) сигнальная неопределенность означает, что θ является неизвестной функцией времени, т. е. ;

3) параметрическая неопределенность означает, что θ является вектором неизвестных постоянных параметров.

Будем говорить, что задача управления решается при идеальных условиях, если в системе (1.6), (1.7) отсутствуют внешние возмущения (т. е. ), θ является вектором неизвестных постоянных параметров и динамический порядок реального объекта не выше порядка его модели (отсутствует паразитная динамика). Следует отметить, что при идеальных условиях удается обеспечить выполнение более строгого (по сравнению с (1.2)) целевого условия вида

(1.8)

Переходя к структурным свойствам модели (1.6), (1.7), необходимо выделить два случая, при которых возникают принципиальные теоретические трудности на пути построения соответствующих законов управления. Во-первых, это нарушение так называемых условий согласования и, во-вторых, - высокая относительная степень объекта управления.

Задача адаптивного управления, как правило, решается при идеальных условиях. Алгоритм адаптации представляет собой динамическую обратную связь интегрального типа, что обеспечивает "запоминание" постоянного настроенного значения . Таким образом, алгоритм адаптивного управления может быть описан уравнениями вида

	(1.9)
	(1.10)

где представляет собой вектор настраиваемых параметров регулятора (1.9), дополнительная обратная связь (1.10) называется алгоритмом адаптации, а функция – функцией настройки.

Определение 1.1. Система (1.6), (1.7), (1.9) и (1.10) называется адаптивной в классе по отношению к цели управления (1.8), если при идеальных условиях все сигналы системы являются ограниченными и дополнительно выполняется целевое условие (1.8) для любого постоянного вектора и любых начальных условий .

Для того чтобы обеспечить ограниченность всех сигналов и избежать потери устойчивости замкнутой системы при нарушении идеальных условий, необходимо использовать робастные (грубые) алгоритмы адаптивной настройки. Основная идея обеспечения робастности состоит в замене алгоритмов адаптации "чисто интегрального типа" (1.10) алгоритмами, близкими по своим свойствам к интегральным, но позволяющим избежать неограниченного роста настраиваемых параметров. Робастные алгоритмы адаптации в наиболее общем виде могут быть представлены выражением

(1.11)

где функция настройки в явном виде зависит от благодаря параметрической обратной связи. Отказ от алгоритмов "чисто интегрального типа" ведет к появлению ненулевой установившейся ошибки управления даже при идеальных условиях. Поэтому адаптивная робастная система управления,

обеспечивает выполнение целевого условия (1.2).

Определение 1.2. Система (1.6), (1.7), (1.9) и (1.11) называется адаптивной робастной по отношению к классу и цели управления (1.2), если все сигналы системы являются ограниченными и дополнительно выполняется целевое условие (1.2) для любого вектора и любых начальных условий .

В некоторых случаях не существует постоянного значения вектора настраиваемых параметров , обеспечивающего выполнение поставленной цели управления для всех . Данный факт мотивирует выбор статической обратной связи

(1.12)

Можно сказать, что в известном смысле статическая обратная связь (1.12) (в отличие от интегральной (1.10)) не обладает "памятью". Алгоритмы управления вида (1.9), (1.12) будем называть нелинейными робастными.

Определение 1.3. Система (1.6) (1.7), (1.9) и (1.12) называется нелинейной робастной по отношению к классу и цели управления (1.2), если все сигналы системы являются ограниченными и дополнительно выполняется целевое условие (1.2) для любого вектора и любых начальных условий .

Следует отметить, что в общем случае значение порога Δ зависит от θ и внешних воздействий и как следствие не может быть выбрано произвольным. Однако в некоторых случаях специальный выбор структуры адаптивного робастного управления (1.9) и (1.11) или нелинейного робастного управления (1.9) и (1.12) позволяет обеспечить произвольно малое значение Δ за счет увеличения коэффициента усиления дополнительной обратной связи (1.11) или (1.12).

Различные способы синтеза систем управления неопределенными объектами представлены в виде универсальных методов синтеза. С этой целью рассматривается задача стабилизации применительно к разным классам нелинейных неопределенных систем, подверженных внешним возмущениям. Сначала рассматривается задача управления по состоянию при выполнении условия согласования и синтезируются алгоритмы адаптивного, адаптивного робастного и нелинейного робастного управления, основанные на использовании принципа непосредственной компенсации. Затем исследуется класс нелинейных систем, не удовлетворяющих условию согласования, и вводятся итеративные методы синтеза. Наконец, рассматривается класс неопределенных систем с неизмеряемым вектором состояния и представляются методы синтеза, позволяющие преодолеть структурное ограничение, связанное с высокой относительной степенью объекта управления.

Все методы синтеза, рассматриваемые в этой главе, базируются на использовании второго метода Ляпунова. Это означает, что основная идея данных методов состоит в поиске алгоритма управления (в форме обратной связи по состоянию или выходу) из условия, чтобы производная по времени специально подобранной скалярной функции (функции Ляпунова), вычисленная в силу уравнений замкнутой системы, обладала бы некоторыми желаемыми свойствами. В свою очередь последнее гарантирует достижение заданных свойств устойчивости синтезируемой системы. Альтернативный подход к синтезу систем адаптивного и робастного управления предусматривает использование концепции скоростного градиента

Для того, чтобы в дальнейшем основное внимание сконцентрировать на проблеме компенсации неопределённостей, введем в рассмотрение номинальную (т. е. без каких-либо неопределенностей или возмущений) математическую модель объекта и предположим, что для данной модели традиционными методами найдено стабилизирующее управление. Номинальную модель объекта представим в достаточно общем виде:

(1.13)

где и являются гладкими функциями ( ), – вектор состояния и - сигнал управления. Свойства стабилизирующего управления сформулируем в виде следующего допущения.

Допущение 1.1. Существуют непрерывно дифференцируемая функция , определяющая закон управления в форме обратной связи по состоянию

(1.14)

и гладкая функция (функция Ляпунова) V(х) такие, что

	(1.15)
	(1.16)
	(1.17)

где 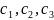и – некоторые положительные константы.

Допущение 1.1 означает, что известен закон управления (1.14), обеспечивающий глобальную экспоненциальную стабилизацию номинальной модели (1.13), а также известна функция Ляпунова V(х), позволяющая доказать данное свойство.

1.2. Управление по состоянию

Предполагается, что вектор состояния неопределенного объекта управления доступен прямым измерениям.

1.2.1 Методы непосредственной компенсации

Рассмотрим неопределенный объект управления вида

(1.18)

где – q-вектор известных функций (регрессор), – неизвестный q-вектор и – n-вектор внешних возмущений. В данной главе везде без потери общности будем считать, что t₀ = 0. Примем следующие гипотезы, касающиеся свойств модели (1.18).

Допущение 1.2. В модели (1.18):

а) вектор-функция 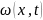является локально липшицевой по х равно-мерно по t;

б) вектор-функция является ограниченной для всех значени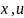й и (например,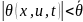 , где - положительная константа);

в) вектор-функция является ограниченной.

Легко видеть, что модель (1.18) удовлетворяет условиям согласования. Если бы вектор-функция θ была известной, то закон управления вида

(1.19)

обеспечил бы полную компенсацию возмущающего влияния θ.

При этом с учетом допущений 1.1 и 1.2, производная по времени функции Ляпунова V(х) замкнутой системы (1.18), (1.19) удовлетворяла бы неравенству

(1.20)

Так как при , то (1.20) означает сходимость x(t) к инвариантному множеству .

Когда вектор-функция θ неизвестна, закон управления (1.19) физически нереализуем. Поэтому в соответствии с принципом непосредственной компенсации вместо (1.19) будем использовать управление

(1.21)

где q-мерный вектор представляет дополнительную обратную связь, обеспечивающую подавление (не обязательно полную компенсацию) неопределенностей θ.