МИНОБРНАУКИ РОССИИ

САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ

ЭЛЕКТРОТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

«ЛЭТИ» ИМ. В.И. УЛЬЯНОВА (ЛЕНИНА)

КАФЕДРА САУ

РЕФЕРАТ

по дисциплине «Нелинейное и адаптивное управление в технических системах»

Тема: Адаптивные системы с переменной структурой, с явной и неявной эталонными моделями. Алгоритмы адаптивной идентификации

Студент гр. 9492		Плотников Д.А.
Преподаватель		Путов В.В.

Санкт-Петербург

2024

1. Адаптивные системы, построенные методом скоростного градиента, с явной эталонной моделью с параметрической, сигнальной и сигнально-параметрической адаптацией

Методика решения задачи адаптивного управления включает несколько этапов. Задано математическое описание объекта управления и внешних воздействий с учетом неизвестных параметров ξ, а также множество Ξ значений этих параметров. Определены спецификация управляющих воздействий и измеряемых выходов объекта. Кроме того, сформулирована цель управления. Процесс синтеза адаптивного регулятора разбивается на последовательные этапы: Этап 1. Выбор «идеального» закона управления; Этап 2. Выбор настраиваемых параметров и цели адаптации; Этап 3. Выбор алгоритма адаптации; Этап 4. Исследование работоспособности адаптивной системы.

1.1 Алгоритмы параметрической адаптации

1. Настройка коэффициентов уравнений состояния. Рассматривается обобщенный настраиваемый объект (ОНО)

(1.1)

где – вектор состояния ОНО; – внешнее командное (задающее) воздействие; – n×n- и n×m-матрицы неизвестных параметров ОНО; – n×n- и n×m-матрицы настраиваемых параметров. Цель управления – совпадение вектора состояния ОНО с вектором состояния (явной) эталонной модели, которая задана уравнением

(1.2)

где – n×n- и n×m-матрицы, описывающие желаемую динамику замкнутой системы ( – гурвицева).

Вывод алгоритма адаптации по методу скоростного градиента. Вводится целевой функционал , где – вектор ошибки; – некоторая n×n-матрица. Вычислим . Тогда

(1.3)

Алгоритм скоростного градиента в дифференциальной форме в данном случае имеет вид

(1.4)

Условие выпуклости выполнено в силу линейности ОНО. Условие достижимости также выполнено при . Матрица должна удовлетворять уравнению Ляпунова для некоторой . Тогда существует некоторое такое, что

Условие роста выполнено для ограниченного , т. е. для ограниченного командного сигнала .

При влиянии возмущений может возникнуть неограниченный рост значений параметров регулятора. Для предотвращения используют регуляризованный алгоритм адаптации. Регуляризованный АСГ с функцией выглядит как

(1.5)

где – некоторые априорные оценки настраиваемых параметров.

Скорость настройки параметров можно увеличить, если использовать АСГ в конечно-дифференциальной форме, которая дает следующие пропорционально-дифференциальные алгоритмы адаптации

(1.6)

Алгоритмы адаптации (1.4), (1.6) обладают идентифицирующими свойствами, т. е. при , если вектор-функция обладает достаточным разнообразием, т. е. модель (1.2) достаточно полно возбуждается входным сигналом.

2. Настройка коэффициентов регулятора. Пусть уравнения объекта есть

(1.7)

где – вектор состояния; – управляющее воздействие. Через обозначим командное (задающее) воздействие.

Целевая функция . Пользуясь схемой скоростного градиента, получаем

(1.8)

Пусть для любых уравнение

(1.9)

разрешимо относительно . Тогда удовлетворяет соотношению

(1.10)

Здесь , т. е. , – линейное подпространство, порожденное столбцами матрицы . Это эквивалентно соотношению

(1.11)

Условие (1.11) называется условием Эрцбергера, условиями адаптируемости, совместимости или точного соответствия модели.

При выполнении этих условий существуют матрица и вектор-функция такие, что , т. е. условие достижимости выполнено при . Матрица может быть найдена из решения уравнения Ляпунова

Возьмем в качестве вектора настраиваемых параметров Скоростной градиент получается в виде

(1.12)

Тогда АСГ в дифференциальной форме записывается как

(1.13)

1.2 Алгоритмы сигнальной адаптации

Данные алгоритмы не предполагают настройки параметров регулятора. Они относятся к АСГ в конечной форме.

Рассматривается задача слежения с явной эталонной моделью (1.2). Уравнения объекта – в виде (1.7).

Используя целевую функцию мы получаем (1.8): . Как и выше, матрица находится из уравнения Ляпунова для некоторой . Используем теперь в качестве вектора настраиваемых параметров непосредственно сигнал управления , и получим алгоритм управления в виде АСГ в конечной форме. Для этого вычислим скоростной градиент . Алгоритм (А.15) принимает (при ) вид

(1.14)

Алгоритмы вида (1.14) обладают высоким быстродействием, но у них отсутствуют идентифицирующие свойства (нет настраиваемых параметров). При изменении параметров объекта в широких пределах целесообразно использовать сигнально-параметрические алгоритмы.

1.3 Алгоритмы сигнально-параметрической адаптации

Рассматривается система, в которую входят ОУ (1.7) и эталонная модель (1.2). Цель управления при .

Функционал качества зададим в виде . Тогда выражение для имеет вид (1.8). Выполнение условий (1.11) обеспечивает единственность решения (1.9) относительно для всех и . Для имеем соотношение

(1.15)

где

При выполнении условий адаптируемости имеются матрица и вектор-функция вида (1.15) такие, что выполняется условие достижимости (А.10). Матрица находится как решение уравнения Ляпунова.

По аналогии с выражением (1.15) выберем алгоритм управления в основном контуре в виде

(1.16)

где 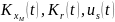– настраиваемые параметры, образующие вектор . Задаваясь матрицей Г в блочно-диагональной форме

получим алгоритм управления

(1.17)

где

2. Адаптивные системы, построенные методом скоростного градиента, с неявной эталонной моделью. Адаптивное управление летательным аппаратом

2.1 Алгоритмы параметрической адаптации

Рассмотрим уравнения ОНО в виде

(2.18)

где , , , – вектор настраиваемых параметров регулятора.

Используем целевой функционал . Применим метод скоростного градиента. Получим, что

Т. к. выражение должно зависеть только от измеряемых переменных, получаем условие для некоторого l-мерного вектора . Предполагая это условие выполненным, запишем АСГ в виде

(2.19)

где матрица коэффициентов усиления .

Для проверки работоспособности алгоритма следует установить только выполнение условия разрешимости. Оно удовлетворяется, если существует вектор такой, что , где . Таким образом, должны существовать матрица и вектор такой, что

(2.20)

Решение этой задачи дает следующая теорема (частотная теорема с обратной связью или теорема о пассификации).

Теорема. Для существования матрицы и вектора , удовлетворяющих (2.3), необходимо и достаточно, чтобы функция была строго-минимально-фазовой.

Здесь – передаточная функция ОУ.

При выполнении указанного условия на , обеспечивается выполнение цели управления при .

2.2 Алгоритмы сигнально-параметрической адаптации

Рассматривается ОУ, выходной сигнал которого непосредственно представляет собой «ошибку» (рассогласование)

(2.21)

где .

Пусть цель управления имеет вид . Возьмем целевую функцию в виде и вспомогательную цель управления при . Такая вспомогательная цель характерна для систем с переменной структурой на скользящих режимах.

Следуя схеме скоростного градиента, получим

(2.22)

Закон управления в основном контуре возьмем в виде

(2.23)

где вектор настраиваемых параметров . Далее получим

(2.24)

Тогда алгоритм адаптивного управления для АСГ в конечной форме (А.15) принимает вид

(2.25)

Отметим, что в системе (2.4), (2.7) возникает скользящий режим на поверхности , следовательно, для достижения цели управления требуется строгая минимально-фазовость передаточной функции

Рассмотрим теперь АСГ в дифференциальной форме. Используем структуру закона управления в виде (А.6) с матрицей

Получим алгоритм управления

(2.26)

где .

Для повышения скорости настройки параметров имеет смысл использовать алгоритм настройки в конечно-дифференциальной форме

(2.27)