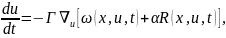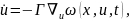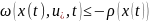1.4. Комбинированные алгоритмы
Выписанные выше алгоритмы можно использовать во всевозможных сочетаниях. Наиболее употребительными из них являются: алгоритм с локально-интегральным функционалом
|
(1.20) |
являющийся АСГ по отношению к функционалу

и АСГ в конечно-дифференциальной форме:
|
(1.21) |
Наиболее общей формой АСГ является
|
(1.22) |
Алгоритм (1.22) становится более наглядным в частном случае, если взять

где
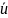 – некоторый постоянный вектор. Тогда
– некоторый постоянный вектор. Тогда
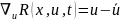 и, меняя местами вторые слагаемые в
(1.22), алгоритм можно представить в виде
и, меняя местами вторые слагаемые в
(1.22), алгоритм можно представить в виде
|
(1.23) |
Соотношение
(1.23) задает преобразование вектора
 в вектор поправки к управлению
в вектор поправки к управлению
 .
Этот закон является линейным и может
быть описан передаточной матрицей
.
Этот закон является линейным и может
быть описан передаточной матрицей

т. е. алгоритму (1.23) соответствует матричное интегро-дифференцирующее звено.
Условия достижения цели управления
Свойства сходимости, позволяющие гарантировать достижение цели управления в системах, построенных методом скоростного градиента. Большая часть результатов относится к общей модели управляемого объекта в виде дифференциальных уравнений состояния
|
(2.24) |
где
 – вектор состояния,
– вектор состояния,
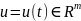 – вектор входов системы. Рассмотрим
условия, при которых алгоритм скоростного
градиента в дифференциальной форме
– вектор входов системы. Рассмотрим
условия, при которых алгоритм скоростного
градиента в дифференциальной форме
|
(2.25) |
где , обеспечивает достижение цели управления, заданной при помощи локального целевого функционала.
Теорема 2.1. Пусть выполнены следующие предположения.
А1.
Функции
 и
и
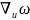 непрерывны по
непрерывны по
 ,
,
 ,
кусочно непрерывны по
и локально ограничены равномерно по
,
т. е. для любого
,
кусочно непрерывны по
и локально ограничены равномерно по
,
т. е. для любого
 существует
существует
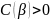 такое, что неравенство
такое, что неравенство

имеет место при
 ,
,
 .
.
А2.
Функция
неотрицательна, равномерно непрерывна
в любом множестве вида
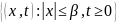 и радиально неограничена:
и радиально неограничена:
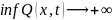 при
при

А3. Функция выпукла по , т. е. неравенство
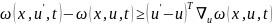
выполнено для всех
 .
.
А4.
Существуют постоянный вектор
 и
и
 -функция
-функция
 такая, что неравенство
такая, что неравенство

выполнено для всех
 .
.
Тогда
все решения
 системы (2.1), (2.2) ограничены (т. е. система
устойчива по Лагранжу) и цель
системы (2.1), (2.2) ограничены (т. е. система
устойчива по Лагранжу) и цель
|
(2.26) |
достигается для всех
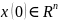 .
.
Теорема 2.2. Пусть выполнены условия А1–А3 теоремы 2.1, а также следующие предположения.
А4’.
Существуют постоянный вектор
и неотрицательная непрерывная скалярная
функция
 такие, что для любого решения
такие, что для любого решения
 системы (2.1) при
системы (2.1) при
 неравенство
неравенство
|
(2.27) |
выполняется при всех .
А5.
Для любых
 существует решение
существует решение
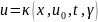 уравнения
уравнения
 ,
причем функция
,
причем функция
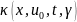 локально ограничена равномерно по
.
локально ограничена равномерно по
.
Тогда все решения системы (2.1), (1.21) ограничены и

Более сильное утверждение имеет место, если алгоритм скоростного градиента в конечной форме удовлетворяет условию псевдоградиентности в усиленной форме. Рассмотрим систему (2.1) вместе с алгоритмом управления
|
(2.28) |
где .
Теорема 2.3. Пусть выполнены условия А1–А3 теоремы 2.1, а также следующие предположения.
А4’’.
Существует локально ограниченная
равномерно по
вектор-функция
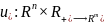 скалярная
-функция
скалярная
-функция
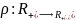 такая, что для любого решения
такая, что для любого решения
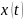 системы (2.1) при
системы (2.1) при
 выполняется следующее неравенство:
выполняется следующее неравенство:

А5. Для любых существует решение уравнения , причем функция локально ограничена равномерно по .
А6.
Существуют числа
и
 такие, что
такие, что

Тогда все решения системы (2.1), (2.5) ограничены и
1)
если
 ,
то для любого
,
то для любого
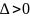 существует
существует
 такое, что следующая цель управления
достигается при
такое, что следующая цель управления
достигается при
 :
:
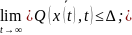
2)
если
 ,
то существует
,
то существует
 такое, что следующая цель управления
достигается при
:
такое, что следующая цель управления
достигается при
:

Перейдем к рассмотрению случая, когда цель управления задана при помощи интегрального целевого функционала

Соответствующий алгоритм скоростного градиента в дифференциальной форме выглядит так:
|
(2.29) |
Нижеследующая теорема устанавливает условия достижения цели в системе с алгоритмом (2.6).
Теорема 2.4. Рассмотрим систему (2.1), (2.6) при следующих предположениях.
А1.
Функции
 непрерывна по
,
кусочно-непрерывны по
и локально ограничены равномерно по
.
непрерывна по
,
кусочно-непрерывны по
и локально ограничены равномерно по
.
А2. Для всех величины неотрицательны.
А3.
Функция
 выпукла по
.
выпукла по
.
А4’’’’.
Существуют постоянный вектор
и скалярная функция
 со свойствами
со свойствами

такие, что для любого решения системы (2.1) при выполняется неравенство
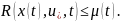
Тогда:
1)
достигается цель управления
 ,
где
,
где

2)
любое ограниченное решение системы
(2.1), (2.6) удовлетворяет соотношению