МИНОБРНАУКИ РОССИИ
САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ
ЭЛЕКТРОТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
«ЛЭТИ» ИМ. В.И. УЛЬЯНОВА (ЛЕНИНА)
КАФЕДРА САУ
РЕФЕРАТ
по дисциплине «Нелинейное и адаптивное управление в технических системах»
Тема: Метод скоростного градиента
Студент гр. ХХХХХХХХХ |
|
ХХХХХХХХХ |
Преподаватель |
|
ХХХХХХХХХ |
Санкт-Петербург
2024
Описывается общий подход к синтезу нелинейных систем управления – метод скоростного градиента. Метод основан на использовании функций Ляпунова и требует задания цели управления как уменьшения значений некоторой скалярной целевой функции до заданной величины.
Построение алгоритмов скоростного градиента
Исходными данными для синтеза алгоритма управления являются: уравнение объекта управления (далее «объект») и цель управления. Пусть объект задан уравнением
|
(1.1) |
где
 – вектор состояния объекта,
– вектор состояния объекта,
 – вектор управления, вектор-функция
– вектор управления, вектор-функция
 определена при всех
определена при всех
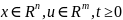 ,
кусочно-непрерывна по
,
кусочно-непрерывна по
 и непрерывно дифференцируема по
и непрерывно дифференцируема по

Цель управления (ЦУ) задается в виде
|
(1.2) |
где
 – целевой функционал (постоянные
– целевой функционал (постоянные
 ,
,
 могут быть заданы или нет в зависимости
от конкретной задачи). Различают два
типа целевых функционалов: локальный
и интегральный. Локальным называется
функционал вида
могут быть заданы или нет в зависимости
от конкретной задачи). Различают два
типа целевых функционалов: локальный
и интегральный. Локальным называется
функционал вида
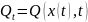 ,
где
,
где
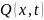 – скалярная функция
– скалярная функция
 переменных. Функционал вида
переменных. Функционал вида
|
|
где
 – скалярная функция
– скалярная функция
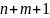 переменных называется интегральным.
переменных называется интегральным.
Ставится задача: определить алгоритм управления
|
(1.3) |
так, чтобы в системе (1.1), (1.3) достигалась
ЦУ (1.2) и все её траектории оставались
ограниченными при
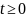 .
.
Формулированная
задача обща и включает как частные
случаи различные типы задач управления
и адаптации. Например, в качестве ЦУ
(1.2) может фигурировать как исходная
цель управления, так и некоторая
вспомогательная цель, выражающая
требования к синтезируемой системе.
Уравнение (1.1) также может относиться к
различным системам. Более того, в одной
и той же системе управления модель (1.1)
может использоваться для описания
различных частей системы так, что
переменные
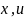 могут иметь различный смысл. Введение
такого унифицированного описания
позволяет единообразно ставить и решать
задачи синтеза как основного контура,
так и контура адаптации в адаптивных
системах.
могут иметь различный смысл. Введение
такого унифицированного описания
позволяет единообразно ставить и решать
задачи синтеза как основного контура,
так и контура адаптации в адаптивных
системах.
Пример
1.1. Пусть
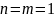 ,
а объект управления описывается скалярным
уравнением
,
а объект управления описывается скалярным
уравнением
|
(1.4) |
где
 – искомый входной сигнал. Описание
(1.4) эквивалентно заданию передаточной
функции
– искомый входной сигнал. Описание
(1.4) эквивалентно заданию передаточной
функции
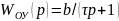 и приводится к виду (1.1) при
и приводится к виду (1.1) при

Если же к объекту подключить линейный регулятор
|
(1.5) |
где
 – задающее воздействие (уставка,
командный сигнал), и ставить задачу
определения коэффициента усиления
– задающее воздействие (уставка,
командный сигнал), и ставить задачу
определения коэффициента усиления
 ,
то уравнение (1.1) будет выглядеть иначе.
Уравнение замкнутой системы (уравнение
основного контура) получается при
подстановке (1.5) в (1.4) и имеет вид
,
то уравнение (1.1) будет выглядеть иначе.
Уравнение замкнутой системы (уравнение
основного контура) получается при
подстановке (1.5) в (1.4) и имеет вид
|
(1.6) |
Входом
в (1.6) следует считать величину
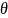 .
После переобозначения
.
После переобозначения
 уравнение (1.6) приводится к форме (1.1),
однако будет описывать уже не линейную,
а билинейную систему, для которой задача
синтеза управления будет соответствовать
задаче синтеза контура адаптации для
исходного объекта (1.4).
уравнение (1.6) приводится к форме (1.1),
однако будет описывать уже не линейную,
а билинейную систему, для которой задача
синтеза управления будет соответствовать
задаче синтеза контура адаптации для
исходного объекта (1.4).
Заметим, что как (1.4), так и (1.6) описывают объекты, линейные по входам. Этот класс объектов играет важную роль в задачах синтеза нелинейных и адаптивных систем. В общем случае уравнение линейной по входам системы будем записывать в виде
|
(1.7) |
где
 – n-вектор,
– n-вектор,
 – n×m-матрица.
Уравнение (1.7) можно переписать также в
виде
– n×m-матрица.
Уравнение (1.7) можно переписать также в
виде
|
(1.8) |
где
 – компоненты вектора
;
– компоненты вектора
;
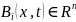 – столбцы матрицы
.
– столбцы матрицы
.


 или
или