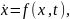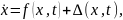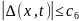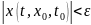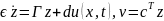4. Грубость свойств динамических систем

Для прикладных задач теории управления наибольший интерес представляет вопрос о сохранении некоторых желаемых свойств (и прежде всего - свойств устойчивости) динамических систем при вариациях их математических моделей. Такая трактовка грубости была дана Н.Н. Красовским в IV главе его книги. Ниже вводится понятие грубости свойств динамических систем в смысле определения Н.Н. Красовского и показывается, как для ее исследования может быть использован аппарат функции Ляпунова.

В последнее время часто вместо термина "грубость" используется термин робастность. Обычно, говоря о робастности, предполагают знание количественных оценок допустимых вариаций математической модели. В этом смысле "грубость" может трактоваться как "локальная робастность". Отметим, что термины "грубый и робастный" используются также по отношению к алгоритмам управления и замкнутым системам при условии, что оговорены класс номинальных моделей систем, класс допустимых вариаций и указано свойство системы, сохраняющееся при данных вариациях.

Рассматривается номинальная система

(4.32)

и возмущенную систему вида

(4.33)

где слагаемое 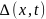определяет класс вариаций номинальной модели. При различных предположениях о вариациях 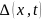получаются различные типы грубости. Начнем с так называемых мультипликативных возмущений, определяемых неравенством

(4.34)

где 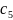– некоторое положительное число.

Свойство устойчивости системы (4.1) называется грубым по отношению к мультипликативным возмущениям, если может быть указано число 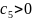такое, что данное свойство устойчивости справедливо также для системы (4.2) при любых , удовлетворяющих условию (4.3).

Очевидно, что свойство устойчивости по Ляпунову не является грубым по отношению к мультипликативным возмущениям.

Теперь перейдем к другому классу возмущений, которые не обязательно исчезают при 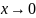, но удовлетворяют условию ограниченности

(4.35)

для любых и . Такой вид вариаций будем называть аддитивными возмущениями (в теории дифференциальных уравнений возмущения (4.4) иногда называются постоянно действующими возмущениями).

Свойство устойчивости системы (4.1) называется грубым по отношению к аддитивным возмущениям, если для любого числа 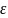могут быть найдены положительные числа 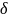и 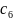такие, что неравенство

(4.36)

выполняются на всех траектория системы, начинающихся в области 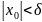при любых вариациях модели , которые удовлетворяют неравенству (4.5).

Свойство неравномерной асимптотической устойчивости не является грубым по отношению к аддитивным возмущениям.

Наконец, рассмотрим случай структурных возмущений, вызванных наличием так называемой паразитной динамики. Пусть номинальная модель (4.1) представима в виде

(4.37)

где 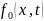и 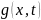– n-мерные вектор функции, а 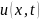– скалярная функция. Представление (4.6) мотивировано задачами синтеза систем управления, где функция интерпретируется в качестве закона (алгоритма) управления. Возмущенную модель определим в виде

	(4.38)
	(4.39)

где уравнение (4.8) описывает паразитную динамику, 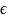– малый постоянный параметр, – вектор состояния модели (4.8), 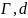и – матрица и векторы постоянных коэффициентов соответствующих размерностей, а тройка ( ) является минимальной реализацией передаточной функции 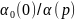, где 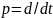– оператор дифференцирования. В этом случае .

При обращении є в ноль изменяется структура модели (4.7)-(4.8), что мотивирует использование термина структурные возмущения. Так как при этом меняется порядок системы, то такие возмущения называются сингулярными, а сама система (4.7)-(4.8) - сингулярно возмущенной. Очевидно, что изменение параметра є без обращения в ноль будет относиться к классу параметрических возмущений.

Отметим, что в общем случае для описания паразитной динамики может быть выбрана нелинейная экспоненциально устойчивая модель. Однако для простоты изложения ограничимся случаем линейной модели (2.58).

Свойство устойчивости системы (4.6) называется грубым по отношению к паразитной динамике, если при заданной тройке ( ) можно указать такое 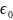, что данное свойство устойчивости справедливо для системы (4.7)-(4.8) для любых и, по крайней мере, ограниченного множества 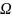начальных условий .
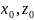