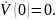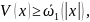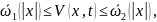Метод функций Ляпунова
Одним из наиболее распространенных средств анализа и синтеза сложных систем управления является второй (или прямой) метод Ляпунова.
Рассматриваются
динамические системы вида (1.1), определенные
на открытом множестве
,
где
 ,
,
а также стационарные системы (1.3),
определенные на множестве
.
Пусть правые части систем таковы, что
удовлетворяются условия существования
и единственности решений, а сами решения
(1.2) определены на полубесконечном
интервале времени
,
,
а также стационарные системы (1.3),
определенные на множестве
.
Пусть правые части систем таковы, что
удовлетворяются условия существования
и единственности решений, а сами решения
(1.2) определены на полубесконечном
интервале времени
 .
Пусть выделено некоторое решение
.
Пусть выделено некоторое решение
 системы (1.1) – так называемое невозмущенное
решение. Замена переменных
системы (1.1) – так называемое невозмущенное
решение. Замена переменных
 приводит систему (1.1) к виду
приводит систему (1.1) к виду
 ,
где
,
где
|
(3.19) |
В
качестве функций Ляпунова рассматриваются
непрерывно дифференцируемые скалярные
функции
 или
или
 ,
которые в некоторой окрестности положения
равновесия
,
которые в некоторой окрестности положения
равновесия
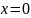 являются положительно определенными.
являются положительно определенными.
Достаточные условия устойчивости по Ляпунову положения равновесия системы (1.1) определяются следующей теоремой, доказанной А.М. Ляпуновым.
Теорема 3.1 (1-я теорема Ляпунова). Равновесное состояние системы (1.1) устойчиво, если в некоторой окрестности точки существует функция Ляпунова , производная которой является неположительной функцией, т. е. в указанной окрестности и для любых t E Т выполняется неравенство выполняется неравенство
|
(3.20) |
Теорема 3.2. Равновесное состояние системы (1.1) равномерно устойчиво, если в некоторой окрестности точки существует функция Ляпунова такая, что
|
(3.21) |
равномерно по и
|
(3.22) |
Равновесное
состояние
системы (1.3) асимптотически устойчиво,
если в некоторой окрестности точки
существует функция Ляпунова
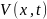 ,
такая, что ее производная является
отрицательно определенной функцией,
т. е.
,
такая, что ее производная является
отрицательно определенной функцией,
т. е.
|
(3.23) |
Теорема 3.3 (2-я теорема Ляпунова). Равновесное состояние системы (1.1) асимптотически устойчиво, если в некоторой окрестности точки существует функция Ляпунова такая, что
|
(3.24) |
а её производная является отрицательно определенной, т. е.
|
(3.25) |
где
 ,
,
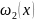 ,
,
 – положительно определенные функции.
– положительно определенные функции.
Поскольку глобально устойчивая система может обладать лишь одним состоянием равновесия, то в формулировках (если это не вызывает недоразумений) его иногда не указывают. Для стационарных систем основные результаты получены Е.А. Барбашиным и Н.Н. Красовским.
Теорема
3.4.а (теорема Барбашина-Красовского).
Пусть
.
Система (1.3) глобально асимптотически
устойчива в точке
,
если существует функция Ляпунова
 ,
определенная на всем множестве
такая, что
,
определенная на всем множестве
такая, что
1)
для всех

|
(3.26) |
где
 –
–
 -функция;
-функция;
2)
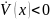 при
,
при
,
В сложных случаях можно использовать более общий вариант этой теоремы.
Теорема 3.4.б (теорема Барбашина-Красовского). Пусть . Система (1.3) глобально асимптотически устойчива в точке , если существует функция Ляпунова , определенная на все множестве , такая, что
1) для всех
|
(3.27) |
2)
 ,
а множество
,
а множество
 не содержит целых траекторий системы
(1.3) за исключением
не содержит целых траекторий системы
(1.3) за исключением
 .
.
Следующая теорема касается свойств нелинейных систем общего вида (1.1).
Теорема 3.5. Пусть . Система (1.1) глобально равномерно асимптотически устойчива в точке , если существует функция Ляпунова , определенная на всем множестве , , такая, что
1) для всех и
|
(3.28) |
2)
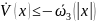 .
.
Теорема
3.5 (Н.Н. Красовский). Пусть
.
Система (1.1) с непрерывно дифференцируемой
правой частью (т. е.
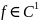 )
глобально экспоненциально устойчива
в точке
тогда и только тогда, когда существует
функция Ляпунова
,
удовлетворяющая условиям
)
глобально экспоненциально устойчива
в точке
тогда и только тогда, когда существует
функция Ляпунова
,
удовлетворяющая условиям
|
(3.29) |
|
(3.30) |
|
(3.31) |
где
 – положительные константы.
– положительные константы.


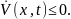
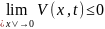
 при
при
 ,
,