МИНОБРНАУКИ РОССИИ
САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ
ЭЛЕКТРОТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
«ЛЭТИ» ИМ. В.И. УЛЬЯНОВА (ЛЕНИНА)
КАФЕДРА САУ
РЕФЕРАТ
по дисциплине «Нелинейное и адаптивное управление в технических системах»
Тема: Свойства нелинейных систем и проблемы устойчивости
Студент гр. ХХХХХХХХХ |
|
ХХХХХХХХХ |
Преподаватель |
|
ХХХХХХХХХ |
Санкт-Петербург
2024
СОДЕРЖАНИЕ
1. Свойства решений дифференциальных уравнений 3
2. Равновесные состояния и устойчивость 7
3. Метод функций Ляпунова 10
4. Грубость свойств динамических систем 13
Реферат содержит краткое изложение некоторых понятий теории обыкновенных дифференциальных уравнений (далее ДУ), наиболее часто использующихся при анализе свойств нелинейных динамических систем, а также ключевые положения современной теории устойчивости, описываемые системами обыкновенных ДУ.
Свойства решений дифференциальных уравнений
Рассматривается нелинейная динамическая система, описываемая обыкновенным ДУ вида:
|
(1.1) |
где
 – n-мерный вектор состояния
системы,
– n-мерный вектор состояния
системы,
 – время. Полагается, что
– время. Полагается, что
 ,
где
,
где
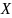 и
и
 – открытые множества (множества, каждый
элемент которого входит в его окрестности)
соответствующих пространств,
– открытые множества (множества, каждый
элемент которого входит в его окрестности)
соответствующих пространств,
 – n-мерная вектор-функция,
определенная на множестве
– n-мерная вектор-функция,
определенная на множестве
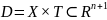 .
.
Решением
ДУ (1.1) с начальными условиями
 ,
,
 называется функция
называется функция
|
(1.2) |
определенная на некотором интервале
времени
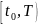 ,
где
,
где
 ,
,
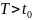 ,
дифференцируемая по
и удовлетворяющая условиям:
,
дифференцируемая по
и удовлетворяющая условиям:
1) |
|
2) |
|
3) |
|
Первое
условие гласит, при времени
решение ДУ сводится к
 .
Второе условие –
.
Второе условие –
 принадлежит декартовому произведению
двух множеств.
принадлежит декартовому произведению
двух множеств.
Для
любого момента времени
 функция
функция
 определяет нестационарное (т. е.
параметризованное временем
)
векторное поле на множестве
,
т. е. отображение точек
определяет нестационарное (т. е.
параметризованное временем
)
векторное поле на множестве
,
т. е. отображение точек
 в элементы (векторы скорости) пространства
в элементы (векторы скорости) пространства
 .
Отображение (1.2)
.
Отображение (1.2)
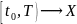 ,
соответствующее решению ДУ (1.1) с
начальными условиями
,
соответствующее решению ДУ (1.1) с
начальными условиями
 и
,
называется интегральной кривой или
линией потока векторного поля
и
,
называется интегральной кривой или
линией потока векторного поля
 .
Данная терминология часто используется
самой кривой как динамической системы
(1.1). Множество интегральных кривых,
соответствующих фиксированному моменту
и различным значениям
.
Данная терминология часто используется
самой кривой как динамической системы
(1.1). Множество интегральных кривых,
соответствующих фиксированному моменту
и различным значениям
 ,
образуют поток векторного поля
на множестве
.
В произвольной точке
вектор-функция
,
образуют поток векторного поля
на множестве
.
В произвольной точке
вектор-функция
 в момент времени
является касательным к интегральной
кривой
в момент времени
является касательным к интегральной
кривой

При
условии, что
является гладкой (дифференцируемая
бесконечное число раз) во всех точках
множества
 ,
система (1.1) называется гладкой динамической
системой. Её решения (интегральные
кривые) и траектории в области
также оказываются гладкими.
,
система (1.1) называется гладкой динамической
системой. Её решения (интегральные
кривые) и траектории в области
также оказываются гладкими.
Частный случай системы (1.1) – стационарная динамическая система
|
(1.3) |
где вектор функция
не зависит от времени и определяет
стационарное векторное поле на
.
Можно положить
 ,
,
 и записать решение уравнения (1.3) в виде:
и записать решение уравнения (1.3) в виде:
|
(1.4) |
Одним
из важнейших вопросов, затрагивающем
фундаментальные свойства нелинейных
динамических систем (ДУ (1.1) и (1.3)),
относятся вопросы существования,
единственности и продолжимости их
решений. Принято полагать, что по
некоторым «физическим соображениям»
для любых начальных условий
 найдется интегральная кривая (1.2), которая
единственна и определена на полубесконечном
интервале времени
найдется интегральная кривая (1.2), которая
единственна и определена на полубесконечном
интервале времени
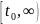 .
.
Достаточные условия существования решений нелинейного ДУ (1.1) даются теоремой Пеано.
Теорема
1.1. Пусть
 и
и
 – открытые множества. Если
непрерывна в области
– открытые множества. Если
непрерывна в области
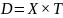 (объединение подмножеств,
является открытым множеством), то для
любых начальных условий
(объединение подмножеств,
является открытым множеством), то для
любых начальных условий
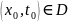 существует решение
существует решение
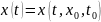 ,
определенное на некотором интервале
,
определенное на некотором интервале
 ,
,
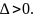
Данная теорема предлагает лишь достаточные условия существования, которые в ряде случаев оказываются излишне жесткими. С другой стороны, выполнение её условий еще не гарантирует единственности решений (1.2).
Условие
единственности решений обычно
формулируется как требование достаточной
гладкости функции
,
например в форме условия Липшица. Функция
называется липшецовой по
в замкнутой области
 ,
если существует константа
,
если существует константа
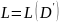 такая, что выполняется неравенство
такая, что выполняется неравенство
|
(1.5) |
для любых пар
 ,
,
 .
Функция
называется локально липшецовой по
в открытой области
,
если она липшицева в любой замкнутой
области
.
Функция
называется локально липшецовой по
в открытой области
,
если она липшицева в любой замкнутой
области
 .
.
Непродолжаемое
решение ДУ (1.1) – решение ДУ
 ,
определенное либо на полубесконечном
интервале
,
определенное либо на полубесконечном
интервале
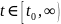 ,
либо на таком конечном интервале
,
что функция
,
либо на таком конечном интервале
,
что функция
 ,
заданная на промежутке
,
заданная на промежутке
 для любых значений
для любых значений
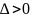 ,
не является решением уравнения (1.1).
,
не является решением уравнения (1.1).
Условие единственности непродолжаемого решения устанавливается следующей теоремой.
Теорема
1.2 (предложена академиком Тихоновым).
Пусть
и
– открытые множества. Если фукнция
непрерывна и локально липшицева по
в области
,
то для любых начальных условий
,
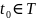 система (1.1) имеет единственное
непродолжаемое решение (1.2).
система (1.1) имеет единственное
непродолжаемое решение (1.2).
Для
сужения класса систем и допустимых
функций
рассматривается система (1.1), определенная
на открытом множестве
,
полагая, что
 .
.
Система
(1.1) (векторное поле
),
называется полной на множестве
,
если для всех
и
её решения (1.2) определены на полубесконечном
интервале
и
 .
.
Простые достаточные условия существования решений и полноты системы в пространстве устанавливаются следующей теоремой.
Теорема
1.3 (предложена академиком В. В. Зубовым).
Пусть
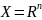 и
.
Если в области
и
.
Если в области
 функция
непрерывна, локально липшицева по
и ограничена, т. е. для всех
найдется число
функция
непрерывна, локально липшицева по
и ограничена, т. е. для всех
найдется число
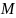 такое, что
такое, что
|
(1.6) |
то для любых начальных условий система (1.1) имеет единственное непродолжаемое решение (1.2), определенное на интервале и, следовательно, является полной в .
Менее жесткие условия предусмотрены в следующей теореме.
Теорема
1.4 (профессор Демидович Б. П.). Пусть
и
.
Если функция
непрерывна и глобально липшицева по
равномерно по
(не зависит от выбора по
),
то для любых начальных условий
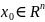 и
система (1.1) имеет единственное
непродолжаемое решение (1.2) и является
полной в
.
и
система (1.1) имеет единственное
непродолжаемое решение (1.2) и является
полной в
.
Более широкие достаточные условия полноты системы можно получить, переходя от неравенств для норм к неравенствам для скорости изменения некоторых функций вдоль решений системы, что позволяет строить соответствующие мажоранты решений.