Пр.4

МИНОБРНАУКИ РОССИИ

САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ

ЭЛЕКТРОТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

«ЛЭТИ» ИМ. В.И. УЛЬЯНОВА (ЛЕНИНА)

КАФЕДРА САУ

ОТЧЕТ

по практической работе №4

по дисциплине «Акустическое проектирование электроэнергетического оборудования»

Тема: Расчет переменных радиальных электромагнитных сил в АД при несимметрии и несинусоидальном напряжении в СЭЭС

Студент гр. ХХХХХХХХ		ХХХХХХХХ
Преподаватель		ХХХХХХХХ

Санкт-Петербург

2024

Постановка задачи.

Радиальные силы, создаваемые основными магнитными полями, вызывают вибрацию на частоте с порядком . Такие вибрации сильно проявляются в крупных АД с числом полюсов . Силовые волны, возникающие при взаимодействии высших гармоник, вызывают наиболее интенсивные вибрацию и шум при низких порядках Значение и распределение радиальных магнитных сил в воздушном зазоре определяются магнитной индукцией, расчет которой требует достаточно подробных характеристик обмоток статора и ротора. Некоторые харак-теристики достаточно стабильны и могут быть использованы для расчета. Радиальная электромагнитная сила, действующая на единицу площади (приведенная к среднему радиусу спинки статора), определяется формулой для амплитудных значений:

где – магнитная постоянная; – магнитная индукция в воздушном зазоре. Обычно принимают для амплитуды силовых волн, возбуждаемых первыми пазовыми гармониками. Если знать число пазов на полюс и фазу , можно воспользоваться приближенным выражением . При этом амплитуда силовой волны составляет 0,5…1 Н/см². В данном расчете необходимо определить влияние качеств электроэнергии на шум и вибрации, поэтому следует рассчитать амплитуды магнитного поля, возбуждаемого системой токов прямой и обратной последовательностей q-й гармоники тока.

Исходные данные.

Амплитуда основной волны магнитной индукции прямой и обратной последовательностей при несимметрии напряжения , , Тл; частота напряжения питания , рад/с; число пар полюсов ; амплитуда основной волны магнитной индукции, создаваемой q-й гармоники тока . В том случае, когда параметры магнитной индукции не заданы, необходимо иметь данные об обмотке статора и параметры схемы замещения. Кроме того, должны быть заданы: число эффективных проводников в фазе обмотки статора ω; обмоточный коэффициент ; коэффициент Картера ; величина возду-шного зазора δ, мм; амплитуды намагничивания тока из схемы замещения АД для напряжения прямой и обратной последовательностей , или данные для их расчета.

Данные для расчета приведены в таблице 1.

Таблица 1 — Исходные данные

Вариант
	А
1	10	1,0	5,0	3,0	2,0	1,0	0,5

; ; мм; ; .

Требуется найти.

Амплитуды силовых волн , ; частоты силовых волн , ; порядки силовых волн , .

Алгоритм расчета.

По направлению силы электромагнитного происхождения в АД делятся на аксиальные силы, вызывающие смещение ротора по отношению к сердечнику статора, тангенциальные силы, создающие вращающий момент и вызывающие вибрации обмоток и радиальные, вызывающие в широком спектре частот изгибные колебания корпуса.

Наибольший вклад вносят радиальные вибровозмущающие силы, удельное значение которой можно определить по формуле

где – мгновенное значение магнитной индукции в воздушном зазоре в точке с угловой координатой в момент времени .

Пусть индукция магнитного поля прямой последовательности (основная гармоника) описывается гармоническим уравнением

где – амплитуда индукции магнитного поля основной гармоники; – число пар полюсов АД; – частота прямой последовательности; – некоторое смещение по фазе.

Тогда удельная радиальная вибровозмущающая сила будет равна

Используя формулу понижения порядка, получим выражение

Из полученного выражения видно, вторая слагаемая вызывает вибрации удвоенной частоты и пространственного порядка . При этом амплитуда радиальной вибровозмущающей силы равна

Рассмотрим магнитное поле, состоящее из двух гармоник, или, иначе говоря, взаимодействие высших гармоник (прямая и обратная последователь-ности). Пусть магнитное поле описывается уравнением

Тогда радиальная вибровозмущающая сила будет равна

Используем формулу произведения косинусов и формулу понижения порядка:

Тогда

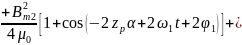
Из последнего слагаемого видно, что амплитуда вибровозмущающей силы взаимодействия полей высших гармоник может быть определена выражением

где амплитуда волны магнитной индукции определяется формулой

Алгоритм определения частоты поля взаимодействия двух волн и их пространственного порядка. Рассмотрим пример взаимодействия первой и третьей гармоники.

Тогда радиальная вибровозмущающая сила (рассматриваем только произведение)

В данном случае для АД характерны вибрации с частотой и с пространственным порядком и 0 соответственно.

Решение.

Несимметрия напряжения.

С помощью заданных значений соответствующих токов определим амплитуды основной волны магнитной индукции прямой и обратной последовательностей:

Амплитуды силовых волн радиальных электромагнитных сил:

Несинусоидальность напряжения.

Рассмотрим поле взаимодействия 1–5, 1–7, 5–7 и 11–13 гармоник.

Пусть

Тогда амплитуды магнитной индукции:

Определим амплитуды радиальных вибровозмущающих сил:

Определим частоты вибраций и пространственные порядки при взаимодействующих гармониках:

Выводы.

Были рассчитаны параметры, характеризующие радиальные вибровозмущающие силы при несимметрии и несинусоидальности напряжения в АД, а именно амплитуды волны магнитной индукции, амплитуды силовых волн, угловые частоты силовых волн и пространственные порядки силовых волн.

Очевидно, что при взаимодействии двух гармоник i и j (из 1, 5, 7, 11 и 13) вибровозмущающая сила будет состоять из двух гармоник с частотами и , при этом пространственные порядки силовых волн будут оставаться неизменными и равными и соответственно. На этой основе составлена таблица 2, показывающая зависимость частот вибровозмущающей силы при взаимодействии двух гармоник от порядка этих гармоник.

Таблица 2 — Частоты вибровозмущающей силы

Порядок	1	5	7	11	13
1		и	и	и	и
5	и		и	и	и
7	и	и		и	и
11	и	и	и		и
13	и	и	и	и