Пр.3

МИНОБРНАУКИ РОССИИ

САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ

ЭЛЕКТРОТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

«ЛЭТИ» ИМ. В.И. УЛЬЯНОВА (ЛЕНИНА)

КАФЕДРА САУ

ОТЧЕТ

по практической работе №3

по дисциплине «Акустическое проектирование электроэнергетического оборудования»

Тема: Расчет амплитуды пульсирующего момента в АД при несинусоидальном напряжении в СЭЭС

Студент гр. ХХХХХХХХ		ХХХХХХХХ
Преподаватель		ХХХХХХХХ

Санкт-Петербург

2024

Постановка задачи.

Широкое внедрение статических преобразователей частоты для регулируемого по частоте электропривода переменного тока, широтно-импульсных регуляторов частоты, других нелинейных потребителей приводит к появлению высших гармоник напряжения в сетях переменного тока. Эти составляющие оказывают значительное влияние на вибрацию АД. Точность расчета пульсирующего момента во многом определяется уровнем исходных данных, в частности, комплексными амплитудами гармонических составляющих фазного напряжения. Здесь рассмотрим только упрощенный расчет при условии, что в СЭЭС фазовый сдвиг между двумя соседними высшими гармониками в каждой паре (5 – 7, 11 – 13…) незначителен и взаимное влияние высших гармоник между собой можно не учитывать.

Исходные данные.

Гармонические составляющие фазного напряжения питания, В: , , , , , , ; индуктивные сопротивления упрощенной схемы замещения АД для высших гармоник или данные для их расчета, , , Ом; частота напряжения питания , Гц; число пар полюсов .

Данные для расчета приведены в таблице 1.

Таблица 1 — Исходные данные

Вариант
	В								Гц				Ом
2	220	38	27	18	15	12	7	50		2		2,7		3,5

Требуется найти.

Амплитуды пульсирующих моментов при несинусоидальности напряжения питания , Н∙м, на соответствующих частотах:

Алгоритм расчета.

Известно, что взаимодействия высших гармоник вызывает наибольшие пульсации момента. Поскольку активное сопротивление в схеме замещения асинхронного двигателя не зависит от частоты, то его можно не учитывать, т.к. рассматриваются высшие гармоники (частоты, в разы превышающие основную частоту). Поэтому расчет будет производиться по схеме замещения, которая приведена на рисунке 1.

Рисунок 1 — Схема замещения АД для расчета амплитуды пульсирующего момента при несинусоидальном напряжении

В данной схеме индуктивное сопротивление намагничивания не учитывается, поскольку в обратном случае, при составлении общего сопротивления мы имеем:

Известно, что при несинусоидальности напряжения в СЭЭС момент будет пульсировать с частотой взаимодействия высших гармоник, то есть с частотами .

Приближенно амплитуду пульсирующего момента можно рассчитать по формуле

где , – комплексное сопротивление упрощенной схемы замещения АД (рис. 1) для высших гармоник и соответственно, то есть для каждой из пар высших гармоник на средней частоте.

Решение.

Используя формулу амплитуды пульсирующего момента для 5 и 7 гармоники имеем:

Поскольку мы пренебрегаем активным сопротивлением, можно положить, что . Тогда, для 5 и 7 гармоники имеем:

Общее сопротивление схемы замещения:

Тогда:

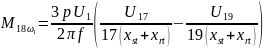
Листинг и результаты вычислений приведены ниже:

u1 = 220;

u5 = 38; u7 = 27;

u11 = 18; u13 = 15;

u17 = 12; u19 = 7;

f = 50; p = 2;

x_st = 2.7; x_rt = 3.5;

Z = x_st + x_rt;

M_6 = (3*p*u1/(2*pi*f))*((u5/(5*Z)) - (u7/(7*Z)))

M_12 = (3*p*u1/(2*pi*f))*((u11/(11*Z)) - (u13/(13*Z)))

M_18 = (3*p*u1/(2*pi*f))*((u17/(17*Z)) - (u19/(19*Z)))

M_6 =

2.5365

M_12 =

0.3270

M_18 =

0.2287

Выводы.

В данной работе были рассчитаны амплитудные значения пульсирующего момента при несинусоидальности напряжения в СЭЭС, которые дают количественную оценку влияния несинусоидальности сети на вибрацию АД. Внедрение преобразователей частоты, других нелинейных потребителей приводит к появлению высших гармоник напряжения в сетях переменного тока. Эти составляющие оказывают значительное влияние на вибрацию АД.

В результате выполнения предложенного метода приближенного расчета амплитуд пульсирующих на разных частотах моментов были получены следующие значения:

Из этого можно сделать вывод о том, что при несинусоидальности напряжения в сети наибольшее влияние на АД оказывают гармоники низшего порядка.