Лаб. 7 ФЛП

Лабораторная работа 7

%1

% Проверяем, что N — целое и положительное

%triangle(N, _) :-

% \+ integer(N), !, fail.

%triangle(N, _) :-

% N =< 0, !, fail.

% База рекурсии

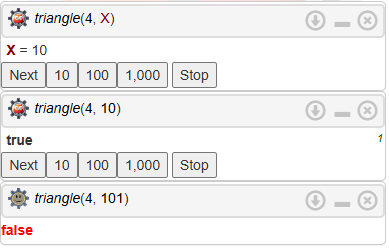
triangle(1, 1).

% Рекурсивный случай

triangle(N, NthTriangle) :-

N > 1,

N1 is N - 1,

triangle(N1, Temp),

NthTriangle is Temp + N.

% Проверяем, что NthTriangle — число, если оно уже задано

%triangle(_, NthTriangle) :-

% nonvar(NthTriangle),

% \+ integer(NthTriangle), !, fail.

%triangle(4, X)

%triangle(4, 10)

%triangle(4, 101)

%2

dot([], [], 0). % Базовый случай: два пустых списка → произведение 0.

dot([H1|T1], [H2|T2], DotProduct) :-

dot(T1, T2, PartialProduct), % Рекурсивно вычисляем произведение хвостов

DotProduct is H1 * H2 + PartialProduct. % Складываем произведения элементов

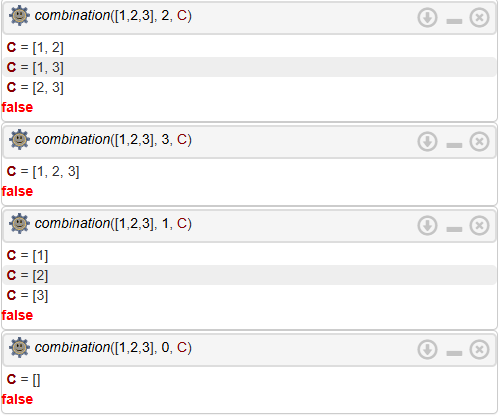
%dot([1,2,3], [4,5,6], Result)

%dot([2,3], [5,7], Result)

/*

dot(List1, List2, _) :-

% Проверяем, что оба списка заданы

(var(List1); var(List2)),

!, fail.

dot(List1, List2, _) :-

% Проверяем, что оба аргумента - списки

(\+ is_list(List1); \+ is_list(List2)),

!, fail.

dot(List1, List2, DotProduct) :-

% Проверяем, что оба списка одной длины

length(List1, N), length(List2, N),

ground(DotProduct), % Если DotProduct уже задан

dot_calc(List1, List2, ComputedDot),

ComputedDot =:= DotProduct, % Проверяем, совпадает ли вычисленное значение с заданным

!.

dot(List1, List2, DotProduct) :-

% Если DotProduct не задан, вычисляем его

length(List1, N), length(List2, N),

dot_calc(List1, List2, DotProduct).

% Базовый случай: пустые списки → произведение 0

dot_calc([], [], 0).

% Рекурсивное вычисление скалярного произведения

dot_calc([H1|T1], [H2|T2], DotProduct) :-

number(H1), number(H2), % Проверяем, что элементы - числа

dot_calc(T1, T2, PartialProduct),

DotProduct is H1 * H2 + PartialProduct.

*/

% Основной предикат для проверки нормальной формы многочлена

polynom(Expr) :-

write('Начинаем проверку: '), write(Expr), nl,

expr_to_terms(Expr, Terms),

write('Слагаемые: '), write(Terms), nl,

check_non_zero_coefficients(Terms),

check_decreasing_degrees(Terms),

write('Многочлен в нормальной форме.'), nl.

% Разбирает выражение в список термов (Коэффициент, Степень)

expr_to_terms(Expr, Terms) :-

split_terms(Expr, RawTerms),

normalize_terms(RawTerms, Terms).

% Разделяет выражение на список термов

split_terms(A + B, Terms) :-

!,

split_terms(A, TermsA),

split_terms(B, TermsB),

append(TermsA, TermsB, Terms).

split_terms(Coeff * x^Power, [(Coeff, Power)]) :- !.

split_terms(x^Power, [(1, Power)]) :- !.

split_terms(Coeff * x, [(Coeff, 1)]) :- !.

split_terms(x, [(1, 1)]) :- !.

split_terms(Coeff, [(Coeff, 0)]) :- number(Coeff), !.

% Сортирует термы по убыванию степени

normalize_terms(Terms, Sorted) :-

predsort(compare_degree, Terms, Sorted).

% Сравнивает степени для сортировки

compare_degree(>, (_, P1), (_, P2)) :- P1 < P2.

compare_degree(<, (_, P1), (_, P2)) :- P1 > P2.

% Проверяет, что нет нулевых коэффициентов

check_non_zero_coefficients([]).

check_non_zero_coefficients([(Coeff, _) | Rest]) :-

Coeff \= 0,

check_non_zero_coefficients(Rest).

% Проверяет, что степени идут по убыванию

check_decreasing_degrees([_]).

check_decreasing_degrees([(_, P1), (_, P2) | Rest]) :-

P1 > P2,

check_decreasing_degrees([(_, P2) | Rest]).

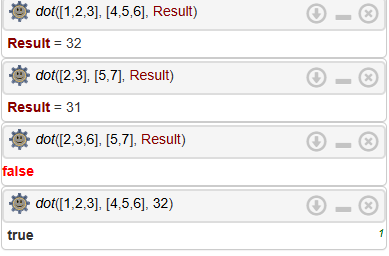
%polynom(2*x^3 + 3*x^2 + x + 2)

%polynom(2*x^3 + x)

%polynom(2*x^3 + x^3)

%polynom(2*x^3 + 3*x^2 + x)

%polynom(2*x^3 + 0*x^2 + x)

%4

combination(_, 0, []).

combination([H|T], K, [H|Comb]) :-

K > 0,

K1 is K - 1,

combination(T, K1, Comb).

combination([_|T], K, Comb) :-

K > 0,

combination(T, K, Comb).

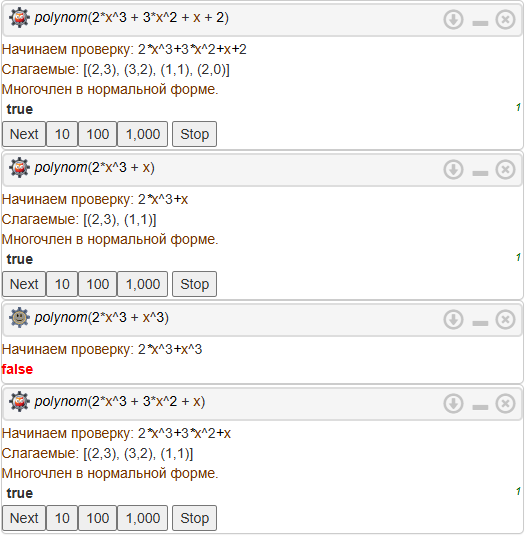
%combination([1,2,3], 2, C)

%combination([1,2,3], 3, C)

%combination([1,2,3], 1, C)

%combination([1,2,3], 0, C)

:- op(500, xfy, ^). % Определяем оператор ^

% Основной предикат

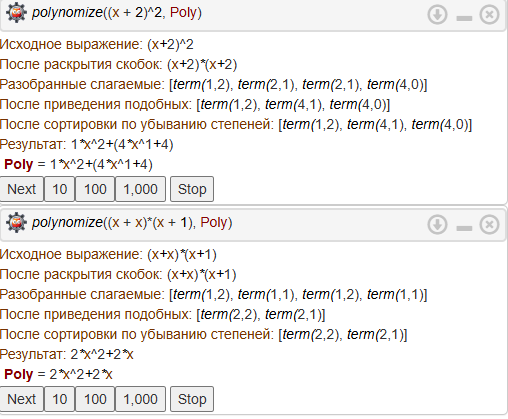
polynomize(Expr, Poly) :-

write('Исходное выражение: '), write(Expr), nl,

expand_expr(Expr, Expanded),

write('После раскрытия скобок: '), write(Expanded), nl,

expr_to_terms(Expanded, Terms),

write('Разобранные слагаемые: '), write(Terms), nl,

combine_like_terms(Terms, Combined),

write('После приведения подобных: '), write(Combined), nl,

sort_terms_by_degree(Combined, Sorted),

write('После сортировки по убыванию степеней: '), write(Sorted), nl,

terms_to_polynomial(Sorted, Poly),

write('Результат: '), write(Poly), nl.

% Раскрытие выражений

expand_expr(A + B, A1 + B1) :- expand_expr(A, A1), expand_expr(B, B1).

expand_expr(A * B, A1 * B1) :- expand_expr(A, A1), expand_expr(B, B1).

expand_expr(A^N, Expanded) :- integer(N), N > 0, expand_power(A, N, Expanded).

expand_expr(A, A).

% Раскрытие степеней

expand_power(A, 1, A).

expand_power(A, N, A * Rest) :-

N > 1, N1 is N - 1, expand_power(A, N1, Rest).

% Преобразование в список слагаемых

expr_to_terms(A + B, Terms) :-

expr_to_terms(A, TermsA),

expr_to_terms(B, TermsB),

append(TermsA, TermsB, Terms).

expr_to_terms(A * B, Terms) :-

expr_to_terms(A, TermsA),

expr_to_terms(B, TermsB),

multiply_terms(TermsA, TermsB, Terms).

expr_to_terms(C*x^P, [term(C, P)]) :- number(C), integer(P).

expr_to_terms(x^P, [term(1, P)]) :- integer(P).

expr_to_terms(C*x, [term(C, 1)]) :- number(C).

expr_to_terms(x, [term(1, 1)]).

expr_to_terms(C, [term(C, 0)]) :- number(C).

% Умножение слагаемых

multiply_terms([], _, []).

multiply_terms(_, [], []).

multiply_terms([term(C1, P1) | T1], T2, Result) :-

multiply_term_with_list(term(C1, P1), T2, Res1),

multiply_terms(T1, T2, Res2),

append(Res1, Res2, Result).

multiply_term_with_list(_, [], []).

multiply_term_with_list(term(C1, P1), [term(C2, P2) | T], [term(C, P) | Rest]) :-

C is C1 * C2,

P is P1 + P2,

multiply_term_with_list(term(C1, P1), T, Rest).

% Приведение подобных

combine_like_terms([], []).

combine_like_terms([term(C, P) | Terms], Combined) :-

select(term(C1, P), Terms, Rest), !,

C2 is C + C1,

( C2 =:= 0 -> combine_like_terms(Rest, Combined)

; combine_like_terms([term(C2, P) | Rest], Combined) ).

combine_like_terms([Term | Terms], [Term | Combined]) :-

combine_like_terms(Terms, Combined).

% Сортировка по убыванию степеней

sort_terms_by_degree(Terms, Sorted) :-

sort(2, @>=, Terms, Sorted).

% Преобразование списка термов в строковое представление

terms_to_polynomial([], 0).

terms_to_polynomial([term(C, 0)], C) :- !.

terms_to_polynomial([term(1, 1)], x) :- !.

terms_to_polynomial([term(C, 1)], C*x) :- !.

terms_to_polynomial([term(1, P)], x^P) :- !.

terms_to_polynomial([term(C, P)], C*x^P) :- !.

terms_to_polynomial([term(C, P) | Rest], Expr) :-

terms_to_polynomial(Rest, RestExpr),

(RestExpr = 0 -> Expr = C*x^P ;

(RestExpr = C2*x^P2 -> Expr = (C*x^P) + (C2*x^P2) ;

Expr = (C*x^P) + RestExpr)).

%polynomize((x + 2)^2, Poly)

%polynomize((x + x)*(x + 1), Poly)