Лаб. 6 ЗИ

Лабораторная работа №6 Алгоритмы генерации и верификации электронной цифровой подписи

Цели работы Изучение алгоритмов генерации и верификации электронной цифровой подписи и приобретение практических навыков их реализации.

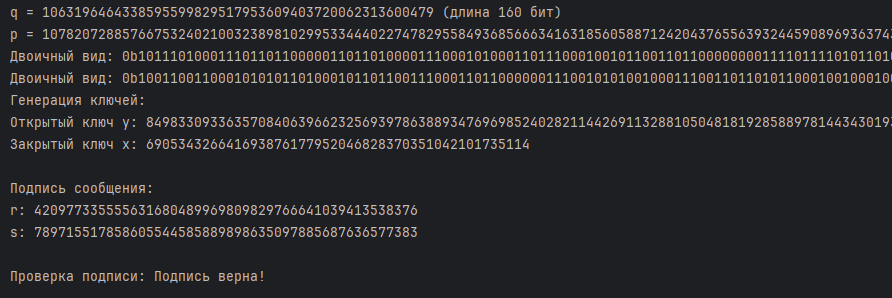
import random from sympy import primerange from sympy import factorint from sympy import nextprime, isprime import time import hashlib import secrets LIMIT = 2000 # Даёт список простых чисел из заданного диапозона PRIMES = list(primerange(1, LIMIT)) # PRIMES = sieve_of_eratosthenes(limit) def generate_number(count_of_checks: int, bit_length: int) -> int: if bit_length <= 64: raise ValueError("bit_length должен быть больше 64") count_of_generate = 0 number = 0 flag = False # Начинаем отсчёт времени start_time = time.perf_counter() while not flag: # Генерируем случайное число из (bit_length - 1) бит и ставим старший бит в 1 number = random.getrandbits(bit_length - 1) | (1 << (bit_length - 1)) # Заменяем младший бит на 2 number |= 1 count_of_generate += 1 if any(number % prime == 0 for prime in PRIMES): continue flag = rabin_miller_test(count_of_checks, number) # Останавливаем отсчёт времени end_time = time.perf_counter() print("Количество генераций большого простого числа: ", count_of_generate) elapsed_time_ms = (end_time - start_time) * 10 ** 3 # в микросекундах print(f"Время генерации: {elapsed_time_ms:.2f} мс") return number def rabin_miller_test(count_of_checks: int, number: int) -> bool: b = 0 m = number - 1 while m % 2 == 0: # Пока делится на 2 m //= 2 # Делим на 2 b += 1 # Увеличиваем b #print("b:", b) #print("m:", m) for _ in range(count_of_checks): a = random.randint(2, number - 1) # Шаг 1 j = 0 z = pow(a, m, number) # Шаг 2 if z == 1 or z == number - 1: # Шаг 3: number проходит тест continue j += 1 while j < b - 1 and z < number - 1: # Шаг 4-5 z = pow(z, 2, number) if z == 1: return False # Число составное if z == number - 1: break j += 1 if z != number - 1: # Шаг 6 return False # Число составное return True # Генерация ключей def generate_keys(): # q = 1 # while q != None: # bit_length = 1024 # count_of_checks = 5 # Количество проверок в тесте Рабина-Миллера # p = generate_number(count_of_checks, bit_length) # # factors = factorint(p - 1) # possible_q = [q for q in factors.keys() if 160 == q.bit_length() and isprime(q)] # # q = possible_q[0] if possible_q else None q = 0 while True: while q.bit_length() != 160: q = nextprime(random.getrandbits(160)) k = random.getrandbits(864) p = k * q + 1 if isprime(p) and p.bit_length() == 1024: break print(f"q = {q} (длина {q.bit_length()} бит)") print(f"p = {p} (длина {p.bit_length()} бит)") print(f"Двоичный вид: {bin(q)}") print(f"Двоичный вид: {bin(p)}") p_ = p - 1 g = 0 while g <= 1: v = random.randint(1, p_ - 1) g = pow(v, p_ // q, p) x = random.randint(1, q - 1) y = pow(g, x, p) print(f"Генерация ключей:\nОткрытый ключ y: {y}\nЗакрытый ключ x: {x}\n") return (p, q, g, x, y) # Функция хеширования (SHA-1) def hash_message(message): hash_object = hashlib.sha1(message.encode()) return int(hash_object.hexdigest(), 16) def sign_message(message, p, q, g, x): H_m = hash_message(message) r = 0 s = 0 while r == 0 or s == 0: #k = random.randint(1, q - 1) k = secrets.randbelow(q) k_inv = pow(k, -1, q) r = pow(g, k, p) % q s = (k_inv * (H_m + x * r)) % q print(f"Подпись сообщения:\nr: {r}\ns: {s}\n") return (r, s) # Верификация подписи def verify_signature(message, r, s, p, q, g, y) -> bool: if not (0 < r < q and 0 < s < q): return False H_m = hash_message(message) s_inv = pow(s, -1, q) u1 = (H_m * s_inv) % q u2 = (r * s_inv) % q v = ((pow(g, u1, p) * pow(y, u2, p)) % p) % q return v == r def main(): # DSA p, q, g, x, y = generate_keys() message = "Hello, world!" r, s = sign_message(message, p, q, g, x) valid = verify_signature(message, r, s, p, q, g, y) print(f"Проверка подписи: {'Подпись верна!' if valid else 'Подпись неверна!'}") if __name__ == "__main__": main()