Лаб. 5 ЗИ

Лабораторная работа №5 Обмен ключами по схеме Диффи-Хеллмана

Цели работы Освоить методы генерации больших простых чисел и методы проверки больших чисел на простоту. Познакомиться с теоремой Эйлера, научиться строить первообразные корни по модулю 𝑛. Изучить схему обмена ключами Диффи-Хеллмана

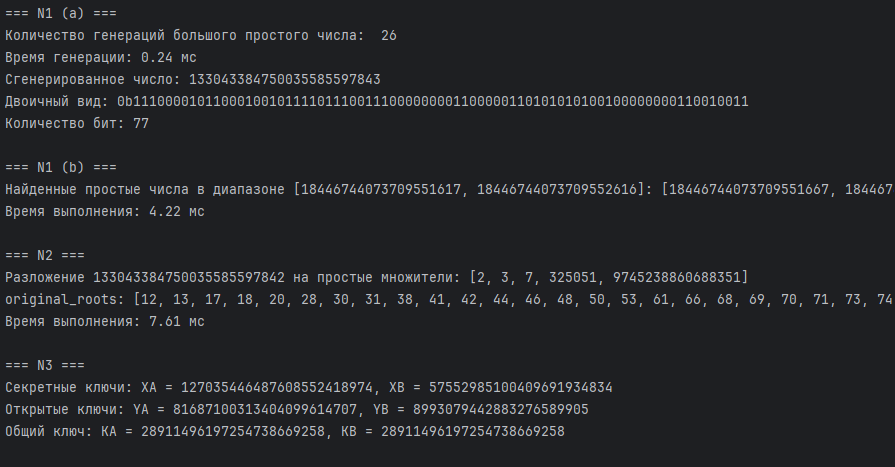
import random from sympy import primerange from sympy import factorint import time # Даёт список простых чисел из заданного диапозона # def sieve_of_eratosthenes(limit): # # Список True, который будет использоваться для маркировки простых чисел # primes = [True] * (limit + 1) # primes[0], primes[1] = False, False # 0 и 1 не простые числа # # for num in range(2, int(limit**0.5) + 1): # if primes[num]: # for multiple in range(num * num, limit + 1, num): # primes[multiple] = False # # # Возвращаем список простых чисел # return [num for num, is_prime in enumerate(primes) if is_prime] # Разложение числа на простые множители # def prime_factorization(n) -> list[int]: # factors = [] # d = 2 # while d * d <= n: # while n % d == 0: # factors.append(d) # n //= d # d += 1 # if n > 1: # factors.append(n) # return factors LIMIT = 2000 # Даёт список простых чисел из заданного диапозона PRIMES = list(primerange(1, LIMIT)) # PRIMES = sieve_of_eratosthenes(limit) def generate_number(count_of_checks: int, bit_length: int) -> int: if bit_length <= 64: raise ValueError("bit_length должен быть больше 64") count_of_generate = 0 number = 0 flag = False # Начинаем отсчёт времени start_time = time.perf_counter() while not flag: # Генерируем случайное число из (bit_length - 1) бит и ставим старший бит в 1 number = random.getrandbits(bit_length - 1) | (1 << (bit_length - 1)) # Заменяем младший бит на 2 number |= 1 count_of_generate += 1 if any(number % prime == 0 for prime in PRIMES): continue flag = rabin_miller_test(count_of_checks, number) # Останавливаем отсчёт времени end_time = time.perf_counter() print("Количество генераций большого простого числа: ", count_of_generate) elapsed_time_ms = (end_time - start_time) * 10 ** 3 # в микросекундах print(f"Время генерации: {elapsed_time_ms:.2f} мс") return number def rabin_miller_test(count_of_checks: int, number: int) -> bool: b = 0 m = number - 1 while m % 2 == 0: # Пока делится на 2 m //= 2 # Делим на 2 b += 1 # Увеличиваем b #print("b:", b) #print("m:", m) for _ in range(count_of_checks): a = random.randint(2, number - 1) # Шаг 1 j = 0 z = pow(a, m, number) # Шаг 2 if z == 1 or z == number - 1: # Шаг 3: number проходит тест continue j += 1 while j < b - 1 and z < number - 1: # Шаг 4-5 z = pow(z, 2, number) if z == 1: return False # Число составное if z == number - 1: break j += 1 if z != number - 1: # Шаг 6 return False # Число составное return True def find_primes_in_range(start: int, end: int, count_of_checks: int) -> None: if start < 2**64: raise ValueError("Нижняя граница должна быть не меньше 2**64") if start % 2 == 0: start += 1 start_time = time.perf_counter() primes = [] # -- for n in range(start, end + 1, 2): # Проверяем только нечётные числа if any(n % prime == 0 for prime in PRIMES): continue # Пропускаем составные числа if rabin_miller_test(count_of_checks, n): primes.append(n) # -- # for n in range(start, end + 1, 6): # Проверяем только числа 6k ± 1 # for candidate in (n, n + 2): # if candidate > end: # break # if any(candidate % prime == 0 for prime in PRIMES): # continue # if rabin_miller_test(count_of_checks, candidate): # primes.append(candidate) end_time = time.perf_counter() elapsed_time_ms = (end_time - start_time) * 10 ** 3 print(f"Найденные простые числа в диапазоне [{start}, {end}]: {primes}") print(f"Время выполнения: {elapsed_time_ms:.2f} мс") def find_original_roots(count_roots: int, number: int) -> list[int]: fi = number - 1 # factors = factorint(fi) # print(f"Разложение {fi} на простые множители: {factors}") primes_list = list(factorint(fi).keys()) print(f"Разложение {fi} на простые множители: {primes_list}") # primes_list = list(set(prime_factorization(fi))) degree_list = [fi // prime for prime in primes_list] original_roots = [] count = 2 start_time = time.perf_counter() while len(original_roots) < count_roots: if all(pow(count, degree, number) != 1 for degree in degree_list): original_roots.append(count) count += 1 end_time = time.perf_counter() elapsed_time_ms = (end_time - start_time) * 10 ** 3 print(f"original_roots: {original_roots}") # print(f"len_original_roots: {len(original_roots)}") print(f"Время выполнения: {elapsed_time_ms:.2f} мс") return original_roots # flag = True # for i in range(len_degree_list): # result_list[i] = pow(count, degree_list[i], number) # if result_list[i] == 1: # count += 1 # flag = False # break # if flag: # original_roots.append(count) # count += 1 # print(f"result_list: {result_list}, count: {count}") # if 1 in result_list: # count += 1 # continue # else: # original_roots.append(count) # count += 1 def diffie_hellman(n: int, g: int) -> None: # Генерирпция случайных секретных ключей XA и XB XA = random.randint(1, n - 1) XB = random.randint(1, n - 1) # Вычисление открытых ключей YA = pow(g, XA, n) YB = pow(g, XB, n) # 3. Вычисляется общий секретный ключ KA = pow(YB, XA, n) KB = pow(YA, XB, n) print(f"Секретные ключи: XA = {XA}, XB = {XB}") print(f"Открытые ключи: YA = {YA}, YB = {YB}") print(f"Общий ключ: KA = {KA}, KB = {KB}") def main(): # 1 (a) print("=== N1 (a) ===") # bit_length = int(input("Введите количество бит (больше 64): ")) # count_of_checks = int(input("Количество проверок в тесте Рабина-Миллера: ")) bit_length = 77 count_of_checks = 5 # Количество проверок в тесте Рабина-Миллера number = generate_number(count_of_checks, bit_length) print(f"Сгенерированное число: {number}") print(f"Двоичный вид: {bin(number)}") print(f"Количество бит: {number.bit_length()}") # rabin_miller_test(129) # 1 (b) print("\n=== N1 (b) ===") start = 2 ** 64 end = 2 ** 64 + 10 ** 3 find_primes_in_range(start, end, count_of_checks) # 2 print("\n=== N2 ===") original_roots = find_original_roots(100, number) # 3 print("\n=== N3 ===") diffie_hellman(number, original_roots[0]) # limit = 2000 # primes = sieve_of_eratosthenes(limit) # print(primes) # primes_sympy = list(primerange(1, limit)) # print(primes_sympy) if __name__ == "__main__": main() # def rabin_miller_test(number: int) -> None: # count_b = 0 # b = 0 # while (number - 1) >= 2**count_b: # if (number - 1) % 2**count_b == 0: # b = count_b # count_b += 1 # # print ("b: ", b)