3 Аппроксимация частотной характеристики рабочего ослабления фильтра
На данном этапе по заданным техническим требованиям к ФНЧ необходимо получить математические выражения передаточной функции Т(р) и рабочего ослабления фильтра A .
Известно, что частотные свойства фильтра определяются функцией фильтрации (1.11):
Следовательно, задача сводится к выбору аналитического выражения этой функции и расчету ее коэффициентов. В качестве аппроксимирующих принято использовать полиномиальные функции, среди которых наиболее широкое применение имеют полиномы Баттерворта и Чебышева.
3.1 Аппроксимация по Чебышеву
При выборе полинома Чебышева в качестве аппроксимирующего функция фильтрации определяется выражением:
,
где ε вычисляется по формуле,
- полином Чебышева, n - порядок полинома
Чебышева (порядок фильтра):
Из (3.10) при n = 1 имеем,
при n = 2
а при n ≥ 3 можно воспользоваться
рекуррентной формулой:
Таким образом, при аппроксимации по
Чебышеву функция рабочего ослабления
имеет вид:
,
которой соответствует графики, показанные
на рис. 3.3. а). Аппроксимация по Чебышеву
получила название равноволновой. Число
экстремумов в ПП, включая граничные
частоты, зависит от технических требований
к фильтру и равно n + 1.
Подобны зависимостям рис.3.3, а в ПП характеристики А(Ω) фильтров Золотарева-Кауэра, имеющие колебательный характер в ПН (рис. 3.3 б), на котором Аs - гарантированное рабочее ослабление в ПН для Ω > Ωs).
Используя в качестве аппроксимирующих функций дроби Чебышева, можем получить характеристику рабочего ослабления А(Ω) фильтра, подобную в ПП характеристике фильтра Баттерворта, а в ПЗ-фильтра Золотарева-Кауэра.
Следует отметить, что аппроксимация по Чебышеву (Золотареву-Кауэру) дает большую крутизну нарастания характеристики рабочего ослабления, чем аппроксимация по Баттерворту (и другим видам, рассмотренным в предыдущем параграфе), проигрывая при этом в линейности фазовой характеристики В(Ω ) (см. рис. 3.3 а) ).
а) б)
Рис.3.2 Характеристики фильтров Чебышева для различного порядка а), характеристика фильтра Золотарёва – Кауэра б).
Оценку линейности В(Ω) удобно производить с помощью группового времени запаздывания (ГВЗ), определяемого первой производной рабочей фазы по частоте:
Зависимости ГВЗ t(Ω) фильтров Баттерворта (1) и Чебышева (2) показаны на рис. 3.3 б). Постоянство t(Ω) свидетельствует о линейности В(Ω). Если В(Ω) - линейна, то t(Ω ) = сonst.
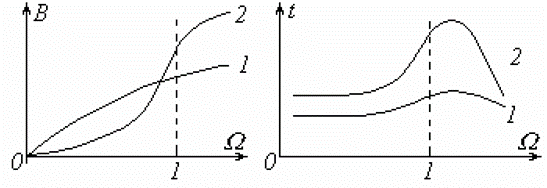
а) б)
Рис.3.3 Характеристика зависимости рабочей фазы а), характеристики зависимости группового времени запаздывания б).
Для формирования рабочей передаточной функции по Чебышеву поступаем аналогично выше изложенному:
,
где
определяется корнями уравнения
,
лежащими в левой полуплоскости:
где
Таким образом,
и искомые функции Т (р) и А(Ω) определяются согласно (3.6)
Расчет 3.1 Выполнить аппроксимацию по Чебышеву рабочей передаточной функции Т (р) и функции рабочего ослабления А(Ω р) для ФНЧ со следующими техническими требованиями: ΔА = 1,3 дБ, f₂ = 7,3 кГц, f₃ = 11,0 кГц, Amin = 27 дБ, R₂ = 150 Ом.
1. Нормируем частоты относительно f2:
2. Расчет коэффициента неравномерности ε:
3. Определение порядка фильтра n
Порядок фильтра для аппроксимации по Чебышеву:
Подставляем значения:
4. Полином Чебышева Pn (Ω)
Для n = 5 используем рекуррентную формулу:
Квадрат модуля функции фильтрации:
5. Расчет корней полинома знаменателя V (p)
Корни pk находятся по формуле:
где
Корни:
6. Формирование передаточной функции T(p)
После раскрытия знаменателя:
7. Проверка рабочего ослабления A(Ω)
На Ω = 0:
На Ω=1:
На Ω=1,5068:
Рис. 3.4 Характеристика аппроксимации по Чебышеву для ФНЧ