РАЗДЕЛ 4 ОСНОВНАЯ ЧАСТЬ

4.1ТЕОРЕТИЧЕСКАЯ ЧАСТЬ

НСП (аналогично ДСП) предполагает изменение состояния систем (переход из состояния в состояние) в определенные моменты времени, при этом моменты времени или события определены стохастически и заданы непрерывным законом распределения случайной величины. При описании входного потока с использованием пуассоновского распределения (пуассоновское распределение описывает вероятность того, что в течение

описывает экспоненциальное распределение.

Кроме того, при НСП непрерывными законами распределения описывается обработка поступающей информации.

Область применения НСП аналогична ДСП, но фокус моделирования смещён в сторону исследования временных затрат, задержек, простоев.

35

4.2ПОСТАНОВКА ЗАДАЧИ ИССЛЕДОВАНИЯ

На основе исходных данных модели из 3 раздела необходимо сделать следующее:

Полученный входной поток должен быть обработан определённым ранее оптимальным количеством процессоров в соответствии с распределением Кокса. Распределение содержит число фаз, равное числу процессоров, равновероятное, продолжительность каждой фазы - 9 миллисекунд, умноженный на номер фазы.

Каждая фаза обслуживания привязана к своему процессору.

36

4.3ПРОВЕДЕНИЕ МОДЕЛИРОВАНИЯ

Размер каждого буфера неограничен. Возможная отрицательность размера буфера обусловлена тем, что таким образом можно видеть тенденцию работу модели: убывает ли сумма размеров буферов или возрастает.

Модель из раздела 3 курсовой работы была модифицирована следующим образом: был добавлен модуль задержки – фаза для каждого канала в количество одной штуки ( ). Модуль-получатель, он же буфер без ограничения, был оставлен нетронутым.

37

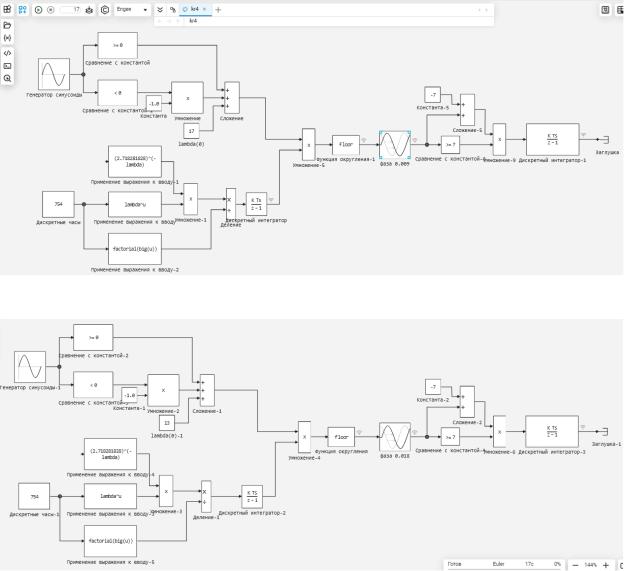
Таким образом была получена следующая модель (рисунок 28а, 28б):

Рисунок 28а. Модель для раздела 4 курсовой работы (верхняя часть)

Рисунок 28б. Модель для раздела 4 курсовой работы (нижняя часть)

38

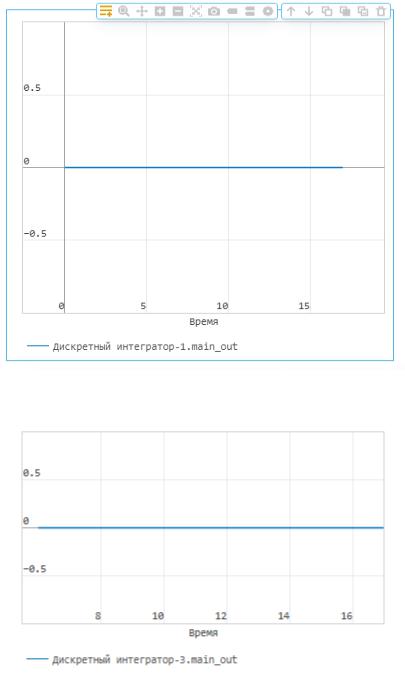
( ) Добавление лишь одной фазы объясняется тем, что за время моделирования системы из третьего раздела (17 секунд) размеры выходного буфера как первого, так и второго каналов остаются неизменными и равны нулю (кроме последнего такта первого канала; в данном случае на последнем такте равно единице) (рисунок 29а, рисунок 29б). Это, в свою очередь, означает, что выходного потока достаточно, чтобы система отрабатывала без «остатка»

Рисунок 29а. Состояние выходного буфера первого канала в течение 17с

Рисунок 29б. Состояние выходного буфера второго канала в течение 17с 39

Модель делится на три части:

1.Дискретизация синусоиды

2.Функция распределения Пуассона

3.Узел-получатель

При этом стоит отметить, что частота синусоидального сигнала равна 3 радиана в секунду. Время работы модели – 17 секунд.

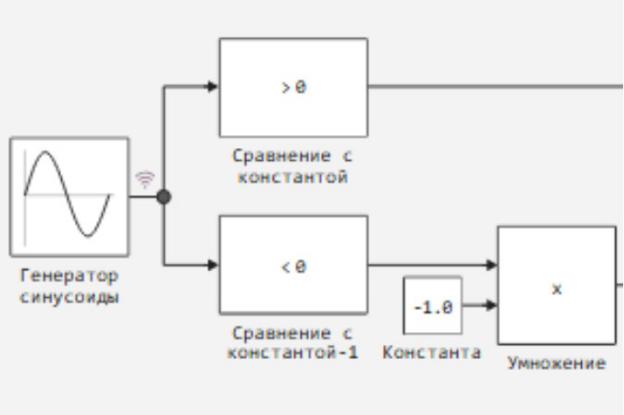
Первая часть:

Рисунок 30. Дискретизация сигнала генератора sin

В данном случае не идет сравнение с нулем, поскольку функция непрерывна и ее график все−1равно проходит через значение равное нулю. Домножение на константу при значении меньше нуля нужно, поскольку оператор сравнения – булевый.

40

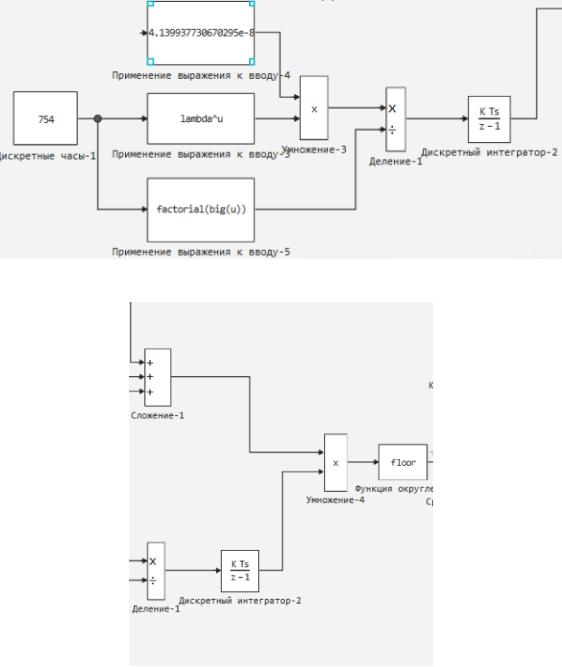
Вторая часть:

Далее происходит вычисление функции распределения Пуассона (рисунок 31) и последующее умножение полученного числа на значение из дискретизатора с дальнейшем округлением (рисунок 32). В данной модели дискретныечасы– значение изформулыПуассона.Соответствующийвыбор сделан из-за того, что данное значение требуется «прогнать» через модель в диапазоне от 0 до 17. Время работы модели как раз таки 17 секунд.

Рисунок 31. Вычисление функции распределения Пуассона

Рисунок 32. Умножение. 41

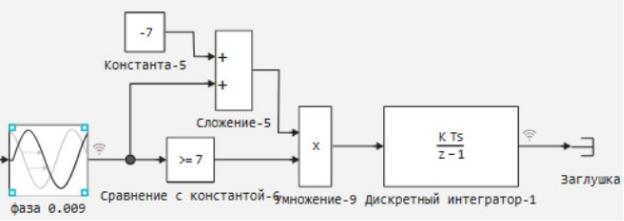
Третья часть:

В самом начале данной части системы находится модуль транспортной задержки, выполняющий роль фазы. Данная задержка равна 9мс в первом канале и 18мс во втором. В каждом канале используется всего одна фаза, поскольку процессор всего один (см. ( )). Всего фаз в модели – две.

Затем( ) происходит «очистка» буфера: из него вычитается значение равное (рисунок 33). В данном случае это значение равно семи. Тем самым симулируется узел-получатель. Дискретный интегратор в конце требуется для получения текущего состояния буфера.

Рисунок 33. Третья часть системы Тем самым, поставив метку лога, можно легко отслеживать поведение( )

буфера:еслифункциявозрастает,тоэтоозначает,чтопослевыхода битов из системы, какая-то их часть остается в буфере и эта часть начинает со временем расти.

42