Лекции, Простокишин В.М. / ДиИУ_7_Квазилинейные_уравнения_Л_07
.pdf
171 9,60%" +... +an60910 |
Ш |
|||
dice |
= m² |
=. = |
М" |
(2) Хд..., %) |
а,(1) |
9260 |
|
9, (2) |
|
1=0, (Х,...., In)
129
Infantile,..., In)
Т •Зих)-решениеур-ния вчастных производных(1), хм...., x.lt)-все характеристики, т
.е
.решения системы ОДУ (2), тогда и(hit...., inch) =cont, to и обратно: Mitt,..., anti)-первый интеграл системы (2), тогда решение ур-ния (1)-ива...,Хи)
первый интеграл исп., хы)для (2) естьрешение а)
Пхд+удушаю
Х-х
g-y 4- chef
1=2 |
¾" два первых интеграла |
|
label-внуквид/ |
||
¥12' |
системы ОДУ |
|
butyl-lula-lull
решения по т.: идти-¥ -решение ур-ния в
частныхпр-ных
• Зп-1: Рту)драку)дую
тогда -решение:
Х-_Ржу)
j-any, yan-yet)s ИИНУ): ИGets,yet)), to
y A |
|
4 |
« |
> Х
.]выполнены основные положения(условияпрошлойтеоремы) и задано (п-1) первых интегралов системы (2):
4111=4,..., Ил-ка-Си-1
I He.....tn,)-произвольнаяф-ня С'(Я,), то
если и
ф-ня и = На...., Сп-е) = Жан, да)...., 4-169)-решение ур-ния,
рассмотрим ди n-и д
Охк =,=, овдт,подставил в 4)
Ёжики-Ё.актив!!!!-Ё.акад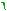
: 
◦
И-решение (1) |
|
◦ по прошлой |
|
теореме |
|
|
|
≠ |
0.am первые интегралы из прошлитеоремы такие, что |
||
|
104 |
0 |
04 |
02 |
0km1 |
Якобианд)ДДваа......."":#↑ |
|
"#внк-ой |
д-, И-1...Мы-1 012 012 dm-1
точке Х:(х,
°....,НЕЯ", то для решений и-ира,...,а)для (е)
7Mt....tn-1)EC'(009 и верно равенство:
некая окрестность Х:(х,9.99
ИВАШИН),.., 4m69)
без доказательства
• прошлая теорема означает,что решениеа)выра |
|||||||
жается как суперпозиция независимых I-хинтегралов |
|||||||
системы ОДУдля характеристик с помощью некоторой |
|||||||
ф-ни#'(0019 |
|
|
|
|
|||
Пример хдд +удую ¼, dey |
1--4 |
|
|
||||
тогда |
|
|
интеграл системы |
||||
|
Иу)-Жд)-произвольная |
||||||
|
|
ф-ня 01001) |
|
|
|
||
Нахождение частногорешения |
|
|
|
||||
Ёакыдко |
|
|
|
ДУу#ц) |
|||
К 1 |
|
|
|
|
(Нац |
||
рассмотрим и-2: Рыу)Д- + Иуду-0, где |
|||||||
задача |
|||||||
P, GEC'N) |
|
|
|
||||
|
|
|
|
Кони |
|||
Гру)+ аду)7062 |
|
|
|
|
|||
|
--Play) Кру, =Ктр |
|
|
|
|||
|
у_ану) |
|
|
|
|
|
|
вину условий выполнена ТЕрешениязкошидля |
|||||||
|
|
т.е. через точку(х,уж'проходит |
ОДУ |
||||
решение: |
( |
единственнаяфазоваякривая) |
|||||
Ижицу)), где |
жхА),у-yet, |
|
|
||||
|
447)-I интеграл |
и |
ИЩУ) |
|
|
||
ура,да)-С,#to hit |
|
|
|||||
|
|
|
|||||
4- Mount |
|
r |
характеристики |
||||
|
|
|
|||||
|
|
|
|
Х |
|
|
|
так задаём некую кривую р, не совпадающую схарактеристикой
Uy)) 
"(ц)„укр-непрерывно-диф-на
получаем рад, + аду
Mayer-h""Mayer
(ТЕрешения)
• з задана рна Оку,не касающаяся характеристикии), аф-ня hey)Edвнек-ой окр-сти з, тогда заданазадача
Коми для ур-ния по + аду-о и она имеет!решение
внек-ой окр-ти р без доказательства#
Пример-удудую, найтирешение, проходящее через
1) 8: 4х-0, и-43
=-у I-х
dutydy-0 |
И-44743 |
47C
МУЖ.-у" Круг
Mtb
-
ихну" А!решение
2) Р: {12+2-1,4-1}
""Н„ут жу?)„тут-1 Г=характеристика
!решение выделить невозможно
Квазилинейныеуравнения вчастных производных
•К»ак (х,4)драки), |
(1) (неизвестная ф-ня и входит |
|
в обе части ул-ния) |
где ак, КП и а. ЕС"(А"") или ECIGXRI.ge |
|
Ё. айпи)» в R"" |
условия GER", Хед |
сопоставим а) с линейным однороднымур-нием:
Ёлкин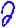 
к + а.инди-0, гении) и
[ДУ существованиярешения)
.]v-жижа")иявляетсярешением к), предполо жим, что ур-ние мам)-0 определяет внекой области да"непрерывно-диф-муюф-ню и-инжира....-х") и
, тогда и-их)-решениеул-ния(1)
4=4(Х)
рассмотрим их,47=0, определяющуюиМедея"), тогда по т. о неявнойф-ни запишем сучётом *^
ди |
Маск , подставил: |
ONE |
ON/ди |
[акции,1- Мак) =-да
04 (Хи) к акк1449%46,4)-
К-1
|
Д) -а.(хит), т.е. получили:Ёаккиндкана |
|
% (ход |
К/ над |
|
Фон |
|
|
|
|
|
(2) |
тогда и-исх)-решениеурения в |
|
частных производныхи) |
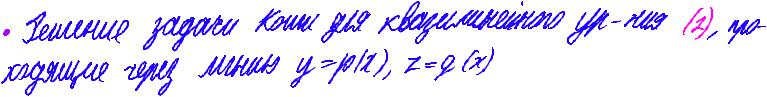
• решение задачи кожидля квазилинейногоул-ния (2), про ходящие через мышь у-ры), z-да)