
Лекции, Простокишин В.М. / Электронный формат / ДиИУ_1_Элементы_теории_устойчивости_Л_01
.pdf
Дифференциальные и интегральные уравнения (ДиИУ)
Л.01
Глава 1. Теория устойчивости решений систем ОДУ
1.1. Основные определения
Рассмотрим систему ОДУ вида |
|
|
|||||||
|
|
1 |
|
= ( , |
, … , |
) |
|
|
|
|
|
|
1 |
(0) = 10 |
|||||
(1) |
|
1 |
1 |
|
|
||||
|
|
|
|
… |
|
с начальными условиями вида |
(2) { |
… |
|
|
|
|
|
|
|
||||
|
|
|
|
= ( , |
, … , |
) |
|
(0) = 0 |
|
|
|
|
|
||||||
|
{ |
2 |
1 |
|
|
|
|
||
|
|
|
|
|
|
|
|
||
Коротко будем записывать эту задачу Коши в векторном виде:
|
|
= ( , ) |
где = ( , … , ) , |
= ( , … , ) , |
= (0, … , 0) |
(К1) |
|
||||||||
|
|
||||||||||||||
|
|
|
|
1 |
|
|
|
1 |
|
0 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
(0) = 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( , ) = ( ( , |
, … , |
), ( , |
, … , |
), … , ( , |
, … , )) ([0, +∞) х |
→ |
– заданная функция |
|||||||
1 |
1 |
|
2 1 |
|
|
1 |
|
|
|
|
|
|
|
||
|
в частности это – непрерывная функция ( , ) [0, +∞) х |
→ |
|
|
|
|
|
||||||||
Основное предположение: задача (К1) имеет единственное классическое решение для 0 |
|
( – область), |
|||||||||||||
(решение задачи Коши (К1) существует, единственно и определено при всех [0, +∞), например, ( , ) непрерывна на
|
и удовлетворяет условию Липшица по |
|
) т.е. |
|
! набор функций (t), непрерывно дифференцируемых |
[0, +∞) х |
|
|
при ≥ 0, который при подстановке в (К1) обращает эту задачу в тождественную.
Ранее была доказаны теоремы о существовании и единственности решения и о непрерывной зависимости решения от начальных данных для системы (1). Решение задачи Коши с немного «возмущенными» начальными данными «не сильно» отличалось от решения «невозмущенной» задачи Коши при [0, ]. Нас в данном рассмотрении будет интересовать случай, когда [0, +∞) .
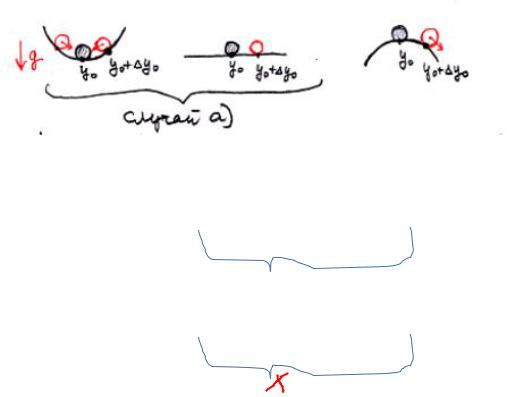
Решение задачи (К1) зависит от и от 0: = ( ; 0). |
|
||
Возьмем вместо 0 |
другое начальное условие: 0 + ∆0, где ∆0 – 'мало’, т.е. 0 и 0 + ∆0 – ‘близки’ (что это см. ниже). |
||
Найдем решение системы (1) для этого начального условия: = ( ; 0 + ∆0). |
|||
Логически возможны два случая: |
|
|
|
а) при ‘малых’ ∆0 |
решение ( ; 0 + ∆0) ‘близко’ к решению |
( ; 0) при ≥ 0 ; |
|
б) при ‘малых’ ∆ |
решение ( ; |
+ ∆ ) может отличаться от |
( ; ) сколь угодно велико (по крайней мере при ≥ ) |
0 |
0 |
0 |
0 |
Эти случаи качественно можно проиллюстрировать физическим примером.
Движение шарика описывается системой ОДУ.
Иллюстрация рассматриваемых понятий на простом примере задачи Коши для ОДУ: |
{ |
/ = |
( ) = 0 |
|
||||||||||||||
|
|
|||||||||||||||||
(0) = 0 |
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
а.1) параметр < 0 |
( ; |
+ ∆ ) − ( ; |
) = ( |
+ ∆ |
) |
− = ∆ = ∆ −| | |
|
|
||||||||||
|
|
|
|
0 |
|
0 |
0 |
|
0 |
0 |
|
0 |
0 |
|
0 |
|
|
|
|
∆ |
, |∆ | < |
|( ; |
+ ∆ |
) − ( ; )| < −| | |
≤ |
≥ 0 |
|
|
|
|
|
|
|||||
|
0 |
0 |
|
|
0 |
0 |
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
→0 при → +∞ |
|
|
|
|
|
|
|
|
|
|||
а.2) параметр = 0 |
( ; 0 |
+ ∆0) − ( ; 0) = ∆ |
|
|
|
|
|
|
|
|
|
|||||||
|
∆0 , |∆0| < |
|( ; 0 |
+ ∆0) − ( ; 0)| < > 0 |
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
→0 при → +∞ |
|
|
|
|
|
|
|
|
|
|||
б) |
параметр > 0 |
|
|( ; |
+ ∆ ) |
− ( ; |
|
)| = |∆ | |
→ +∞ при → +∞ для ∆ |
≠ 0 |
|
|
|||||||
|
|
|
|
0 |
|
0 |
0 |
|
0 |
|
|
|
|
0 |
|
|
|
|
Вслучаях а.1) и а.2) говорят, что решение задачи устойчиво (по отношению к малым возмущениям начальных условий задачи Коши).
Вслучае б) – решение неустойчиво.
Основания теории устойчивости разработаны А.М. Ляпуновым (конец XIX – начало XX века).
Дадим точные определения. |
|
|
|
|
|
|
|
|
|
|
|
Для оценки ‘малости’ вектора = ( , … , ) будем использовать его норму: ‖ ‖ = √2 |
+ 2 |
+ + 2. |
|||
1 |
|
1 |
2 |
|
|
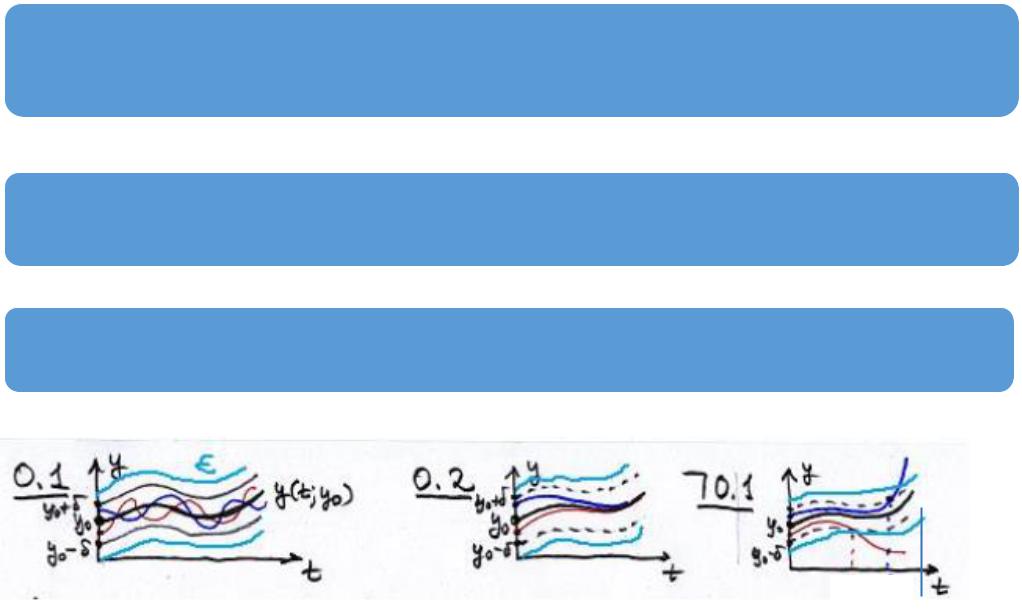
Определение О.1. Решение ( ) = ( ; 0) задачи (К1) называется устойчивым по Ляпунову (или по отношению к
малым изменениям начальных условий), если |
|
|
> 0 0( ) > 0 такое, что ∆ 0 |
|
‖∆ 0‖ < 0( ) и > 0 |
решение ( ; 0 + ∆ 0) лежит в области (0, +∞)х и выполняется неравенство: ‖ ( ; 0 + ∆ 0) − ( ; 0)‖ <
Далее для краткости фразу «решение лежит в области (0, +∞)х » будем опускать, как очевидное требование в контексте.
Определение О.2. Решение ( ) = ( ; 0) задачи (К1) называется асимптотически устойчивым если:
1) оно устойчиво по Ляпунову
2) |
> 0 такое, что при |
∆ 0 ‖∆ 0‖ < 1 |
lim ‖ ( ; 0 + ∆ 0) − ( ; 0)‖ = 0 |
|
1 |
|
→+∞ |
|
|
|
Определение О.3 ( ┐О1). Решение ( ) = ( ; 0)
> 0 что > 0 |
∆ 0 ‖∆ 0‖ < и |
|
|
задачи (К1) называется неустойчивым по Ляпунову
> 0 для которых ‖ ( ; 0 + ∆ 0) − ( ; 0)‖ ≥
Геометрическая иллюстрация.
t*

Математически удобно свести исследование решений задачи (К1) на устойчивость по Ляпунову к некоторому стандартному виду. Для этого введем в (К1) новое неизвестное ( ) = ( ) − ( ; 0) и тогда ( ) = ( ) + ( ; 0) . Здесь ( ) – любое решение системы (1), ( ; 0) – решение задачи Коши (К1) с начальным условием (2) 0 для системы ОДУ (1).
Тогда
|
|
|
|
|
|
|
|
= ( , ), |
( , 0) |
= ( , ( , )), |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
(3) |
|
|
= |
|
− |
(, 0) |
= |
(, ) − (, (, |
)) = (, Х + (, |
)) − (, (, |
)) = (, ) |
|||
|
|
|
|
||||||||||
{ |
|
|
|
0 |
0 |
0 |
|
||||||
|
|
|
|
|
|
||||||||
(0) = (0) − 0 = 0
Получили задачу Коши, относительно неизвестной с новой правой частью (, )
(4) Х = ( , ) Х(0) = Х0
Эта задача отличается тем, что она имеет при 0 = О, решение ( ) = О:
если Х0 = О , то (0) = 0 ( ) = (, 0) ( ) = О и
и новым начальным условием:
(К2)
( , ) = О.
Определение О4. Решение системы ОДУ Х
= ( , ) такое, что ( ) = О (правая часть нулевая) и
( , О) = |
Х |
= О называется «положением равновесия» («точкой покоя») этой системы. |
|
|
|||
|
|
Исследование на устойчивость решения задачи Коши (К1) сводится к исследованию на устойчивость нулевого (тривиального) решения связанной с ней задачи (К2).
Другими словами: исследование решений системы (1) на устойчивость сводится к исследованию точек покоя новой системы (4).

{ 1( ) = − 2 – решение системы.
2( ) =
Сведем систему к новой (с точкой покоя в точке (0, 0) ):
Обоснованием этого служит теорема: |
|
Теорема 1. Решение ( ; 0) задачи Коши (К1) устойчиво (асимптотически устойчиво) тогда и только тогда, когда |
|
устойчиво (асимптотически устойчиво) тривиальное решение ( ) ≡ О (положение равновесия 0 = О) системы |
|
Х̇= ( , ), |
(4) |
где (, ) = ( , Х + (, 0)) − ( , (, 0))
Доказательство. 1. Общие соображения: связь между решениями задач Коши (К1) и (К2) мы показали ранее – (3), при этом начальное условие для (К2): (0) = (0) − 0 . В частности, решению (, 0) задачи Коши (К1) соответствует решение ( ) ≡ О с начальным условием (как мы уже отметили) 0 = О. При этом в силу построения ( , ) очевидно, что( , О) ≡ О , т.е. = О – положение равновесия системы (4).
Итак, решение ( ; 0) задачи Коши (К1) соответствует положение равновесия = О системы (4).
2.Докажем теорему 1 в случае исследования решения на устойчивость по Ляпунову (случай асимптотической устойчивости рассматривается аналогично).
Необходимость. Пусть решение ( ; 0) задачи (К1) устойчиво по Ляпунову. Это означает, что
> 0 ( ) > 0 такое, что ∆0 ‖∆0‖ < ( ) и > 0 решение (; 0 + ∆0)
области (0, +∞)х и выполняется неравенство: ‖ (; 0 + ∆0) − ( ; 0)‖ < .
При переходе к системе (4) это означает, что при тех же ∆0 и всех > 0 ‖ (; ∆0) − О‖ <
следовательно, решение ( ) ≡ О задачи (К2) является устойчивым по Ляпунову. Достаточность утверждения теоремы доказывается аналогично. □
лежит в
, а,
Следствие. Исследование на устойчивость произвольного решения системы (1) сводится к исследованию на устойчивость решения ( ) ≡ О системы (4) , для которой = О является точкой покоя.
В дальнейшем будем исследовать только точки покоя систем ОДУ. Для этого есть набор стандартных методов.
Переформулируем основные определения с учетом введенного понятия «точки покоя» («положения равновесия»).
О.1’. Точка покоя систему ОДУ (4) устойчива по Ляпунову, если
> 0
0( ) > 0 такое, что 0 , ‖ 0‖ < 0( ) и > 0 ‖ ( ; 0)‖ < .
О.2’. Точка покоя систему ОДУ (3) асимптотически устойчива если она: 1) устойчива по Ляпунову
2) |
> 0 такое, что при 0 |
‖ 0‖ < 1 |
lim ‖ ( ; 0)‖ = 0. |
|
1 |
|
→+∞ |
|
|
|
Основные простейшие понятия при анализе устойчивости и неустойчивости точек покоя систем ОДУ можно изучить, рассматривая случае n=2 (система из двух ОДУ).
Решение в параметрическом виде |
x x(t) |
, |
y y(t) |
, |
|
|
«фазовой плоскости» xOy для различных начальных условий.
|
|
|
|
|
|
|
|
|
|
x f1 (t; x, y) |
x x(t) |
|||
|
|
|
|
|
|
|
|
y y(t) |
|
y f |
2 |
(t; x, y) |
||
|
|
|
|
|
t 0
удобно изображать в виде «фазовых портретов» на
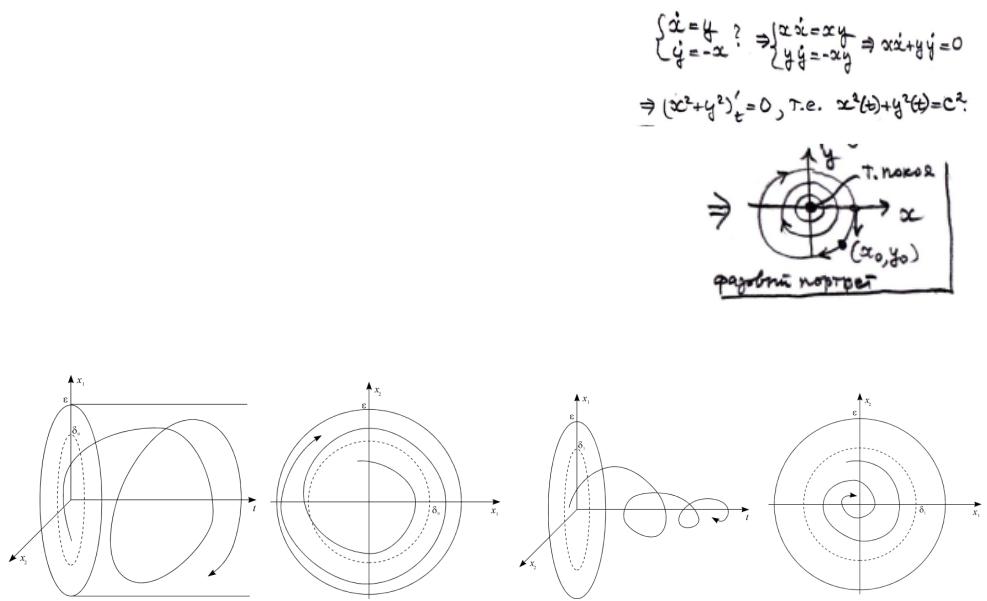
О поведении фазовых траекторий можно судить непосредственно из системы ОДУ, но для этого может потребоваться провести некоторые преобразования.
Например, для системы
|
|
|
|
||
x y |
||
|
|
|
|
||
|
||
y x |
||
можно провести следующие преобразования:
Т.е. в данном случае «фазовые траектории»
(решения системы в параметрическом виде) – концентрические окружности
! подумайте о направлении стрелок на траекториях на рисунке
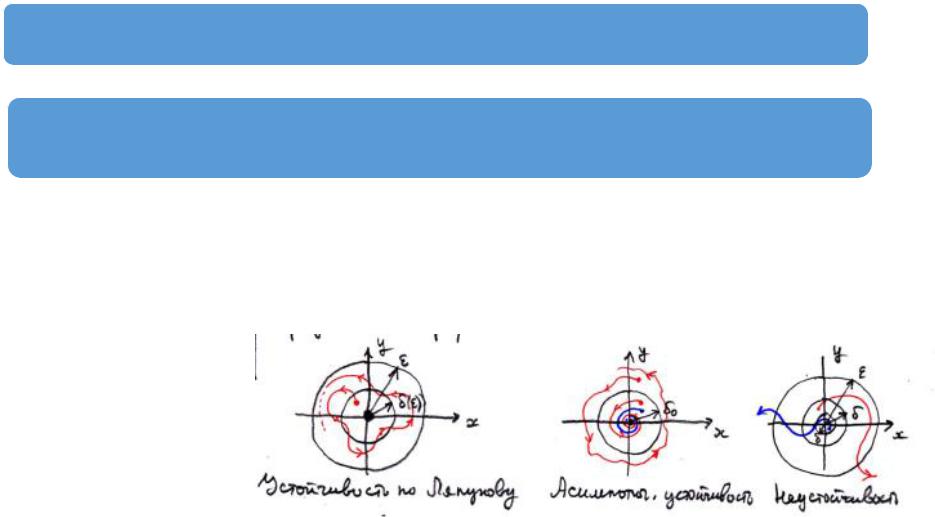
Геометрическая интерпретация определений О.1’ и О.2’ .
Устойчивость по Ляпунову |
Асимптотическая устойчивость |
||
в терминах |
в терминах |
в терминах |
в терминах |
интегральной кривой |
фазовой траектории |
интегральной кривой |
фазовой траектории |
