
Анмех лекции 2025 Барабанов / АМ_14_Метод_Гамильтона_Якоби_Л_14
.pdf
11 Ф

 скобки Пуассона.Метод
скобки Пуассона.Метод
Гамильтона-Якоби. Теорема Лиувилля и адиабатические инварианты
• напоминание
Hq,p.tt?hpi4-119Mt/qscent,
g• .tt,
Pi =-де 15
др) (A, R), НИ.pt/→НАДА
-свойства каноническом пр-ния 1)каждому пр-нию соответствует своя производя.
щая Ф-ка:79: Ё.piai-H-E.BG-44dL-фm-нячая
2)при имеющемся преобразовании к-кое пр-ние
объём фазового пр-ва: Г--Idgaf" Г'=/dad, r
 '
'
= |
-846,14 |
3)17 Alg,p.tlAIQlq.pt),Ala.pt),+) |
|
физ-кая |
физ-кая |
величина |
величина |
в старых |
в новых переменных |
переменных
др {A.'В}ак-инвариантность скобок |
|
{А. Ввт {А:B' |
Пуассона отн-но каноничес |
|
|
|
кого преобразования |

0{Qi, Q;}ар = {Qi, в}др
{E, Pj}• = {Ri,Двр-0
{Pi, Aj} a = {Pi, Q;}95 dig 

скобки Пуассона
Строгое доказательство инвариантностифундамен-
тальных скобок Пуассона
677*91=-7: Aj |
Aj |
|
|
Фк |
- дак |
|
|
→ |
|
|
- ΣPlimpton, |
Haitian =Ё.6934-97171 к Одк а; |
||
+ %df.fdila.pt |
a. |
|
At |
ago |
|
2) EPI,Д-Здр-аналогичнод(1) |
091 |
|
|
|
Aj |
Щ
- ДА-да.
3) ЕР: А-Зар-Ё, 0£!Я# дак Фк =.Eli.tk:676?bfE
= dig
• своегорода, это свойство-условие для канонического преобразования

Метод Гамильтона-Якоби
• зэнезамкнутая система с 5 степенями свободы: H(g.pt), Ндр) →(A,R)
79919,44, 9--Ё.Fitbit 919ft)
sp.at?fgi
Ё-pig:-На.pt/--EIi-Ha.P.t)-EiDiG,-≤.
+ Eth! 17
Р:-91914 |
|
09: |
Р:-89,91, |
Qi-919,445=15 |
|
др |
9: |
HIQ.IT/=Hlq,p.t)-919,4) |
|
|
|
А |
|
• метод заключается в выборе G так, чтобы Но, |
||
тогда Qi-ft#i=o.top -sE=Biai-di--contdiubi.i-ts |
||
Ё |
cont |
берутся из началь |
|
ных условий |
|
:p,-= в 9.10 > д-gilt, ВЫ
дд:
4=99,10 P: =p:ДВА
В:
• ] начальные условия: 9127191г |
...-952 |
рН)= (Рн.... |
/Psr) |

в итоге получаем: |
|
|
|
|
|
|
919, B,t) есть решение ур-ния: |
|
|
|
|||
""""+4191,-95,921.115.1=0-уравнение |
||||||
д- |
|
|
|
Гамильтона-Якоби |
||
• AGlq.B.tl, в |
|
|
|
|
-Н =L-ф-ия |
|
at-Ё. 9gitff-E.pk |
|
Лагранжа |
||||
|
и |
w |
|
|
|
|
+ |
|
|
|
|
||
Pi |
-И |
|
|
|
|
|
Glq.B.ttShalt-5A)-действие по истиннойтраект. |
||||||
и |
|
мы с моментач вточке дрдо |
||||
|
момента + вget) |
|
||||
1,g1e),plz7mкант-met,getl,pct-кое (движение во времени) CGC9.PH/--Sct) |
||||||
|
|
|
) |
|
|
|
|
|
|
|
|
|
|
(Лиувилля) |
|
|
|
|
|
|
при аноничности перехода |
|
|
|
|||
дел,ры |
gets,pct) |
по в-by (2): |
|
|||
|
|
rn-fdpdg.FIdidnt |
||||
Адиабатные инварианты |
|
|
|
|
||
Пример одномерноедвижение вme Va) |
|
|||||
Т Invest-E-unit plan± 2mЕV91 |
|
|||||
|
|
V9) |
pA |
|
1) |
|
|
|
|
|
|
|
|


 peg)
peg)



Я |
2 |
9 |
92 |
2g |
I |
|
|
||
|
|
|
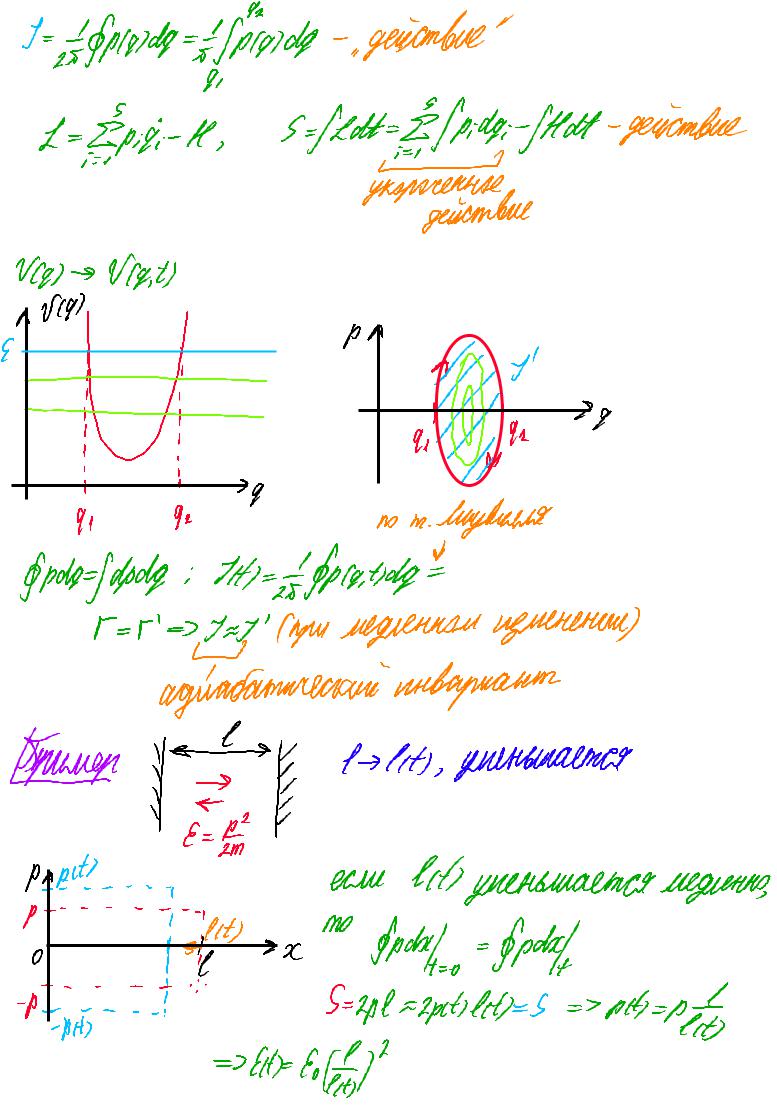
%
1-than-1mm-„действие"
1-Espi.-Н, S-flatt-EIP.dk/Hdt-действие
|
|
укороченное |
|
|
|
действие |
|
V9) → Nat) |
|
|
|
VIN |
|
pA |
|
|
|
1' |
|
|
|
|
|
|
|
91 |
2 |
|
|
|
|
|
|
>q |
|
91 |
92 |
по т-Лиувилля |
|
fpda-fdpdg.int/=,tfpcatidgE
Г-Г' 77'(при медленном изменении)
|
Адиабатический инвариант |
||
Пример |
l |
1- ¼), уменьшается |
|
→ |
|||
|
|
||
|
8 |
|
|
ЕЁ
Р pct) |
если lit'уменьшаетсямедленно, |
: |
e4) 25 Apart.-§pal |
-pA) |
5-Lpl-2pct,lifts pct,=pД) |
|
|
|
* Е.⅓" |
